三大统计学派推断思想的比较研究——以贝伦斯—费歇尔问题为例
2011-07-20朱春浩王文平
朱春浩 王文平
(武汉船舶职业技术学院,湖北武汉 430050)
1 贝伦斯-费歇尔问题
众所周知,统计学中存在三大学派,即奈曼经典学派(或频率学派)、贝叶斯学派、费歇尔信念学派。这三大学派由于其在统计哲学方面的分歧,使得它们对几乎所有的统计问题都有自己的一套解决方法。奈曼置信理论与非置信理论争论最多也最引人注意的就是两均值之差区间估计和检验问题。
1929年,贝伦斯(Behrens)基于工程实践的需要,提出了以下问题:对均值为 μ1,方差为的正态总体X取得了大小为n1的完全样本X1,X2,…,对另一均值为 μ2,方差为的正态总体Y取得了大小为n2的完全样本Y1,Y2,…,Yn2,并且此两个样本相互独立 。在 μ1、μ2、、均未知时,要求根据样本给出δ=μ1-μ2的精确区间估计或假设检验 H0:μ1=μ2,H1:μ1≠μ2。它有三种问题:①μ1=μ2,=。 ②μ1=μ2,假定=(公共值未知)。 ③μ1=μ2。
问题①奈曼、爱根◦皮尔逊在1930年文章《关于两样本检验》中讨论过,他们求得了似然比检验,但对其性质未作深入讨论。
问题②已由费歇尔在1925年文章《Student t分布的应用》中讨论过,他引进了沿用至今的两样本检验,但也没能仔细探究其表现,特别是在作为出发点的假定=不对时,会有如何的后果。
问题③首先由著名的统计学界泰斗费歇尔(R.A.Fisher,1890-1962)进行了研究,所以称为贝伦斯-费歇尔问题。贝伦斯-费歇尔问题应用意义非常重要,例如可应用于空间飞行器性能参数的地面试验与飞行试验的天地差分析、航天产品在不同试验条件的试验参数对比分析等。
许宝騄于1938年在奈曼和爱根◦皮尔逊《统计研究报告》的第2卷发表了关于数理统计学的第一篇论文《Student t分布理论应用于两样本问题》[1],研究了贝伦斯-费歇尔问题。许宝騄用一个一般的形式对这些问题进行了一揽子讨论,他创造性地引进统计量[2]
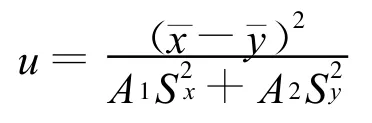
其中 A1>0,A2>=为常数,来讨论以|u|>c为否定域的检验。
当A1=A2=N/[n1 n2(N-2)],N=n1+n2时,则可导出u1,即Student t的统计量。
当A1=1/[n1(n1-1)],A2=1/[n2(n2-1)]时,则可导出贝伦斯-费歇尔问题的统计量u2。
许宝騄通过把u的密度函数展开成幂级数,研究了否定域|u|>c的势函数对参数的依赖关系。其主要内容是计算上述U检验的功效函数,并研究该检验在多种情况下的表现。
这是一个精确的(不是渐进的)分析,当代统计学家谢非称之为“数学严密性的范本”。据许宝騄的研究成果给出的检验方法后被称为“许方法(Method)”。
2 贝伦斯-费歇尔问题的解法
2.1 基于奈曼(Neym an)置信推断理论的解法
由于贝伦斯-费歇尔问题在实用上的重要性及其在估计理论中的历史作用,许多学者也研究了这个问题,但迄今为止只在以下三种情况给出了Frequentist(频率)精确区间估计:①σ1=σ2=σ未知的情况;②σ1/σ2=a已知的情况;③n1=n2的情况。对于一般情况尚未找到Frequentist精确区间估计。
(1)韦尔奇(Welch)的解法
韦尔奇在1938年给出了贝伦斯-费歇尔问题的一个近似解法。
Welch&Aspin给出了δ的置信水平为γ的近似置信区间[3]为

(2)谢非(Scheffe)的解法
1944年,谢非给出了服从t分布且含有参数μ1-μ2的一个枢轴量,从而得到了的置信水平为1-α的区间估计,给出了贝伦斯-费歇尔问题的一个解法[4]。

则有

又有Cov(Zi,Zj)=δij(i,j=1,2,…,n1),于是Z1,Z2,…,Zn1为来自总体 Z ~ N(μ1-μ2,+n1/n2)的简单样本,这样把原来的问题转化为检验总体Z均值的问题了。
若考虑以区间的平均长度为标准,这个解法有足够高的精确性。但美中不足的是,所构造的枢轴量并不是样本X1,X2,…,Xn1和Y1,Y2,…,Yn2的对称函数。这样一来,改变样本X1,X2,…,Xn1与Y1,Y2,…,Yn2的前后次序,就得到了不同的区间估计,而由样本的独立同分布性,人们自然地希望:样本的次序应与问题的解无关。
2.2 基于费歇尔(Fisher)信念推断理论的解法
费歇尔对贝伦斯问题给出了信念推断的区间,在这个问题中,充分地显示出置信推断与信念推断的区别。
设函数模型[5]
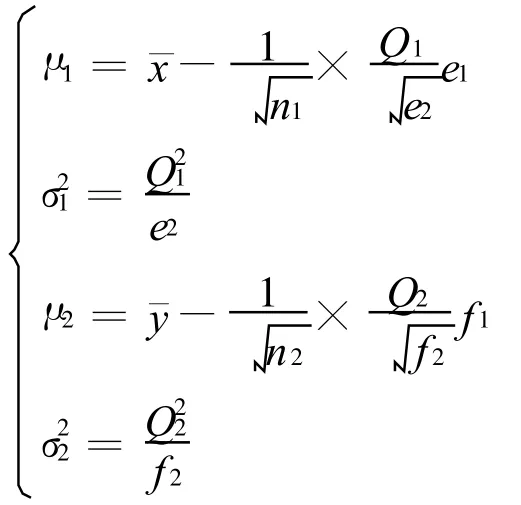
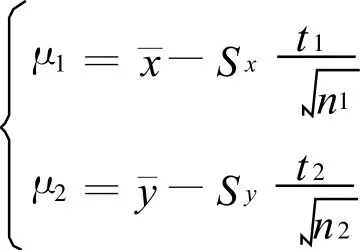
其中t1~t(n1-1),t2~t(n2-1),t1和t2相互独立,从而有

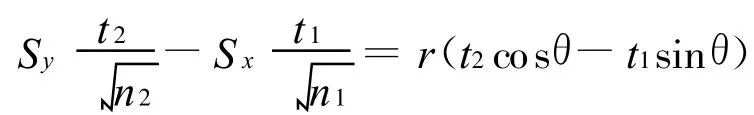
记W=t2 cosθ-t1 sinθ,显然W 的分布仅与 θ和t分布的自由度n1-1和n2-1有关。可以证明:W的分布关于原点对称。费歇尔等给出了δ的Fiducial信念水平为γ的Fiducial精确区间估计为(称为信念区间估计)
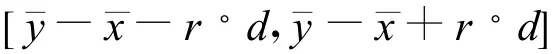
d值可在费歇尔和耶茨编的统计表中查出[6]。
此问题的解在信念分布的历史中有相当的意义。它对一个用频率学派方法难以处理的重要问题,给了一种明确的解法而不必涉及大样本,这说明它并非原有方法的改头换面的形式,而是能提供一些新东西。可以说,要不是贝伦斯-费歇尔问题,费歇尔的信念分布法可能早就被人遗忘了[2]。
费歇尔提出了信念推断方法,在他将此方法用于著名的贝伦斯-费歇尔问题之后,信念推断方法受到人们很大的关注,这说明信念推断方法是解决区间估计的一个有效的方法。另外,信念推断方法直观,它容易被实际工作者所接受。
但是,随着研究的深入,人们发现了信念推断方法的一些内在的问题。例如,在寻求信念分布的时候,利用不同的方法,推导出的信念分布有可能不一样。信念分布的这种不确定性是费歇尔的信念推断方法至今还没有被人们完全接受的原因之一。对于该信念推断,很多统计学家进行了批评。奈曼通过计算说明,费歇尔给出的信念水平为1-α的区间估计并不是置信水平为1-α的区间估计。所以有的时候信念水平为1-α的区间估计并不是置信水平为1-α的区间估计。
2.3 基于贝叶斯(Beyes)辩证推断理论的解法
两均值之差δ=μ1-μ2的精确区间估计或假设检验,H0:μ1=μ2,H1:μ1≠μ2,这里区分三种不同的情况,分别处理[7]。
现在考虑②、③两种情况。


于是记 x=(x1,…,xn1)′,y=(y1,…,yn2)′后 ,后验密度
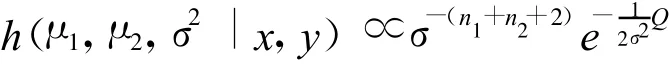
要求出 μ1-μ2的区间估计,只消求得 h(μ1,μ2|x,y),因此对 σ2从 0到 ∞积分,由 h(μ1,μ2,σ2|x,y)就得到
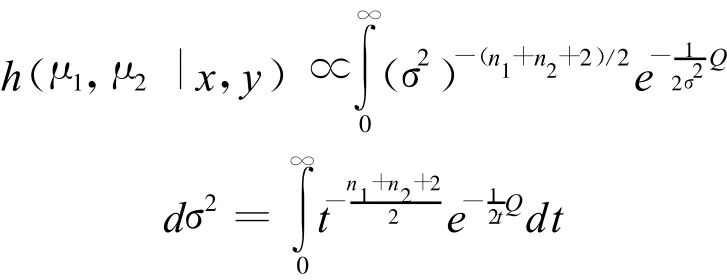
利用Γ函数的性质,就知道
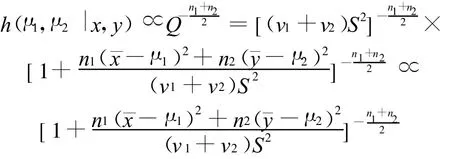
为了求得μ1-μ2的后验分布,考虑变换

此时相应的雅可比行列式是1,得到
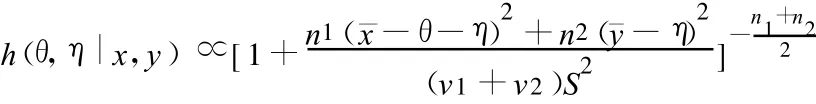
对η积分,就得
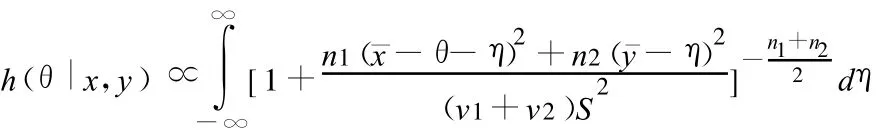
为了求出上式右端的积分,将被积函数的形式作一改写。令 z=η-,则
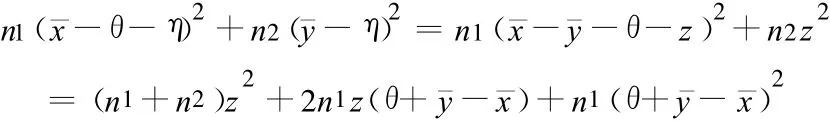


其中 v=v1+v2。取 t=后,从θ的后验密度,就得

这与经典方法的结果是完全一样的。
从贝叶斯方法看来,②与③的差别只是多了一个参数,在原则上是没有困难的。如果选先验分布时,考虑到两个总体是彼此无关的,应该相互独立,后验分布因此也相互独立,这样就可以两个总体各自处理,分别消除未知参数,的影响,于是就有后验密度
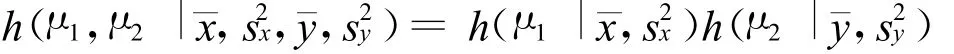
上式中的 h(μ1,)和 h(μ2,)可以用与 ②完全类似的方法求得。因此,用广义先验分布 π(μ1,)∝()-1,π(μ2,)∝()-1时,就有 h(μ1,)∝[1+,n1是来自 N(μ1,)样本的样本量,它正是自由度为n1-1的t分布。容易看出,对μ2也有类似的结果,即

n2是来自 N(μ2,)样本的样本量。令 t=
则有

于是可以算得密度为
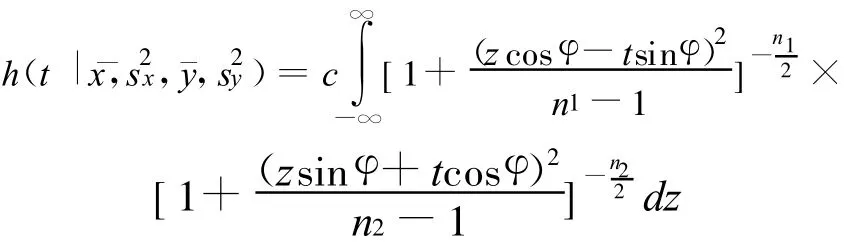
值得注意的是用费歇尔信念方法处理也得这一结果。
3 结语
关于费歇尔信念推断解法,置信推断理论的创立者奈曼在一项工作中进行了批评,奈曼主要提到两点:一是信念分布是含糊不清的,缺乏依据的,既然未对信念分布作出完全明确的定义而又借用通常概率论中的结果,提出这种批评是自然的;另一点是奈曼通过计算证明,这样定义的区间估计并不具备在他的意义下的置信系数1-α。奈曼就n1=12,n2=6和α=0.05的情况作了计算,说明由费歇尔方法作出的信念区间包含被估计的 μ1-μ2的概率,依赖于比值 ρ=σ1/σ2。当 ρ=0.1,1.0和10时,这概率分别为0.966,0.960和0.934。对后面这个批评,信念推断论者并不在意,因为他们并不认为,给区间估计以奈曼那种频率解释是不可或缺的,在他们看来,奈曼的计算结果的意义只在于证实了“信念系数”与“置信系数”确非一样的东西。事实上,更使人感兴趣的是:即使在这样较为复杂的场合,基于根本不同的出发点所建立的区间估计的“可靠度”有着很接近的值。
费歇尔信念推断理论是他的归纳推理体系一个主要组成部分,他是似然率、极大似然估计、充分性等归纳推理思想的继续[8]。信念概率及信念水平也是继似然率之后费歇尔信念的又一测度方法。但由于信念推断对于充分统计量、对于未知参数的统计量的精确抽样分布及其连续性等都有较严格的要求,因而在实际推断中不如置信推断来得方便。特别是对于两个参数或两个以上参数的较复杂推断问题,信念理论的局限性就更大了。不但所得结果与置信推断不同,而且对其解释也很困难。因而信念推断就被置信推断所取代,现代的教科书中也很少介绍信念推断方法了。尽管如此,费歇尔信念推断仍然闪烁着他归纳推理思想的杰出的火花。现在,也仍然有一些统计学家在努力完善费歇尔信念推断思想理论,并取得了一些进展。或许在将来某一天,费歇尔信念推断思想会重放光彩,重新引起人们的兴趣和重视。
1 Pao-Lu H su.Contributions to the Tw o-sample P roblem and the Theory of the “ Student's” t-test[J].Statist.Res.Mem.,1938(2):1-24.
2 陈希孺.数理统计学简史[M].湖南:湖南教育出版社,2002.
3 峁诗松,王静龙.数理统计[M].上海:华东师范大学出版社,1990.
4 陈希孺.数理统计学引论[M].北京:科学出版社,1981.
5 茆诗松,王静龙.高等数理统计[M].北京:高等教育出版社,德国:施普林格出版社,1998.
6 R.A.Fisher,F.Yates.Statistical Tables fo r Biological[M].Agricultural and Medical Research(5thed.),O liver&Boyd,Edinburgh,1957.
7 张尧庭,陈汉峰.贝叶斯统计推断[M].北京:科学出版社,1991.
8 袁卫.统计推断思想[M].北京:中国统计出版社,1990.
