正规族与正规函数的一个注记

戚建明

（山东大学 数学学院，山东 济南 250100）

正规族与正规函数的一个注记

戚建明

（山东大学 数学学院，山东 济南 250100）

设F为单位圆盘Δ上的一族全纯函数，a和b为2个有限的复数且有b≠a，如果对任意的z∈Δ且对每个f∈F，若f=α⇒f＇=α，且f=b⇒f＇=b，则存在一正整数M且对任意的f∈F，有

亚纯函数；正规族；Nevanlinna理论

1 引言及主要结果

设C为复平面，D为C上的一区域，F为一族定义在D上的亚纯函数，如果F在D上正规，那么对于F的任意一族子列{fn}⊂F，存在子序列{fnj}在D上局部一致收敛于一亚纯函数或者∞.[1]本文不失一般性，假定D=Δ={|z |＜1}.

设f和g为区域D上的亚纯函数，a和b为2个复数，如果f(z)=a则g(z)=b，我们记

如果f (z)=a⇔g(z)=a ，则称f和g分担a在D上．最近，很多学者[2-5]研究了亚纯函数分担值的问题.

f为C上的亚纯函数，如果存在一正数M，且满足

则f被称为C-正规函数[6]601.

f为Δ上的亚纯函数，如果存在一正数M，且满足

则f被称为Δ-正规函数[6]601.

Schwick[7]研究了正规族与分担值的问题，并证明了定理A.

定理A 设F为区域D上的一族亚纯函数，并且a,b,c为3个不同的复数，如果对每个f∈F，f和f＇分担a,b,c在D上，则F在D上正规.

定理A经Pang等[8]改进得到定理B.

定理B 设F为区域D上的一族亚纯函数，并且设a,b为2个不同的复数. 如果对每个f∈F，f和f＇分担a,b在D上，则F在D上正规．

2000年，Pang[6]研究了正规族与正规函数的关系，并证明了定理C.

定理C 设F为区域D上的一族亚纯函数，并且a,b,c为3个不同的复数，如果对每个f∈F，f和f＇分担a,b,c在D上，则存在一正整数M=M(a,b,c)并且对任意f∈F，有（1-|z|2）f#(z )=

注记1 定理C表明如果亚纯函数族F满足定理C的条件，则f∈F在D上是一正规函数.

显然，定理C对于分担3个不同的有限复数是成立的；那么，定理C是否对分担2个不同的复数成立呢？最近，Lü等[9]证明了下面的结果.

定理D 设F为区域D上的一族亚纯函数，设a和b为2个有限的复数且b≠a，若对于每一个f∈F 且z∈D，f=a ⇒f＇=a，并且f=b⇒f＇=b ，则F在D上正规.

注记2 对于2个不同的有限复数，定理D减弱了全纯函数分担值的条件，改进了定理B．

定理D能否像定理C那样改进是本文研究的问题. 本文中，我们主要研究了分担值的正规族与正规函数之间的关系，并得到了定理1.

定理1 设F为单位圆盘Δ上的一族全纯函数，a和b为2个有限的复数且b≠a，如果对于每一个f∈F且z∈D，f=a ⇒f＇=a，且f=b⇒f＇=b，则存在一正整数M并且对任何f∈F，有

注记3 例1说明对所有的f∈F，若满足定理1的条件，则其结果是正确的，因此定理1的情形可能发生.

注记4 定理1表明若任何一族全纯函数F满足定理1的条件，则f∈F在区域D上是一正规函数.

2 引理

引理1[10-11]设F为D上的一族亚纯函数，F在单位圆盘Δ上且对每个f∈F，其零点的重数至少为k．假定存在数A≤1，则f∈F且f=0时，有. 如果F在Δ上不正规，则当0≤α≤k，存在：l）一数r∈(0,1)；2）一复数列一函数列fn∈F ；4）一列正整数ρn→0+；且有局部一致地收敛于一非常数的亚纯函数g(ζ)在C上，并且g(ζ)的零点重数至少是k，g#(ζ)≤g#(0)=kA+1. 特别地，g的级至多是2.

3 定理1的证明

假定f不是单位圆盘Δ上的正规函数，则存在zn,zn＜1和函数fn∈F ，并且函数

满足

因此F={gn(z )}在Δ上不正规. 由引理1，且α=k=1和A=α+1，则存在：1）一数r∈(0,1)；2）一复数列一函数列fn∈F ；4）一列正整数ρn→0+；有：

在C上依球径一致收敛，并且

因此，由引理1，G(ξ)的级至多是1.

假定存在一点η0并且有G(η0)=0，则由Hurwitz定理，存在ηn,ηn→η0在n→∞时

于是，有

因此，G(ξ)的零点重数至少是2. 类似地，可证明G(ξ)-(b-a)的零点重数至少是2. 下面将证明G(ξ)≠(b-a). 假定η0是G(ξ)-(b-a)的一个零点且重数是m(m≥2)，则G(m)(η0)≠0；因此存在一正整数δ，且有

注意G(ξ)≡/b-a，由Rouche定理，则存在ηn,j(j=1,2,…,m)在上且有Gn(ηn,j)= b-a. 由式（1）并且注意f=b⇒f＇=b ，得到

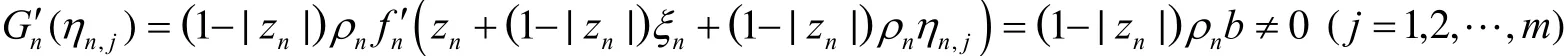
因此每一个ηn,j是Gn(ξ)-(b-a)的单零点，即ηn,j≠ηn,k(1≤j≠k≤m).

另一方面，

由Nevanlinna第一和第二基本定理，有

因此T(r,G)≤S(r,G)，这意味着G是一常数，矛盾，定理1获证.

注记5 从定理1，我们得到像定理D那样关于分担值的正规定则.

[1] HAYMAN W K. Meromorphic functions[M]. Oxford: Clarendon Press, 1964.

[2] LI Jiangtao, YI Hongxun. Normal families and uniqueness of entire functions and their derivatives[J]. Arch Math, 2006, 87: 52-59.

[3] LU Feng, XU Junfeng, YI Hongxun, Uniqueness theorem and normal family of entire functions and their derivatives[J]. Ann Polon Math, 2009,95: 67-75.

[4] MENG Chao. Uniqueness of meromorphic functions sharing one value[J]. Appl Math E-Notes, 2007, 7: 199-205.

[5] MENG Chao. Value sharing of entire functions[J]. Appl Math E-Notes, 2008, 8: 179-185.

[6] PANG Xuecheng, ZALCMAN L. Normality and shared values[J]. Ark Mat, 2000, 38: 171-182.

[7] PANG Xuecheng, ZALCMAN L. Normal families and shared values[J]. Bull London Math Soc, 2000, 32: 325-331.

[8] PANG Xuecheng. Normal family of meromorphic functions and normal function[J]. Chinese Ann Math Ser A, 2000, 21: 601-604.

[9] SCHWIEK W. Sharing values and normality[J]. Arch Math, 1992, 59: 50-54.

[10] XIAO Yonghou, LI Xiaoming. An entire function sharing one small entire function with its derivative[J]. Appl Math E-Notes, 2008, 8: 238-245.

[11] ZALCMAN L. Normal family’s new perspectives[J]. Bull Amer Math Soc, 1998, 35: 215-230.

A Note for the Normal Family and Normal Function

QI Jian-ming
(School of Mathematics, Shandong University, Jinan 250100, China)

LetFbe a family of holomorphic functions on the unit diskΔ, and letaandbbe two finite complex numbers such thatb≠a. If, for eachf∈Fandz∈Δ, f=a ⇒f＇=a , andf=b ⇒f＇=b , then there exists a positive numberMsuch that for any

meromorphic function; normal family; Nevanlinna theory

O174.52

A

1006-7302（2011）01-0006-04

2010-08-06

国家自然科学基金资助项目（10771121）；山东省自然科学基金资助项目（Z2008A01）；高等学校博士点专项基金资助项目（200604220409）

戚建明（1981—），男，江苏阜宁人，博士研究生，主要从事复分析理论与应用研究.