航空磁探仪目标运动分析仿真研究

李居伟，徐以成，孙明太

（海军航空工程学院青岛分院，山东 青岛 266041）

磁异常探测仪(Magnetic Anomaly Detection，简称磁探仪）是航空反潜飞机的主要搜潜装备之一，一般用于在发起攻击前对水下目标进行跟踪和定位。许多文献都指出，作为一种被动探测手段，与其他探潜设备相比，磁探仪具有很多优势。如可以连续搜索、分类能力好、定位精度高等[1-3]。文献[4]和文献[5]从信号处理角度研究了磁探仪的定位模型。结果表明，不同的定位模型主要影响磁探仪的探测距离和探测虚警率。这些文献主要涉及到磁探仪的作用范围、目标识别和搜索效率等问题。而对水下机动目标而言，攻击前的“目标定位”不仅包括获取目标的位置信息，还要解算目标航速和航向等信息，并给出定位误差，借以控制攻潜武器的投放。目前尚未发现有关这方面的文献资料。

一般情况下，磁探仪无法确定目标的精确位置，只能通过与目标的连续接触，估计目标航速和航向等运动要素。这正是本文的主要研究内容。对磁探仪而言，确定目标运动情况最简单直观的方法是：将发现磁异常信号时反潜机的位置标定为“目标位置”，将多个这样的“目标位置”点连线或拟合为一条直线，视其为目标运动轨迹，求解运动要素。这样处理有一定的合理性，但无法确定目标航速、航向的估计误差。然而，对目标运动参数误差的估计，在攻潜作战中非常必要。一是可以借以确定攻潜武器的使用方式（包括武器类型、投放参数等）；二是可以借以预测武器攻潜的效果，进而为下一步行动提供决策依据；三是可以借以确定磁探仪的使用方法（如确定其探测范围、使用高度等），以便更为精确地跟踪目标，估计其运动状态。

鉴于此，本文采用蒙特卡洛仿真方法，研究了航空磁探仪对目标运动要素估计误差的分布规律，给出了运动要素误差的简化算法，并分析影响因素。

1 基本假设

磁探仪作为一种被动的探测器材，在反潜飞机上使用时，一般不易被水下潜艇发觉。在反潜作战中，磁探仪往往使用在潜艇活动受限的海域，如狭窄海峡、水道等，或其他探测器材已发现潜艇并测得潜艇位置误差满足一定条件时[6]。因此，在仿真计算中，假设潜艇目标作深度不变的匀速直线运动。

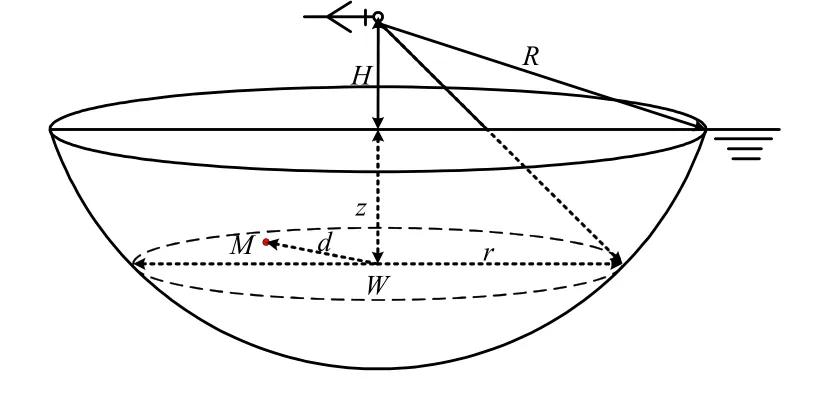
图1 目标分布范围示意图

磁探仪探测范围为图1所示的球冠形状，一般情况下，磁探仪只能判断目标存在于该区域内。因此，假设潜艇目标在该球冠内均匀分布。

计算中，假设水下潜艇为一点状目标。因为当磁探仪到目标的距离大于3倍的目标尺寸时，可以将其磁特性等效为一个磁偶极子的磁场[7]。即使采用潜艇磁场的精确模型（如旋转椭球体与偶极子阵列混合模型等），其磁场效果也同单磁偶极子类似。

不考虑探测范围接触海底的情况。作战中，往往根据海域情况和潜艇特性选择飞机的飞行高度，尽量使探测范围涵盖潜艇所有活动深度。在较浅海域，可以通过增加飞行高度提高定位精度；也可以通过降低飞行高度扩大搜索范围。在最后攻击阶段，一般以提高定位精度为准。

2 计算方法

2.1 随机目标位置的选取

如图1所示，设磁探仪的最大探测距离为R，飞机飞行高度为H，探测范围在深度z处的宽度W为

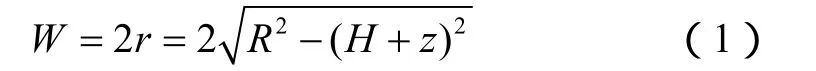
设随机选取的目标位置为 M ( x, y, z)，x, y为水平面坐标，z为目标深度，都服从相互独立的均匀分布。产生方法如图2所示。

图2 目标随机位置产生流程

2.2 目标可能轨迹的确定

通常实施磁探仪探测战术时，必须做好投放武器的准备。一般保持3～4次连续接触，解算出目标运动轨迹，便可投放攻潜武器。解算目标运动轨迹的主要任务是确定目标航速V和航向β。如图3所示。

图3 目标运动轨迹平面示意图

图3中各圆的圆心为磁探仪发现磁异常信号的位置（以下称为探测点），平面坐标分别为o2( xo2, yo2)、o3( xo3,yo3),…，对应的接触时刻为t1, t2, t3,…。每个圆代表了一个形如图1的目标分布范围，记为

假设目标作等深度匀速直线运动，目标可能的运动轨迹应当穿过所有的目标分布范围。则目标可能的运动轨迹便可通过如下步骤获取：

Step1：在t1时刻的目标分布范围C1内，按均匀分布的规律随机选取目标可能位置 M1(x1, y1, z1)。选取方法见2.1。

Step2：采用与Step1相同的方法，按均匀分布的规律，在目标分布范围C2内随机选取t2时刻的可能目标位置 M2( x2, y2, z2)。其中，目标深度保持不变：z1＝z2。

Step3：M1和M2两点可以确定一条直线，以此计算目标可能航向β；根据两点间隔和探测时刻计算目标可能航速V。

令 Δx ＝ x2-x1， Δ y ＝ y2- y1，则有

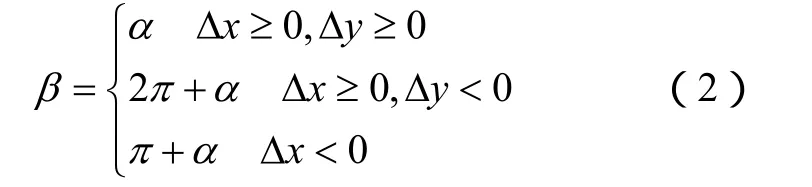
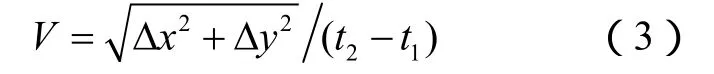
Step4：假设目标按照Step3中计算的目标航速和航向运动，则t3时刻目标的位置 M3( x3, y3, z3)可以表示为

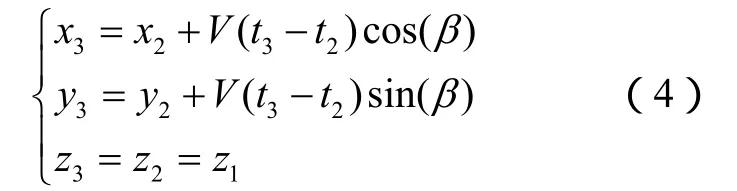
Step5：判断Step4中目标位置 M3(x3, y3,z3)是否在目标分布范围C3内。判断标准为：若d≤r，转入Setp6；若d＞r，则 Step3中计算的目标航速和航向不合理，转入Setp1重新计算。d、r如图1所示，分别为

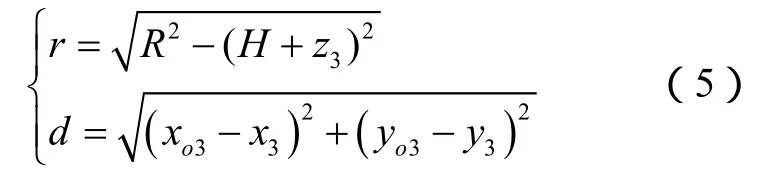
Setp6：记录Step3中航速、航向的计算结果，作为目标可能的一个运动轨迹。

3 算例分析

假设磁探仪与目标接触3次，各探测点坐标o1、o2、o3分别为(0,0)、(750,600)、(1580,1220)(单位：m)；接触时刻t1、t2、t3为0、190s、200s；磁探仪探测距离R为400m，飞机飞行高度H为100m。

3.1 目标航速、航向误差规律和确定方法

首先，采用最简单直观的最小二乘法，将探测点o1、o2、o3拟合为一条直线：

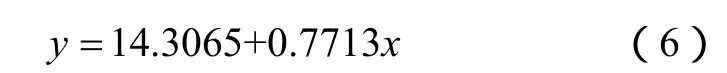
如果以此作为目标运动轨迹，则可以得到目标航速和航向的最小二乘拟合值，见表1中的最小二乘合成值。这种方法无法给出航速和航向的估计误差。

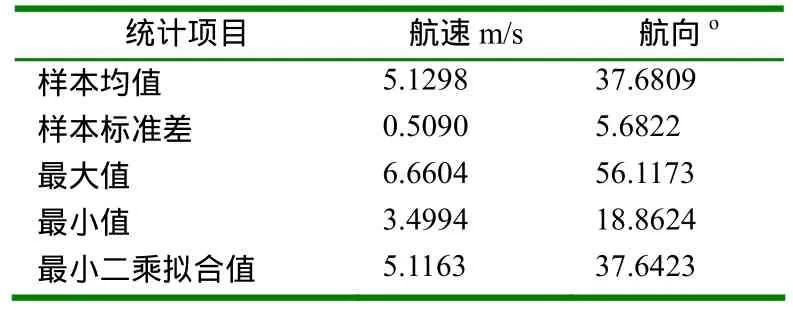
表1 目标航速、航向统计数据

在此基础上，根据2.2中的计算步骤，采用蒙特卡洛仿真方法，进行10000次仿真，得到2408个可能的目标运动轨迹。将其视为统计样本，得到一系列统计数据见表 1。同时，用柱状图的形式描述所有可能航速、航向的分布密度情况，如图4和图5所示。

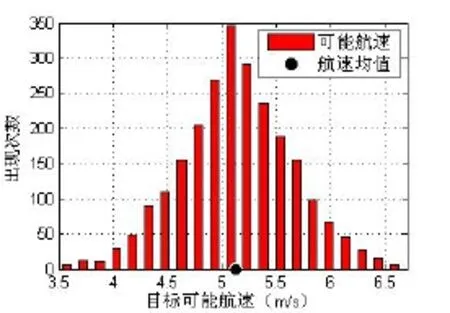
图4 目标可能航速分布情况

图5 目标可能航向分布情况

分析如下：

1）最小二乘法拟合得到的航速、航向与蒙特卡洛方法仿真统计得到的航速、航向样本均值十分吻合。

2）图4、图5中显示，目标航速、航向分布密度基本近似为以样本均值为中心的正态分布；并且基本符合正态分布的3σ准则。即将航速、航向的样本标准差作为均方差 σV,σβ的估计值，满足如下关系：

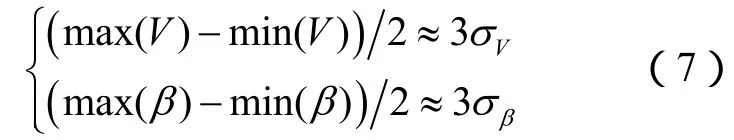
3）为进一步验证目标航速、航向样本数据的正态性，采用单样本 K-S（Kolmogorov-Smirnov）正态性检验方法，对2408个可能的航速、航向值进行检验。结果表明：在0.05的显著性水平下，两者均服从正态分布，即

4）通过不同初始数据的多次仿真，都得到了类似的结果，因此认为上述规律具有普遍性。

3.2 目标运动要素误差的简化算法

上述蒙特卡洛法仿真算例的分析表明：目标的航速、航向可以采用正态分布的形式近似表达。并且，均值可以采用最小二乘法，将探测点拟合为一条直线得到。均方差可以由所有可能航速、航向的极值确定。而根据磁探仪多次接触目标得到的多个目标分布范围的几何关系，目标可能航速、航向的极值较容易求得。

这样结合式（6）和式（7），便可得到目标运动要素误差的简单计算方法，从而不需要进行大量的统计计算，提高了算法的实时性。基于此，在分析磁探仪的探测精度、估计攻潜武器使用效果时，便可以使用上述算法的计算结果。

3.3 误差影响因素分析

设定探测点的间隔时间一定，间隔距离变化时，记录每次仿真的目标航速均值，以及所有可能航向、航速的均方根误差（RMSE:root-mean-square-error），得到图 6和图7。其中，横坐标“目标航速均值”与探测点间隔一一对应。

图6 探测点间隔对航向误差的影响

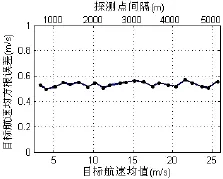
图7 探测点间隔对航速误差的影响

探测点的间隔对使用磁探仪测定目标运动要素的精度影响很大，特别是目标航向，见图 6。结果表明，在探测点间隔时间一定的情况下，目标航速越大，则探测点间隔距离越大，此时测定航向误差越小，而对测定航速的影响不大，如图7所示。由此分析如下：

1）对速度较高的目标，由于探测点间隔较大，测定目标航向的估计误差较小，磁探仪的探测效果较好；

2）作战中，当发现目标速度较低时，可以通过较多次的接触，从中选取间隔距离较大的探测点，进行目标运动要素解算，以提高解算精度。

4 结束语

航空磁探仪作为一种重要的搜潜设备，确定其目标运动要素解算精度对于攻潜武器的使用，以及作战效果的评估至关重要。本文分析了使用磁探仪估计水下潜艇目标航速、航向误差一般服从正态分布的规律，给出了简化算法；探讨了探测点间隔对误差的影响。研究结果可以为航空磁探仪的使用、攻潜武器的确定和攻潜效果评估提供参考。

[1]梁志诚.现代反潜武备[M].北京：海潮出版社，2003.

[2]孙明太.航空反潜概论[M].北京：国防工业出版社，1998.

[3]E. Paperno, I. Sasada, E. Leonovich. A New Method for Magnetic Positioning and Orientation Tracking[J].IEEE Trans. Magn., 2001, 3(7): 1938-1940.

[4]R. N.Forrest.Notes on Search, Detection and Localization Modeling[R]. Naval Postgraduate School Report NPS71-87-001, April 1987.

[5]R. N. Forrest. Magnetic Anomaly Detection Models[R].Naval Postgraduate School Report NPS55-77-19,April ,1988.

[6]海军装备论证中心.国外反潜战[M].北京：海军出版社，1987：356-360.

[7]J. A. Baldoni, B. B. Yellen. Magnetic tracking system:Monitoring heart value prostheses[J]. IEEE Trans. Magn.,2007, 4(3): 2430-243.