几种野值剔除准则在目标预测中的应用研究

卢元磊，何佳洲，安 瑾，苗高洁

（江苏自动化研究所，江苏 连云港 222006）

在目标预测中，由于目标测量数据采集过程受传感器、转换器以及无线电传输过程中的干扰，使得接收数据中经常会产生异常跳变点，这种偏离被测信号变化规律的数据点被称为野值[1[。如果在数据预处理阶段不将野值剔除，那么这些野值将会严重影响目标预测的精度，甚至会导致目标预测的发散。因此，如何剔除野值成为目标预测中的首要问题。本文分析了目标预测中的野值剔除问题，介绍了误差理论中几种常用的野值剔除准则，并通过仿真分析了它们对野值的剔除能力及对目标预测精度的影响。

1 目标预测中的野值剔除问题分析

1.1 问题描述

野值的定义有很多种，一种比较公认的且与目标预测中的野值剔除比较贴切的定义是 Barnett 和Lewis在1984年给出的定义：野值就是一个观测数据集中与其他数据表现不一致的一个或多个观测点组成的子集[2]。

目标预测中的野值剔除和常规误差理论中的野值剔除是有区别的。在常规的误差理论中，野值剔除是进行重复多次测量，然后对观测数据的事后处理。在目标预测中，目标状态不断变化，每个状态都是单次测量，而且要求数据的处理是实时的、在线的，随着目标的运动，测量环境和精度也是发生变化的。因此，这对两种情况的处理方法也是有区别的。在常规的误差理论中通常取多次测量的均值来替代目标的真实状态，且大多数情况下是可行的。但在目标预测中，我们必须通过一定的手段对目标当前状态进行估计来求取观测误差。

除了目标状态的估计会影响目标预测中的野值剔除性能，不同的野值剔除准则也会影响野值剔除的性能。例如，在某些情况下，即使一些比较公认的野值判别准则有时也会把一些非野值点误判为野值，相反在另外一些情况下这些准则对一些野值点反而不能有效地剔除[3[。比较实用的准则是根据具体的情况，选择合适的判别准则使得在野值的剔除率和误剔除率之间取得一个较好的平衡。

目标观测中野值分为孤立型野值和斑点型野值。孤立型野值是指野值点不是连续出现的，斑点型野值点是指野值成片出现的野值。本文主要针对孤立型的野值点。

1.2 传统3σ准则分析

目标预测中最常用也是最简单的判别野值的准则是莱特准则，也称3σ准则。

对于某一量测列，若量测只含有随机误差，则根随机误差的正态分布规律，其残余误差落在±3σ以外的概率约为 0.3%，若发现有大于3σ得残余误差的量测值，则可以认为该点是一个野值点，应予剔除。但存在如下一些问题：

1）3σ准则假定所有的观测样本的服从于同一个正态分布，在测量次数充分大的情况下，通过大量的样本所求的样本标准差s近似等于测量误差的标准差σ。但是，在目标跟踪中，存在两个主要的因素导致实际情况不能满足该前提条件。

在目标预测中，由于目标的运动可能导致观测距离和观测环境会发生改变，观测的精度就会发生变化。所以，传感器的观测误差的标准差可能是变化的，在不同时间段可能服从不同的分布。另一个原因是，目标当前时刻的状态估计是不准确的。例如，在相同的观测精度下，在目标匀速直线运动阶段，状态估计相对更准确，这一过程统计的标准差就会相对小。而目标发生机动时，状态估计可能会以某种规律存在一个规律性偏差，那么这一阶段统计的样本标准差可能会比较大。因此，3σ准则在目标跟踪中的应用只是一个近似的准则。

2）标准的3σ准则判别公式为

目前在目标跟踪中3σ准则的应用形式为

2 误差理论中几种常用的野值剔除准则

2.1 奈尔准则

式中，σ为已知的观测误差总体标准差。

奈尔推导证明出统计量r的分布函数为

奈尔检验的临界值见文献[4]。选定显著性水平α，由n查表确定临界值R(α,n)，可以得到

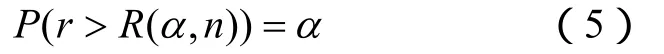
因此有如下的判别准则：若统计量

则认为对应的观测值xi为野值，应予剔除；否则为正常值，保留在观测数据中。

2.2 格拉布斯准则

由于目标的运动是连续的，因此在一段时间tm内，观测环境可以近似认为是不变的。雷达的观测精度也可近似认为是恒定的。在时间tm内，雷达的观测误差可认为服从同一个概率分布。如果用tm时间内的样本来统计样本标准差，则能够更真实地反映当前时刻的观测误差标准差。

而在小样本情况下，观测误差已经不再服从正态分布。下面格拉布斯[5]推导出了在小样本条件下，观测误差的概率分布情况。

式中，

格拉布斯推导出了统计量g的理论分布[1]。

格拉布斯的临界表可参见文献[4]。选定显著性水平α，由样本数n查表确定临界值G(α,n)，可以得到

格拉布斯判别准则如下：若统计量

则认为对应的观测值xi为野值，应予剔除；否则为正常值，保留在观测数据中。

统计分析表明：对于测量样本在n=30～50时，用格拉布斯准则效果较好，可靠性较高[6]。样本标准差s只用最近n个滤波值进行统计，然后根据样本数和显著性水平α确定判别门限。

在实际工程应用中，由于滤波器的性能和雷达的探测精度等因素的不同，统计的样本数n和显著性水平α可以根据实际情况而确定。

2.3 狄克逊准则

狄克逊准则[8]是直接根据测得值的顺序统计量，采用极差比的方法里判别可疑数据是否为异常值的，避免了数据列的算术平均值、残余误差和标准差反复计算。在本文中，我们选择观测样本数n=20，则有观测误差序列：

首先对观测误差序列进行从小到大排序，形成新的观测误差序列：按照判断待检验观测误差是否是最大值或最小值。

如果待检验的观测误差是最大值，则构造统计量：

如果待检验的观测误差是最小值，则构造统计量

狄克逊推导出了这些统计量的分布函数[10]，并给出了计算的临界表[4]。查表得到狄克逊准则的临界值D(α,n)，则

狄克逊准则的判别公式如下：若统计量

则认为对应的观测值xi为野值，应予剔除；否则为正常值，保留在观测数据中。

在标准差已知时，通常采用奈尔准则；标准差未知时，采用3σ准则、格拉布斯准则、狄克逊准则和精细准则；格拉布斯布斯准在在测量样本n=30～50时效果较好，可靠性较高；若需要迅速判别野值，可以选用狄克逊准则[4[。

3 仿真验证

3.1 仿真设置

针对单部雷达观测空中目标的情况进行目标航迹预测，雷达的探测精度设置为80m和0.5deg。剧情一：目标在距离雷达50km处以300m/s的速度做运动半径为10km圆弧运动；剧情二：目标先匀速直线运动，在距离观测雷达10km处开始比例导引运动。

每条观测航迹中随机地加入5个野值点。假设观测误差服从正态分布，根据正态分布的统计特性可知，观测误差大于 3倍标准差的观测值出现的概率只有0.27%。从统计学的角度而言，这是一个小概率事件，基本上不会发生，一旦发生可认为该观测值为野值。本文随机的选择五个真实状态，在其上加或减 3～10倍的标准差作为观测值，则这5个观测点即是观测数据中的野值点。

在以上的剧情条件下，本文选择基于当前统计模型的标准卡尔曼滤波器估计目标当前状态，机动频率设为1/60。目标预测的方法采用常用的二次多项式拟合外推预测，预测时间为1s。

野值剔除性能主要通过以下两个指标验证：一是野值的漏剔除率，如果观测数据中含有未被剔除的野值，会大大影响目标预测的精度，从图1（a）中可以看出，因此野值的漏剔除现象会影响目标预测的稳健性；二是野值的误剔除率。有些野值剔除准则会将一些随机误差当成野值剔除，这就造成观测数据中的有效信息损失。在目标状态估计不精确的情况下，野值的误剔除很容易将目标的机动误判为野值，这将对目标预测精度造成很大的损失。因此这两个指标能够较好的反应准则的野值剔除能力。

目标预测精度的指标为整条航路预测误差的均值。

3.2 仿真结果及分析

1）目标圆弧运动，单次运行结果

从图1（a）中看出在野值未剔除的情况下，目标的预测航迹受到了野值的严重影响；图1（b）中观测数据经过格拉布斯准则将野值剔除，因此预测航迹相对更平滑更接近真实状态，预测的精度远远大于野值未剔除的情况。

2）目标比例导引运动，单次运行结果

目标在比例导引运动时，野值如果不进行剔除处理同样会大大降低目标预测的精度，甚至导致预测值是无效的，从图2（a）中可以看出。图2（b）中野值剔除后，由于目标距离近，观测精度高，因此预测的精度很高。

图1（a）野值未剔除的预测航迹

图2（a）野值未剔除的预测航迹

3）野值剔除性能分析

设定野值剔除的判别显著性水平α为 1%，仿真结果如表1所示。

表1 目标圆弧运动，运行200次统计结果

从表1可以看出，目标做圆弧运动时传统的3σ准则虽然能将野值剔除但野值的误剔除率较高；狄克逊准则野值的误剔除率较低但存在野值漏剔除的现象；奈尔准则性能最好，但要求观测误差的分布精确已知且要求目标状态估计准确；格拉布斯准则能能够将野值剔除且误剔除率保持在一个较低的水平。

表2 目标比例导引运动，运行200次统计结果

目标在做比例导引运动时观测距离较近，因此观测精度较高，目标状态估计的就相对精确，普遍提高了野值的剔除的性能。从表2看出，3σ准则出现了野值的漏剔除现象。这是因为随着目标的靠近，观测误差的标准差逐渐减小，而3σ准则统计的误差标准差大于实际的标准差，因此误剔除率较低，同时出现了漏剔除的现象。狄克逊准则仍然存在漏剔除的现象。格拉布斯准则没有出现野值漏剔除的现象，误剔除率保持在一个较低的水平，具有较好的野值剔除性能。

4）目标预测精度分析

表3 目标预测误差的统计结果

从表3中首先可以看出一个明显的现象：观测数据进行野值剔除处理后大大提高了目标预测的精度。各个野值剔除准则处理后目标预测的精度也是不同的，3σ准则野值的误剔除率较高，有时会出现漏剔除现象，目标预测误差大于格拉布斯准则；奈尔准则野值剔除的性能最好因此目标预测的精度最高，但要求观测误差分布已知且目标状态估计要精确，实际中很难达到这样的条件；格拉布斯准则应用条件比较宽松便于实际应用，且具有较好的野值剔除性能，相对于3σ准则和狄克逊准则能取得更好的预测精度。因此在目标预测的预处理过程中，采用格拉布斯准则是比较合理的选择。

4 结束语

野值剔除的性能会影响目标预测的精度。本文首先对目标预测中野值剔除问题和传统的的剔除方法进行了分析，引入了误差理论中几种常用的野值剔除准则，并将其应用于目标预测中的预处理。通过仿真算例表明，利用野值剔除准则将观测数据中的野值剔除后能大大提高目标预测的精度。不同的野值剔除准则对目标预测精度的影响也是不同的：传统的3σ准则野值误剔除率较高且某些情况下存在漏剔除的情况，目标预测的精度要低于其他几种准则；在观测误差标准差能够获知且目标状态估计准确的情况下，奈尔准则能够获得较好的野值剔除效果和最高的目标预测精度，但这些前提条件在实际中很难满足；格拉布斯准则没有出现野值漏剔除的现象且误剔除率保持一个较低的水平，野值剔除的综合性能较好，目标预测的精度高于3σ准则和狄克逊准则；狄克逊准则存在野值漏剔除的现象，不能保证预测的稳健性，因此统计的预测精度较差；综合比较，格拉布斯准则由于具有较好的野值剔除性能，是目标预测预处理中一种比较理想的野值剔除准则。

[1]费业泰.误差理论与数据处理[M].合肥:合肥工业大学出版社,2005.

[2]Barnett,V..T. Lewis. Outliers in Statistical Data[M]. 2nded. New York: John Wiley & Sons. A well-Written Comprehensive Text on outliers,1984.

[3]Boris Iglewicz, David C. Hoaglin, How to Detect and Handle Outliers[M]. ASQ (American Society for Quality Statistics Division),1993.

[4]王中宇,刘智敏,夏新涛,等.测量误差与不确定度评定[M].北京:科学出版社,2008.

[5]Grubbs F E. Sample Criteria Testing Outlying Observations[J]. The Annals of Mathematical Statistics,1951, 22(1):68-78.

[6]沙定国.误差理论与数据处理[M].北京:北京理工大学出版社,1993.

[7]金学军.基于最小二乘拟合的外弹道测量数据野值剔除方法[J].四川兵工学报,2011,32(1).

[8]刘智敏.计量常用数学基础[M].北京:中国计量出版社,1997.

[9]BIPM, IEC, IFCC, et al. Guide to the Expression of Uncertainty in Measurement[D].Switzerland:ISO,1995.

[10]刘智敏,陈坤尧,翁怀真,等.测量不确定度手册[M].北京:中国计量出版社,1997.