谈如何指导学生在高考中轻松解题
2011-07-14范建华
范建华
(栟茶高级中学 江苏 如东 226406)
高三学生对于高考是“既期待又害怕”.期待能在高考中斩获优异成绩,同时又害怕在高考中出师不利.笔者认为考生如果要想在高考中发挥出自己的最高水平,解题的技巧至关重要.笔者在指导毕业班学生时经常打的一个比方是,题目就像一团毛线,不能把它拿在手里不分青红皂白地就扯,而应该根据毛线团的情况去理.同样,怎么才能很好地将题目的思路理顺,快速且顺利地解题呢?笔者接下来结合部分高考题和模拟题,介绍如何指导学生从四个典型思路着手轻松解题.
1 适时调整解题思路
高考中有些题目乍一看题型没见过或解题过程很繁琐,其实不然.当你发现用最初想到的解题思路解题困难重重时,这就需要冷静分析题目所要考查的知识点,适时调整解题思路,从比较熟悉的知识或非常拿手的方法开始着手分析,或许会有意想不到的收获.
【例1】(2010年高考江苏卷第3题)如图1所示,置于水平地面的三脚架上固定着一质量为m的照相机,三脚架的三根轻质支架等长,与竖直方向均成30°角,则每根支架中承受的压力大小为
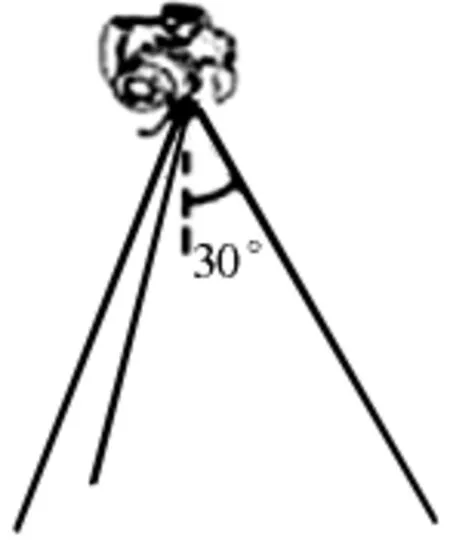
图1

解析:这道高考题要求解的是每根支架中承受的压力大小,其实就是求解每根支架对照相机的支持力.这个考生们基本都能想到,而且大部分考生也都知道三根支架给照相机的支持力大小相等,且三个力的合力与照相机的重力平衡,即三个力的合力大小等于mg.但这道题目解题的难点也随之出现了,不少学生就在思考“这三个支持力不在一个平面内,该怎样合成呢?平时只学过同一平面内的力的合成啊!”.这时就需要学生调整思路.空间里的三个力直接合成肯定是有困难,如果先分别将三个力分解到水平和竖直方向,题目就能迎刃而解.分解后结合空间立体图形分析会得到支持力在水平方向三个分力的合力为零;竖直方向三个分力的合力大小等于重力.可以算出支持力的大小为
2 警惕凭“感觉”解题
有些题目看上去很“眼熟”,但仔细推敲后却发现与之前所熟悉的题目有很大的差别.
【例2】(1)如图2所示,光滑水平面上有四个质量均为1kg的物块,施加大小F=4N的水平推力,求3,4两个物块间的弹力大小.
(2)如图2所示,动摩擦因数μ=0.2的水平面上有四个质量均为1kg的物块,施加大小F=4N的水平推力,求3,4两个物块间的弹力大小.

图2
解析:这里的第(1)题比较简单,通过先整体再对物块4隔离可以得出3,4两物块间的弹力为1N.
第(2)题乍一看与第(1)题也差不多,也是通过“先整体再隔离”求解.
不少同学的分析过程如下,对于整体,地面提供的最大静摩擦力为8N,水平推力小于最大静摩擦力,则物块保持静止.物块4在整体的最前面,质量为整体的则物块3给物块4的作用力也为推力大小为1N.而且这些同学还判断了1N小于地面给物块4的最大静摩擦力2N,所以物块4是保持静止的.
这种错解显然是受第(1)题的解题思路的影响而凭感觉猜出来的.这道题目需要学生知道弹力的一个产生条件是“发生弹性形变”.在这里物块3和物块4之间怎样才能发生形变呢?很明显物块3要向前移动挤压后才能发生形变,而要使得物块1,2,3这个整体向前移动,推力F必须大于这三个物块的最大静摩擦力,计算发现推力4N小于这三个物块的最大静摩擦6N,所以物块3与物块4之间弹力为零.
3 探索“新情境”题目的本质
高考的题目越来越活,物理情境越来越新.有些题目考生看到后的第一感觉用一个字“蒙”来形容都不为过.当在遇到新的物理情境时,应从基本的解题思路着手分析.比如进行受力和运动情况的分析,或许能发现题目和之前见过的某个题目的情境类似.
【例3】(2010年高考江苏卷第1题)如图3所示,一块橡皮用细线悬挂于O点,用铅笔靠着线的左侧水平向右匀速移动,运动中始终保持悬线竖直,则橡皮运动的速度
A.大小和方向均不变
B.大小不变,方向改变
C.大小改变,方向不变
D.大小和方向均改变
解析:这道题考查运动的合成,情境较新.在仔细分析后会发现由于悬线竖直,则橡皮和铅笔在水平方向的运动状态相同,所以橡皮沿水平方向做匀速直线运动.另外,铅笔两侧细线的总长度保持不变,铅笔向右匀速运动使得铅笔与橡皮间的悬线均匀变短,所以橡皮竖直向上做匀速直线运动.综合橡皮在水平方向做匀速直线运动,在竖直方向做匀速直线运动,则橡皮的合运动是匀速直线运动,速度的大小和方向均不变.
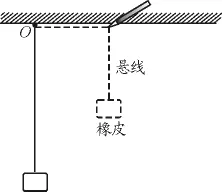
图3
4 列“主干表达式”轻松解题
学生通常解计算题时就像处理毛线团一样,拿在手上无处下手,胡乱扯一通,绝大多数情况下是扯到最后依然乱糟糟.
其实不管题目难还是易都会有一个着手点,这个着手点就是解题的突破口.由这个突破口列出“主干表达式”,然后再列出“分支表达式”对“主干表达式”中的一些未知量进行求解、补充.
如何找到解题的突破口,从而列出“主干表达式”?笔者总结出了如下的寻找突破口列“主干表达式”的方法.
(1)由题目最后的问题着手.
(2)由题干中熟悉的知识点或常见模型着手.
【例4】(2011年江苏苏北四市调研第14题)如图4所示,电阻不计且足够长的U型金属框架放置在绝缘水平面上,框架与水平面间的动摩擦因数μ=0.2,框架的宽度l=0.4m、质量m1=0.2kg.质量m2=0.1kg、电阻R=0.4Ω的导体棒ab垂直放在框架上,整个装置处于竖直向上的匀强磁场中,磁感应强度大小B=0.5T.对棒施加如图4所示的水平恒力F,棒从静止开始无摩擦地运动,当棒的运动速度达到某值时,框架开始运动.棒与框架接触良好,设框架与水平面间最大静摩擦力与滑动摩擦力相等,取g=10m/s2.求:
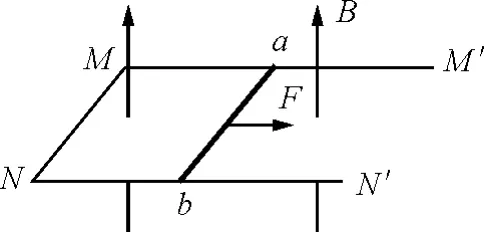
图4
(1)框架刚开始运动时棒的速度v;
(2)欲使框架运动,所施加水平恒力F的最小值;
(3)若施加于棒的水平恒力F为3N,棒从静止开始运动0.7m时框架开始运动,求此过程中回路中产生的热量Q.
解析:以这道题目的第(1)问为例,需要求解框架刚开始运动时棒的速度v.通过分析可知框架刚开始运动时的状态是平衡状态,MN边所受安培力的大小等于其所受的最大静摩擦力.故可根据平衡条件列出主干表达式
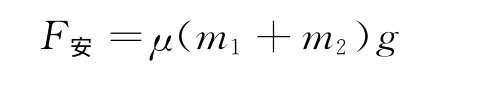
然后再列出求解主干表达式中F安的分支表达式

可解得v=6m/s.
这个题目的解决过程就没有直接为了求解速度v而一味地思考怎样直接求解这个速度v.而是从大家较熟悉的平衡条件入手,先列出主干表达式,再列出分支表达式作补充.最终所要求解的速度v就自然而然地解出来了.
题目学生解不出来不一定是所考查的相关知识不会,而可能是对于解题的思路、方法、技巧的缺失.对于学生的考前指导不能泛泛而谈,应该更有针对性地指导学生在遇到各类具体情况时该如何处理.只有这样的解题指导才是真正对学生有用的指导.
