基于能量原理的均质土坡临界坡高计算

蒋跃楠,吴继敏

(1.河海大学土木与交通学院,江苏南京 210098;2.宜兴技师学院,江苏 宜兴 214200)

刚体极限平衡法是常用的边坡稳定分析方法,虽然该方法无法考虑材料的应力-应变关系,不能给出相应的应力场和位移场,但是其概念清晰,计算简便,工程实践资料丰富.事实上,在实际工程中,人们关心的并不是边坡失稳的整个过程,而是开始滑动那一瞬间边坡的极限承载能力或者相应的临界坡高.极限分析法中的上限法恰好回避了工程中最不容易弄清的岩土应力-应变关系,从能量角度直接研究边坡的极限状态,因而是一种合理而且可行的方法.对于处于极限平衡状态的边坡(包括人工边坡、自然斜坡等),其坡度及岩土体的物理力学性质是确定的几何物理力学参数,依据能量原理推算的临界坡高,可用来评判边坡的稳定性[1].

根据已有的研究成果[2-3],无黏均质土坡破坏时的滑面近似平面,在剖面上呈一条直线,通常用直线滑裂面进行稳定性分析;黏性均质土坡,由于黏聚力的存在,破坏时滑动面是一个曲面,曲率半径上部小、中间大,在断面上与椭圆弧相似,通常用对数螺旋滑裂面进行稳定性分析.国外一些学者经过大量的计算发现,由于土的内摩擦角、土坡坡角、硬层的埋置深度等因素的相互影响,土坡破坏时,可能出现3种不同位置的滑动面:坡脚滑弧、坡面滑弧和中点滑弧,如果土的内摩擦角大于3°,一般产生坡脚滑弧[4].

本文应用外功率和内能耗散率相等的原理[5-6],针对黏聚力较小的黏性均质土坡有可能产生沿直线滑裂面滑动及沿对数螺旋滑裂面滑动的情况分别进行临界坡高的探讨,并结合实例分析土坡临界坡高的计算方法.

1 均质黏性土坡的临界坡高探讨

图1 直线滑裂面示意图Fig.1 Sketch of linear slip surface

1.1 倾斜均质黏性土坡沿直线滑裂面滑动的临界坡高

由黏聚力较小的黏性土组成的均质边坡,类似无黏土坡,可以假定滑裂面为直线面,如图1所示.当土体沿不连续直线滑裂面向下滑动时,形成刚性楔ABD,楔体的下滑速度为v,方向与滑裂面成 φ角(土体内摩擦角).外力所做功的功率等于土体自重W与速度v在垂直方向分量的乘积:

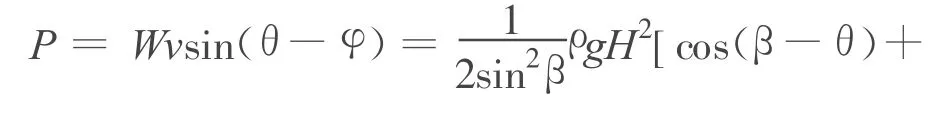
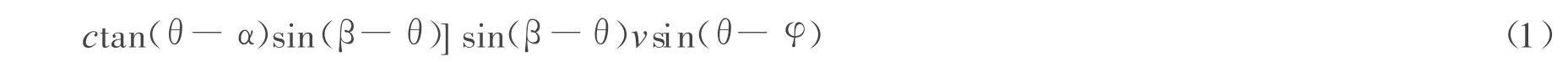
其中单位宽度土体自重为

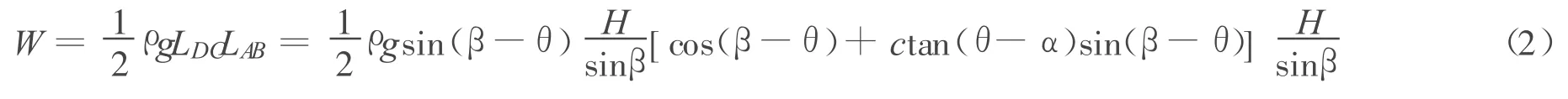
式中:ρ——土的密度;c——黏聚力;φ——内摩擦角.

土体沿不连续直线滑裂面滑动的内能耗散等于黏聚力与速度v在滑裂面上的分量v1的乘积:

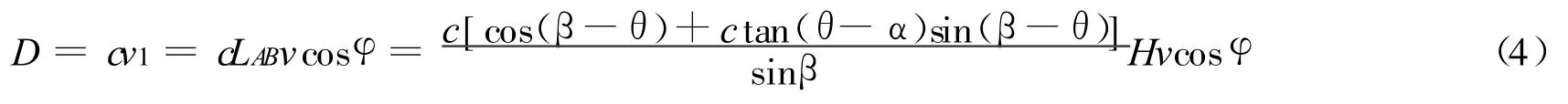
令外功率等于内能耗散率,有

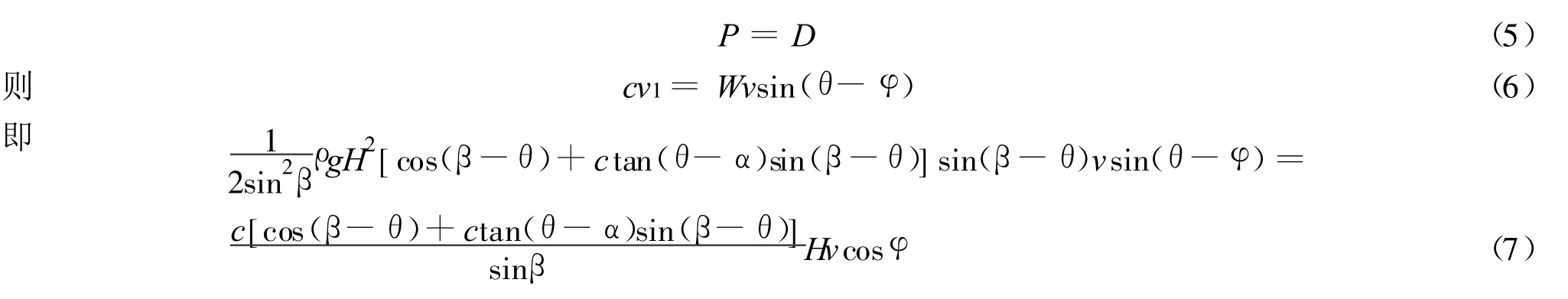
由此得到沿直线滑裂面破坏的临界坡高:

由式(9)得出结论:

a.无黏土或黏聚力较小的均质黏性土坡产生沿直线滑裂面的滑动时,影响临界坡高的主要因素是土体的抗剪强度、密度及坡体倾角β,而与坡顶面倾角α无关.

b.对于特定的均质黏性土坡,如果其 ρ,c,φ确定,则临界坡高H仅与坡体倾角β呈负相关关系,即边坡坡度愈缓,其临界坡高愈高.

c.当c=0时,Hc=0,说明对于无黏聚力的土体,边坡的任何高度都是不稳定的.

将β=π/2代入式(9),可以求得垂直边坡的最大高度

式(10)表明,对于上述均质直立土坡,如果土体的 ρ,c,φ为定值,则临界坡高Hc是一个定值.该类土坡的临界坡高与岩土体的内摩擦角和黏聚力正相关,与密度负相关.

1.2 倾斜均质黏性土坡沿对数螺线滑裂面滑动的临界坡高

一般均质黏性土坡产生滑动时,其滑面形态均为曲线,通常采用对数螺旋方程加以描述,图2为沿曲线滑裂面滑动示意图.

图2中的刚性土体A DB绕旋转中心O发生滑动时,AB面以下的土体保持静止,因此,滑动面AB是个速度不连续面.滑动土体ADB由于自重所做外功的功率可通过土块OAB,OA D,ODB所做外功功率之代数和求得;而沿AB面滑动土体所产生的内能耗散率则需要在整个表面积分而得.根据内外功率相等的原理,文献[7]经过推导整理后得

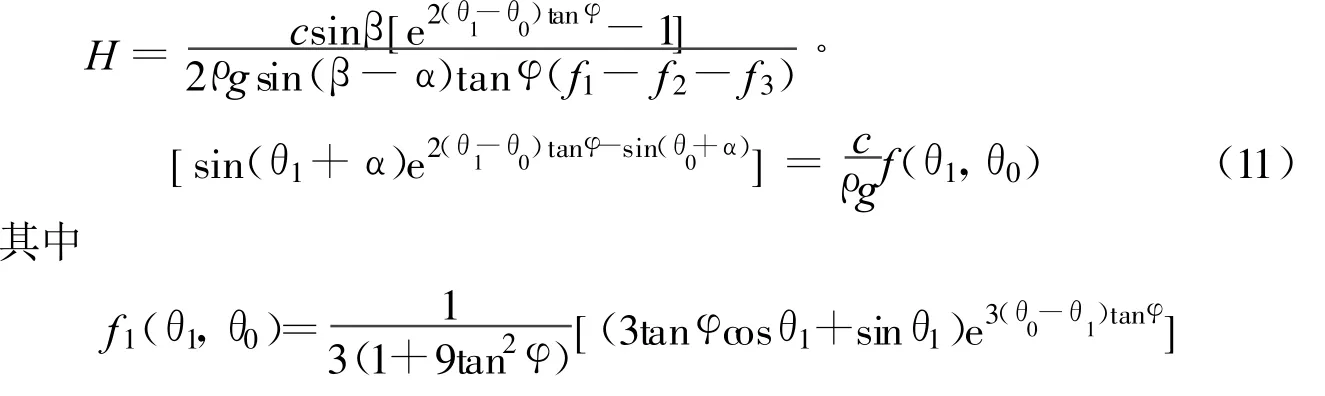
图2 对数螺旋滑裂面示意图Fig.2 Sketch of logarithmic spiral slip surface

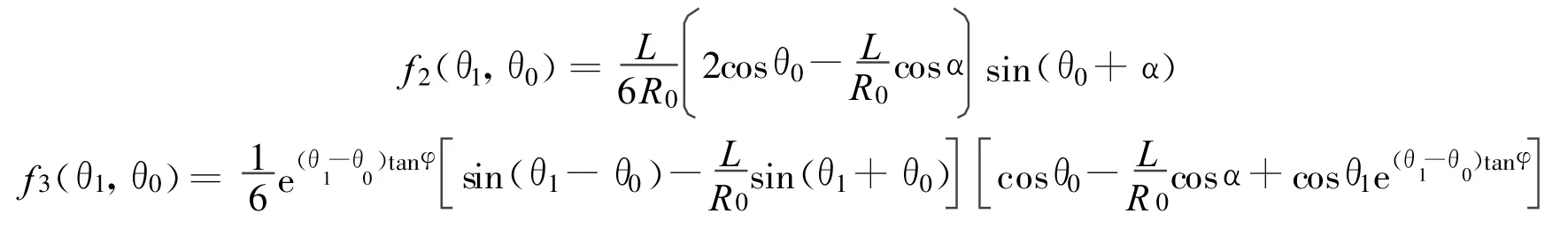
当滑动土体处于极限状态时,f(θ1,θ0)最小,故令求得 θ1,θ0后代入式(11)得土体的临界坡高:

由此可见,如果黏性土坡沿着对数螺旋面产生滑动,其临界坡高与土体的抗剪强度、密度、坡体倾角和坡顶的倾斜度都有关,因此计算过程复杂,只能通过查找文献[8]中的f(θ1,θ0)图表近似计算土体沿对数螺旋面滑动的临界坡高.

2 工程实例计算

2.1 工程概况

某市江南水乡度假村工程位于丘陵山坡场地,地表起伏大.施工过程中,一座5层的宾馆楼北侧存在几十米长的一段因采土而形成的高陡山坡,坡高3.5m左右,坡体呈10°以上的自然倾斜状态.受风化残坡积的影响,山坡表层是层厚3.0～5.0m的松软耕植土,色杂含块石,见植物根茎,土体的主要物理力学指标为:密度 ρ=1.85g/cm3,黏聚力c=10kPa,内摩擦角 φ=10°;表层土以下是厚度8.5～20.0m的含碎石黏土,呈硬塑状态,该土层渗透系数低、强度高.

建筑物的位置如图3所示,由于陡坡与建筑物的距离较近,所以探讨该边坡的稳定性对于建筑物的安全使用至关重要.

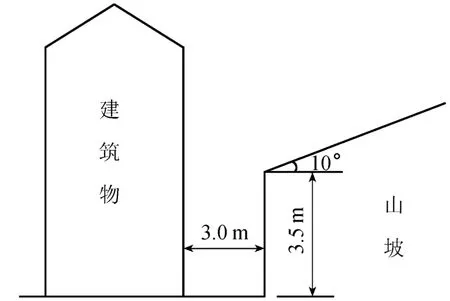
图3 建筑物位置示意图Fig.3 Sketch of location of building

2.2 土坡临界坡高的确定

该工程的直立边坡是山坡经过人工切坡后而导致的,具有土质均匀、黏聚力较小的特点,类似无黏土,所以,坡体一旦失稳将沿直线滑裂面滑动或者沿对数螺旋面滑动,下面分别加以探讨.

首先将 β=90°,α=10°,φ=10°,c=10kPa代入式(10)得H90°=2.58m.即该土坡沿直线滑裂面滑动的临界坡高为2.58m.

查阅文献[8]中的图表可知 ,当 β=90°,α=10°,φ=10°时,f(θ1,θ0)=4.47,代入式(12)得Hc=2.42m,即该土坡沿对数螺旋面滑动的临界坡高为2.42m.

以上计算结果表明,该直立边坡沿对数螺旋面滑动的临界坡高小于沿直线滑裂面滑动的临界坡高.从能量学的角度分析,一个处于极限平衡的土体将具有一定的滑动势能,同样势能的土体如果沿着曲线滑动时,滑动的土块范围广、质量大,相应的临界坡高小;而沿着直线滑动时,滑动的土块少、质量小,相应的临界坡高大.所以,一般情况下,黏性土坡的滑裂面呈曲线状,但是对于直立边坡,由于受临空效应的影响也会产生沿直线滑裂面的滑动.

上述分析说明该处的直立边坡是不稳定的,其自然直立高度远大于临界坡高,参照一些国内外学者的研究成果[9-12],应对本边坡进行合理的治理.

根据工程边坡高度小、坡顶平缓的特点,可以采用削坡减载加坡面植草防护的方式进行治理,削坡示意图如图4所示.为了保证边坡的稳定,削坡后坡体的临界坡高必须大于自然高度,所以应确定坡体的倾角 β.根据上述分析,该直立边坡沿对数螺旋面滑动的临界坡高小于沿直线滑裂面滑动的临界坡高,因此要先计算当坡体的自然高度与沿直线滑动的临界坡高相等时的坡

图4 削坡卸载示意图Fig.4 Sketch of cutting slope for unloading

体倾角,然后按两种滑动模式进行验算直到满足要求.

根据图4的三角关系得削坡后坡体的自然高度:

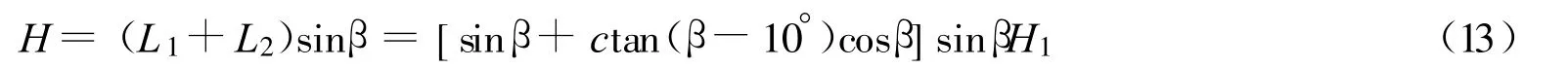
由图3可知,H1=3.5m.根据式(9),并进一步简化得土坡沿直线滑裂面的临界坡高:

当式(13)与式(14)相等时,满足

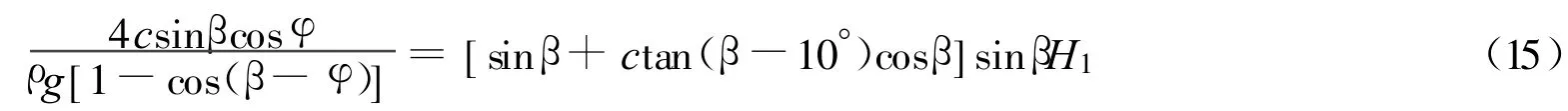
把H1=3.5m,c=10.0kPa,ρ=1.85g/cm3,φ=10.0°代入式(15)并用迭代法求得 β=73°.

该计算结果表明,当工程直立边坡削坡后的坡体倾角为73°时,边坡的自然高度刚好等于沿直线滑动的临界坡高,边坡处于极限平衡状态.根据边坡的临界坡高与坡角大小成反比的关系,坡体倾角 β应该小于73°,才能使边坡的自然高度小于临界坡高,满足边坡稳定条件,所以必须逐步验算 β.

首先取 β=70°,把 β=70°代入式(13)得到坡体的自然高度H=3.74m,然后把 β=70°代入式(14)得坡体沿直线滑裂面滑动的临界坡高为4.0m,说明边坡满足不产生直线滑裂面的滑动条件;用数据 β=70°,α=10°,φ=10°查文献[8]中的图表得f(θ1,θ0)=6.03,代入式(12)得到坡体沿对数螺旋滑裂面滑动的临界坡高为3.26m,该值小于边坡自然高度,说明边坡有可能沿对数螺旋面发生破坏,所以β=70°不能满足条件.

依次取 β为65°,60°进行验算后,均不能满足要求,最后设 β=55°代入式(13)得坡体的自然高度为4.00m;β=55°代入式(14)得边坡沿直线破裂面滑动的临界坡高为 5.95m;β=55°,α=10°,φ=10°查表并代入式(12)得坡体沿对数螺旋滑裂面滑动的临界坡高为4.08m.根据以上验算过程,当β=55°时,满足边坡的自然高度小于产生滑动的临界坡高的条件,可确保土坡稳定.因此该直立均质土坡的削坡角度要大于35°才能避免土体产生滑动.

3 结 论

a.由黏聚力较小的黏性土构成的均质土坡产生沿直线滑裂面的破坏时,其临界坡高与坡顶面倾角 α无关,只受土体的抗剪强度c和φ、密度ρ和坡体倾角β影响.

b.根据内外功率相等的原理,相同势能的土体沿着曲线滑动,由于曲线长而需要消耗更多的能量.因此,同样土体的均质黏性土坡产生沿对数螺旋滑裂面破坏的临界坡高小于直线滑裂面的临界坡高.

c.实际均质黏性直立土坡采用削坡护面的方法进行治理时,其合理削坡角度应满足按两种滑裂面计算所得临界坡高都大于土坡的自然直立高度这一条件.

[1]崔新壮,王爱营,刘雁冰,等.考虑岩土体变形的边坡临界高度上限解[J].山东大学学报:工学版,2006(5):73-76.(CUI Xinzhuang,WANG Ai-yin,LIU Yan-bing,et al.Upper-bound solution of critical height of slopeconsidering soil and rock deformation[J].Journal of Shandong University:Engineering Science,2006(5):73-76.(in Chinese))

[2]YU H S,SALGADO R,SLOAN S W,et al.Limit analysis versus limit equilibrium for slope stability[J].Journal of Geotechnical and Geoenvironmental Engineering,1998,124(1):1-11.

[3]XIE M,ESAKI T,ZHOU G,et al.GIS-based 3D critical slope stability analysis and landslide hazard assessment[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2003,129(12):1109-1118.

[4]张天宝.土坡稳定分析和土工建筑物的边坡设计[M].成都:成都科技大学出版社,1987.

[5]CHEN Jian,YIN Jian-hua,LEE C F.Upper bound limit analysis of slope stability using rigid finite elements and nonlinear programming[J].Journal of Geotechnical and Geoenvironmental Engineering,2003,40(4):742-752.

[6]CUI X Z,JIN Q,SHANG Q S,et al.General solving method of energy dissipation rate of deforming region in upper-bound analysis for Coulomb material[J].Key EngineeringMa-terials,2006(6):1439-1444.

[7]YU Mao-hong.Unified strength theory and itsapplications[M].New York:Springer,2004.

[8]黄仰贤.土坡稳定分析[M].北京:清华大学出版社,1988.

[9]DONALLD I,CHEN Zu-yu.Slope stability analysis by the upper bound approach:fundamentals and methods[J].Canadian GeotechnicalJournal,1997,34(6):853-862.

[10]盛维高,李国维,袁俊平.基于含水量变化对土体强度影响的高边坡稳定分析[J].水利水电科技进展,2009,29(1):12-15.(SHENG Wei-gao,LI Guo-wei,YUAN Jun-ping.Stability analysis of high slopes based on the influence of water content change on soil strength[J].Advances in Science and Technology of Water Resources,2009,29(1):12-15.(in Chinese))

[11]蒋忠信.边坡临界坡高卡尔曼公式之工程应用[J].岩土工程技术,2007(5):217-220.(JIANG Zhong-xin.Engineering application of Culmann's formula on critical height of slope[J].Geotechnical Engineering Technique,2007(5):217-220.(in Chinese))

[12]张玉,张方方.变水位多工况下大型渠道土质边坡的稳定分析[J].水利水电科技进展,2010,30(1):56-60.(ZHANG Yu,ZHANG Fang-fang.Stability analysis of soil slopes for large-scale canals considering variable water levels and various working conditons[J].Advances in Science and Technology of Water Resources,2010,30(1):56-60.(in Chinese))