矩形采砂坑形态对明渠水位降低的影响
2011-07-11张九鼎李开杰
肖 洋,张九鼎,雷 鸣,李开杰,4
(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.河海大学水利水电学院,江苏南京 210098;3.河海大学水资源高效利用与工程安全国家工程研究中心,江苏南京 210098;4.国家防汛抗旱总指挥部办公室,北京 100053)
河道无序采砂使河床形态发生较大的改变,进而对河道水位、主流流路和河势稳定等产生影响,危及河流的防洪、航运和供水安全,因而河道采砂问题日益受到研究者们的重视和关注[1].
为了解采砂坑对河道的影响,前人开展了大量的研究,重点主要集中在采砂坑对河道水流特性[2-3]和冲淤演变[4-11]的影响等方面,如毛劲乔[2-3]采用各向异性三维代数应力模型研究了采砂坑附近水流形态、横向次生流和紊动特性的变化;李健等[4-5]采用平面二维水砂数学模型研究了不同采砂坑对河床演变的影响.由于明渠水流自由表面模拟的复杂性,目前在采砂坑形态对明渠水位降低的影响方面研究很少.本文应用计算流体力学商业软件FLUENT,建立了明渠立面二维数学模型,研究了不同矩形采砂坑长度、深度和面积对水位跌落的影响.
1 数学模型
1.1 控制方程
控制方程采用不可压缩常密度雷诺平均Navier-Stokes(N-S)方程组:连续方程

动量方程

式中:ρ——流体密度;t——时间;u,v——x,y方向上的流速——x,y方向上的脉动流速;ν——运动黏性系数.封闭方程采用标准k~ε模型的紊流方程.
1.2 VOF方法
VOF方法(volume of fluid method)[12]是一种有效模拟水流自由表面的方法,它利用计算网格单元中流体体积量的变化与网格单元本身体积的比值函数来确定自由表面位置和形状,可处理自由表面重入等非线性现象,具有计算时间短、存储量少等优点.VOF法以压力p和速度u,v作为独立原始变量,根据各个时刻流体在网格单元中所占体积函数F来构造和追踪自由面,若在某时刻网格单元中F=l,则说明该单元全部为指定相流体所占据,为流体单元;若F=0,则该单元全部为另一相流体所占据,相对于F=1流体称为空单元;当0<F<l时,则该单元为包含两相物质的交界面单元.
1.3 计算区域和计算条件
建立的采砂明渠立面二维数学模型计算区域及网格剖分见图1,其中坐标原点位于上游进口,x为水流方向,y为垂向.采砂明渠总长为50m,计算区域采用四边形非均匀结构化网格剖分,其中,普通明渠段网格大小为4cm×1.5cm,砂坑上方明渠段网格3cm×1.5cm,砂坑处网格大小为3cm×1 cm,共生成网格93622个.砂坑布置在距进口15m处,底壁为定床,底壁粗糙高度为2mm,明渠底坡取0.1%.采砂坑尺寸组成共9种,见表1.由于缺乏含采砂坑明渠的实验验证资料,选用文献[13]中的部分明渠水流实验数据(表2)检验数学模型的正确性.采砂坑对明渠水位降低影响的计算条件为:进口单宽流量为0.5m2/s,进口流速为1m/s,水深为0.5m,弗劳德数为0.45.

图1 采砂坑计算区域及网格剖分Fig.1 Computational area and grid generation of sandpit
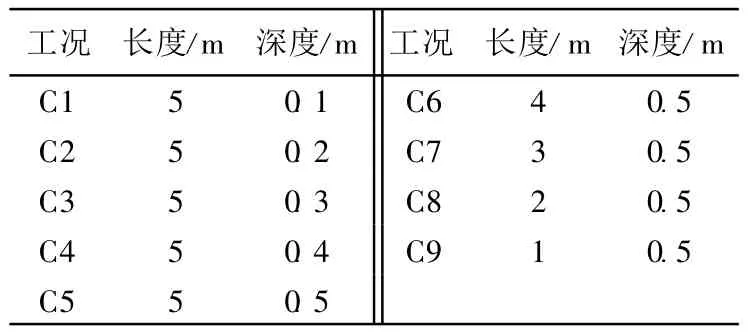
表1 不同采砂坑模型参数Table 1 Model parameters of different sandpits

表2 明渠流计算条件Table 2 Computational parameters of open channel flow
1.4 边界条件
进口分为空气进口和水流进口两部分.水流进口设为速度进口边界条件,给定水流平均流速、紊动能和紊动动能耗散率.空气进口设为压力进口边界条件,各参数取值与水流进口相同.出口为压力出口边界条件,给定出口自由水面高度,考虑出口紊流已充分发展,设其湍动能k和紊流耗散率ε与水流进口相同.区域顶部边界采用压力出口边界条件,与空气进口相同.固定壁面采用标准壁面函数法模拟.
1.5 求解方法
二维N-S方程的求解采用有限体积法(finite volume method),求解器为分离式求解器,并采用隐式方案实现线性化过程.方程离散时,压力速度耦合方式选择PISO算法,压力的插值格式采用body force weighted格式,动量等的离散格式采用二阶迎风(second order upwind)格式.当各变量残差小于0.0001或出口质量流量变化小于0.5%时,认为计算收敛.
2 模型验证
明渠水流的模拟结果与Tominaga等[13]的实验数据对比见图2,图2(a)为垂线流速分布对比,图2(b)为紊流强度u′/u*沿垂线分布对比.由图2(a)可见,垂线流速分布的计算值与实验值吻合较好,即内区(y/h<0.6的区域),流速符合对数分布规律,在外区(y/h>0.6的区域),其流速分布偏离对数分布,在自由水面附近,垂线流速略有减小.由图2(b)可以看出,紊流强度随着水深的增加而减小,计算值与实验值基本吻合.
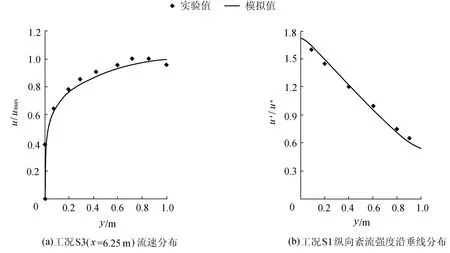
图2 模拟结果与实验值对比Fig.2 Comparison of simulated results and experimental results
3 计算结果分析
3.1 水位变化
河道内采砂坑形成后,水位将会出现跌落(图3).图4和图5分别为不同采砂坑深度、长度下最大水位跌落变化情况(图中,h为坑前水深,Δh为水位降落,H为采砂坑深度,Δh/h为相对水位降落值,H/h为相对采砂坑深度,L为采砂坑长度,L/H为长深比).
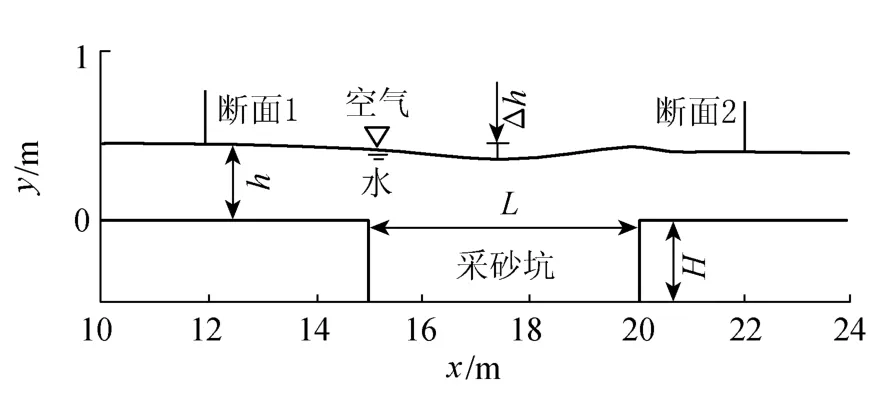
图3 水位降落示意图Fig.3 Schematic diagram of drawdown

图4 相同采砂坑长度下相对采砂深度与水位降落关系Fig.4 Relationship between relative depth and drawdown with same length of sandpit
由图4可见,随着采砂坑深度的增大,最大水位降落逐渐增加,整个曲线可以分为3段,当采砂坑深度较小时,即H/h≤0.45时,水位降落随着采砂坑深度的增大缓慢增加,这与李健等[5]的计算结果相近;当采砂坑深度增大到一定程度后,即0.45<H/h≤0.9时,随着采砂坑深度的增大水位降落值快速增大;当采砂坑深度继续增大,即H/h>0.9时,水位降落的增幅再次趋于平缓,此时采砂坑深度的增大对水位降落的影响逐渐减小.由图5可见,随着采砂坑长度的增大,水位降落的变化与图4呈相近的趋势,仅是幅度有所不同.
图6为采砂坑面积与水位降落关系,由图6可见,随着采砂坑面积的增大,水位降落均呈缓慢增大、急剧上升、再趋于平缓3个变化阶段,当采砂坑面积相同时,长深比越大,水位降落越明显,即采砂坑长度对水位降落的影响大于深度的影响.

图6 采砂坑面积与水位降落关系Fig.6 Relationship between sandpit's area and drawdown
3.2 流线变化
图7为计算的各典型工况流线,其中,图7(a)(b)(c)为坑长为5m时,不同采砂坑深度情况下的流线变化,水流在采砂坑的前部形成一个涡旋.当坑深较小时,如H=0.1m,涡旋很小,约为0.015m2,相应的能量损失较小;随着采砂坑深度的逐渐增加,涡旋的尺寸也逐步变大,相应的能量损失也增大,当坑深为0.5m时,涡旋尺寸增大到0.84m2.图7(c)(d)(e)(f)为坑深为0.5m时,不同采砂坑长度情况下的流线变化,随着采砂坑长度的增加,流线形成的涡旋面积也逐渐增大,但当坑长大于4m后,涡旋面积变化幅度较小.
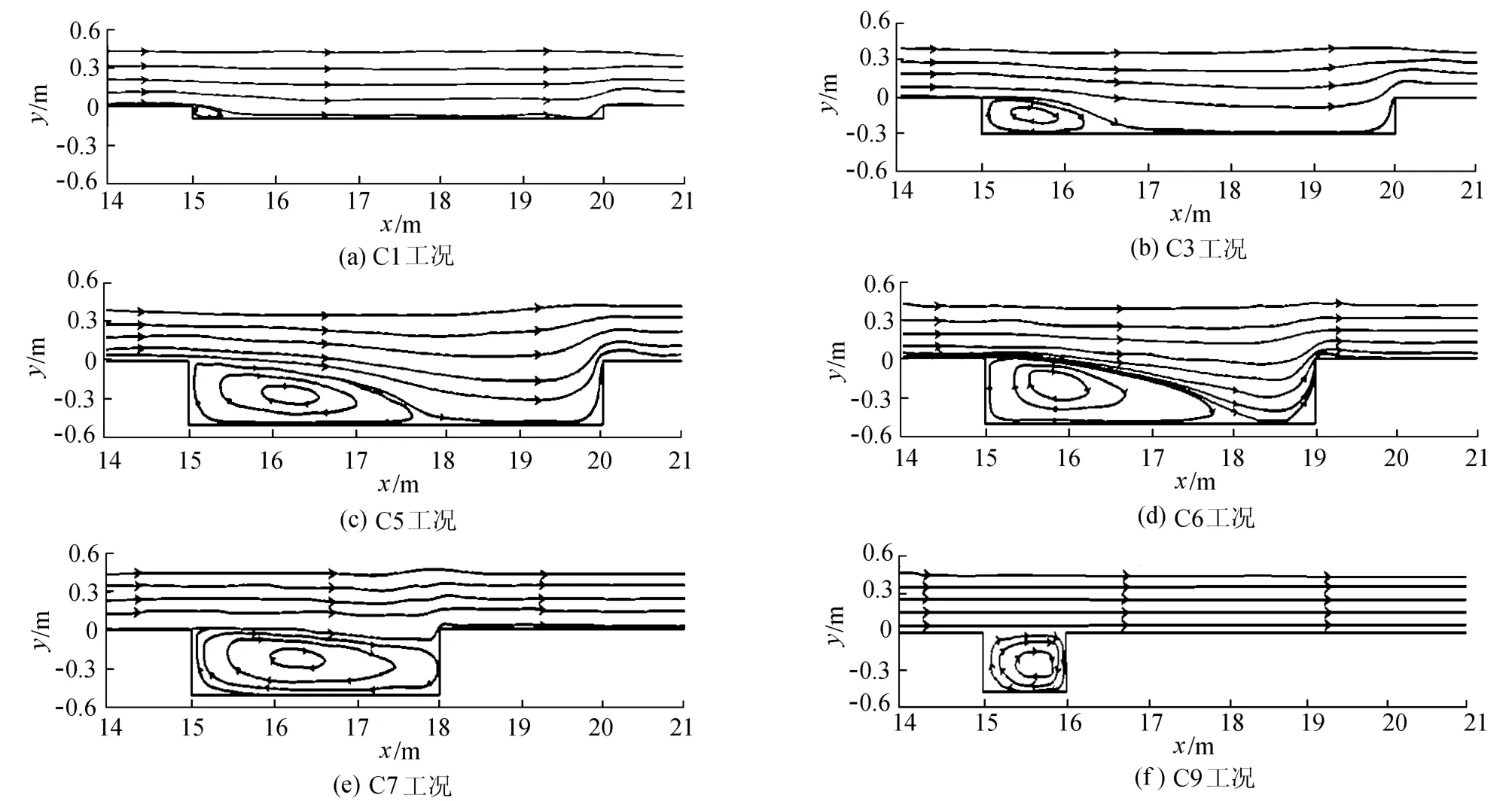
图7 模型计算的各典型工况流线Fig.7 Streamlines in typical conditions computed by model
3.3 能量损失分析
如图3所示,取采砂坑前后流速分布均匀的断面1(x=12m)和断面2(x=22m),能量方程可写成:
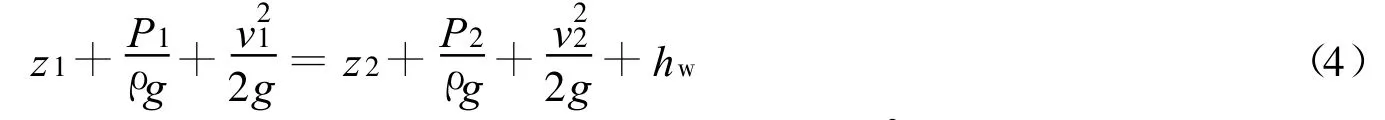

图5 相同采砂坑深度下长深比与水位降落关系Fig.5 Relationship between length-depth ratio and drawdown with same depth of sandpit
式中:z1+P1/ρg——断面1处测压管水头;z2+P2/ρg——断面2处测压管水头;v21/2g——断面1处流速水头/2g——断面2处流速水头;hw——采砂坑前后断面的能量损失.基准面取采砂坑底部.
建立相对采砂坑深度与单位深度局部水头损失的关系(图8,图中hw/H为单位坑深局部损失)和相对采砂坑长度与单位长度局部水头损失的关系(图9,图中hw/L为单位坑长局部损失,Lmax为最大采砂坑长度).为了同时对比单位深度和长度局部水头损失与水位降落的关系,图8、图9还点绘了水位降落值与相对采砂坑深度和长度的关系.

图8 坑深与局部水头损失、水位降低关系曲线Fig.8 Relationships curves between sandpit's depth,local head loss,and drawdown

图9 坑长与局部水头损失、水位降低关系曲线Fig.9 Relationships curves between sandpit's length,local head loss,and drawdown
由图8和图9可见,坑深和坑长变化对局部水头损失的影响规律相近,即当坑深、坑长为零时,不考虑沿程损失,局部水头损失几乎为零;随着坑深、坑长尺度的增大,出现涡旋,局部水头损失急剧增大;当坑深、坑长继续增大,局部水头损失逐渐减小,并趋于平缓.这种变化规律与水位降落的变化基本一致,在局部水头损失急剧增大阶段,水位降落平缓增大;在局部水头损失增加至最大值时,对应着水位降低值急剧上升的起点;在局部水头损失降低阶段,水位降低值急剧上升;在局部水头损失趋于平稳后,水位降低值也趋于平稳.
4 结 论
a.当采砂坑面积相同时,在一定范围内,长深比越大,水位降落越明显,采砂坑长度的增加对水位跌落影响较大.
b.随着采砂坑深度、长度增大,坑内水位跌落值呈现缓慢增加、急剧增大和再平缓增大3个阶段,对应的局部水头损失呈现急剧上升、急剧下降、缓慢下降3个阶段.
[1]曾慧俊,谈广鸣,吕平.采砂河道数值模拟研究进展[J].南水北调与水利科技,2008,6(2):80-83.(ZENG Hui-jun,TAN Guangming,LV Ping.Development of the research on numerical model for sand-digging watercourses[J].South-to-North Water Transfers and Water Science&Technology,2008,6(2):80-83.(in Chinese))
[2]毛劲乔.顺直河道采沙坑水流的三维数值模拟[J].水动力学研究与进展:A辑,2003,18(5):660-666.(MAO Jing-qiao.3-D numerical modeling of flow around sand pit on straight riverbed[J].Journal of Hydrodynamics,2003,18(5):660-666.(in Chinese))
[3]毛劲乔.河道复杂采沙坑附近流场的数值模拟[J].水科学进展,2004,15(1):6-11.(MAO Jing-qiao.Numerical simulation study of flow field around the sandpit with complicate shape in riverbed[J].Advances in Water Science,2004,15(1):6-11.(in Chinese))
[4]李健,杨文俊.顺直河道采沙效应的平面二维数值模拟[J].人民长江,2008,39(2):52-54.(LI Jian,YANG Wen-jun.2-D numerical modeling of flow around sand pit on straight riverbed[J].Yangtze River,2008,39(2):52-54.(in Chinese))
[5]李健,杨文俊,陈辉.不同条件下矩形沙坑影响的数值模拟对比研究[J].泥沙研究,2009(6):74-80.(LI Jian,YANG Wen-jun,CHEN Hui.Numerical simulation on effect of rectangular sand-pit on channel bed variation[J].Journal of Sediment Research,2009(6):74-80.(in Chinese))
[6]MACDONALOD A.Predicting channel recovery from sand and gravel extraction in Naugatuck River and adjacent floodplain[C]//Proceedings of the 1988 National Conference on Hydraulic Engineering.USA:Colorado Springs,1988:702-707.
[7]KUBICKI A,MANSO F,DIESING M.Morphological evolution of gravel and sand extractionpits,Tromper Wiek,Baltic Sea[J].Estuarine,Coastal and Shelf Science,2007,71(3/4):647-656.
[8]毛野.初论采沙对河床的影响及控制[J].河海大学学报:自然科学版,2000,28(4):92-96.(MAO Ye.A study on the effect of sand gravel extraction on riverbed and its control[J].Journal of Hohai University:Natural Sciences,2000,28(4):92-96.(in Chinese))
[9]毛野,黄才安.采砂对河床变形影响的试验研究[J].水利学报,2004,35(5):64-69.(MAO Ye,HUANG Cai-an.Experimental study on effect of sand mining on riverbed deformation[J].Journal of Hydraulic Engineering,2004,35(5):64-69.(in Chinese))
[10]毛野,黄才安,陈建华,等.长江镇江段河道采砂的影响及其控制利用的试验研究[J].泥沙研究,2004(3):41-45.(MAO Ye,HUANG Cai-an,CHEN Jian-hua,et al.Experimental study on the effects of sand mining on the riverbed deformation in Zhenjiang reach and its application[J].Journal of Sediment Research,2004(3):41-45.(in Chinese))
[11]穆锦斌,杨芳丽,谢作涛,等.采砂工程对河道影响分析研究[J].泥沙研究,2008(2):69-76.(MU Jing-biao,YANG Fang-li,XIE Zuo-tao,et al.Effect of sandmining project on the river channel[J].Journal of Sediment Research,2008(2):69-76.(in Chinese))
[12]张健,方杰,范波芹.VOF方法理论与应用综述[J].水利水电科技进展,2005,25(2):67-70.(ZHANG Jian,FANG Jie,FAN Boqin.Advances in research of VOF metho[J].Advances in Science and Technology of Water Resources,2005,25(2):67-70.(in Chinese))
[13]TOMINAGA A,NEZU I.Three-dimensional turbulent in straight open channel flows[J].Journal of hydraulic research,1989,27(1):149-173.
