钢管饱和磁化下涡流检测有限元仿真研究

万本例，张路根，胡 智，宋 凯，任吉林

（1.南昌航空大学 无损检测技术教育部重点实验室，南昌 330063；2.江西省锅炉压力容器检验检测研究院，南昌 330029）

0 引言

涡流检测作为一种重要的无损检测方法，在核电、石油、航空等领域应用广泛，而对非铁磁性管道的检测，涡流检测技术的应用已经非常成熟，但在铁磁材料实施涡流检测时，由于磁导率的波动引起涡流检测中有较大的噪声信号，以至于难于检测出缺陷，因此一般采用远场涡流检测或通过对铁磁管道进行饱和磁化的方式，以降低其磁导率等影响，再实施涡流检测。然而与非铁磁性材料相比，铁磁材料具有独特的特性，并非是非铁磁性材料检测机理的简单延伸，因此钢管磁饱和的涡流检测磁特性影响机理对缺陷的定量评定有重要意义。

目前国内外在非铁磁材料涡流检测研究较多，但饱和磁化下涡流检测的研究较少，康宜华等[1,2]对饱和磁化下涡流检测的原理有进一步的认识，并在理论计算和试验仿真的基础上证明饱和磁化下涡流检测存在漏磁和涡流两种效应；林俊明等[3]在钢管涡流检测实践中发现钢管过饱和磁化后涡流检测会出现内外壁缺陷信号相位无法分辨的问题。B.Helif[4]等发现铁磁材料在热处理和表面处理后其表面缺陷仍能够通过涡流检测发现；A.V.SUKHIKH等[5]通对比分析了磁饱和前后钢管的涡流检测信号。

本文建立了钢管饱和磁化的内插式涡流检测的有限元模型，以矩形槽表征裂纹类缺陷，提出了两种模型间磁导率处理的方式，计算了磁化后铁磁管道的磁导率分布，以及磁化后对管道进行涡流检测时线圈的阻抗的变化，从信号相位和幅值上分析了磁导率和缺陷对阻抗信息的影响，以期对铁磁材料涡流检测的工程实践具有指导作用。

1 仿真模型的构建

1.1 饱和磁化涡流检测有限元模型

图1是内插式涡流探头检测饱和磁化后铁磁管道的涡流检测模型，考虑模型的对称性，使用2D轴对称模型替代三维实体模型。被检管道内径D为56mm，壁厚H为2mm，长度L为160mm。直流磁化线圈内径D1为66mm，外径D2为72mm。涡流检测线圈内径d1为52mm，外径d2为55mm，线圈宽度ι为1.5mm，间距d为1.5mm。管内充满空气，管外自由区建模时设置了圆柱环形空气，空气层厚度为30mm。管壁缺陷为矩形槽以模拟裂纹类缺陷，且为管外壁周向刻槽。缺陷如图1所示，矩形槽宽度c为1mm，深度h为1mm。检测管道磁导率由B-H曲线给出，电导率为1.03×106S/m；磁化线圈的相对磁导率为1，电导率为0.58×108S/m。涡流检测线圈的相对磁导率为1，电导率为0.58×108S/m；线圈匝数N为500匝。

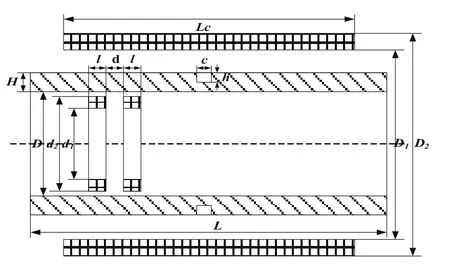
图1 饱和磁化涡流检测有限元模型

1.2 饱和磁化涡流检测有限元仿真方法

如图2所示，在饱和磁化涡流检测有限仿真的过程中，采用直流线圈对管道进行一次磁化，通过对比来研究管道磁化后的状态对涡流检测的影响，最后分析阻抗差异得出结论。在磁导率的处理问题上，对已经划分好有限元网格的管壁，通过单元表操作命令[6]，按照管壁网格单元序号，依次提取磁化后每个单元的磁导率值，并把这些值保存在数组中，在后面的涡流检测模型中，保证管壁、缺陷、空气层与磁化模型参数的一致性，尤其是对于管壁和缺陷网格两者是一致的，这就排除了计算引起的误差以及便于磁导率的重新赋予，并做到了磁化后管道材料参数与涡流检测时管道材料参数的不变性。

图2 饱和磁化涡流检测有限元仿真方法

2 仿真结果讨论分析

2.1 直流磁化结果

当单线圈激励面电流密度为3.5×107A/m2时，如图3a所示，缺陷为矩形槽缺陷，宽度和深度都为1mm，在管道外表面提离0.5mm处，沿缺陷中心前后各取10mm，拾取径向和轴向的磁通密度值，其采样点数为300个。由此可知，经过磁化后的铁磁性管道会在缺陷处产生漏磁通且会影响管壁的磁导率分布，尤其是在缺陷附近，其磁导率会产生不均匀性分布，如图3b所示，通过ANSYS仿真观察磁化后管壁的磁导率分布，整个管壁范围的磁导率都下降很多，其在矩形缺陷底部相对磁导率由最高值600下降到平均值为6左右，如图3b中的蓝色区域，但在矩形缺陷两翼，磁导率还是比较大，只下降了几百单位左右，这就导致了磁导率在管壁磁化后的不均匀分布。

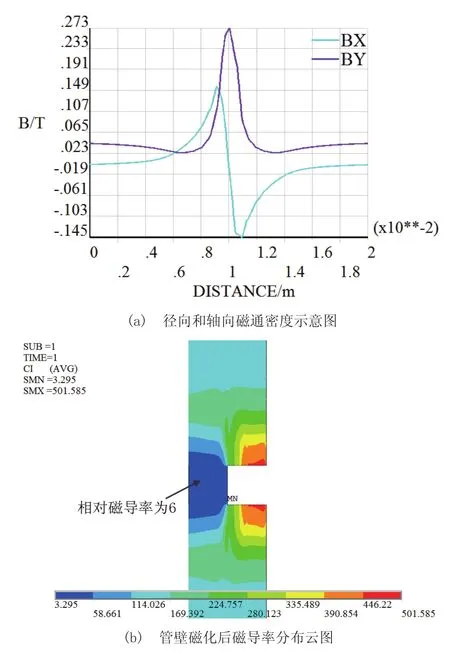
图3 宽度为1mm、深度为1mm缺陷管壁磁化状态示意图

2.2 磁化后涡流检测结果

建立如图2所示涡流检测仿真模型，当激励频率为10kHz，缺陷深度为1mm、宽度为1mm时，将2.1磁化后管壁所得的磁导率参数按照磁化模型管壁的单元序号依次赋予涡流检测模型中管壁。由此模型，反映了磁化后管壁的磁导率状态，进而进行涡流检测；另提取管壁缺陷下方磁化后的磁导率（相对磁导率为6），以此磁导率作为管道的材料参数进行涡流检测仿真，同时保证管道、缺陷、空气、网格的不变，由同一管道不同磁导率状态下的涡流检测信号可得图4所示阻抗信号图，黑色“8字”图形反应了磁化后磁导率不均匀性和缺陷引起的涡流检测信号，其阻抗相位角为85.26o，幅值为29.27Ω；红色“8字”图形反映了磁化后缺陷下方某一磁导率（相对磁导率为6）和缺陷引起的涡流检测信号，其阻抗相位角为146.9o，幅值为4.412Ω，可见两者差别挺大，并不相同。

图4 磁化后涡流检测阻抗图

2.3 无缺陷时磁化后涡流检测结果

按照2.2相同的方式处理磁化后管壁的磁导率，对无缺陷的管壁，待赋予磁导率参数后，进行一次涡流检测，涡流检测信号如图5所示，并无明显的“8字”形信号，而是近似一条直线。将图4中含有磁导率不均匀性和缺陷两种因素影响的涡流检测信号与图5中的涡流检测信号进行差分，所得结果如图6所示，可以得到一个完整的“8字”形涡流检测阻抗信号图，其涡流阻抗相位角为85.26o，幅值为29.25Ω，由此可知，当管道被磁化后，对管壁进行涡流检测时，即使无缺陷，管壁磁化后的状态还是对涡流检测信号有一定的影响的。

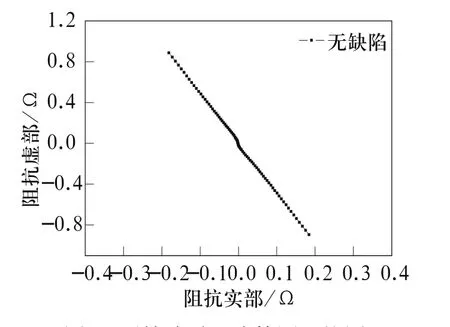
图5 无缺陷时涡流检测阻抗图

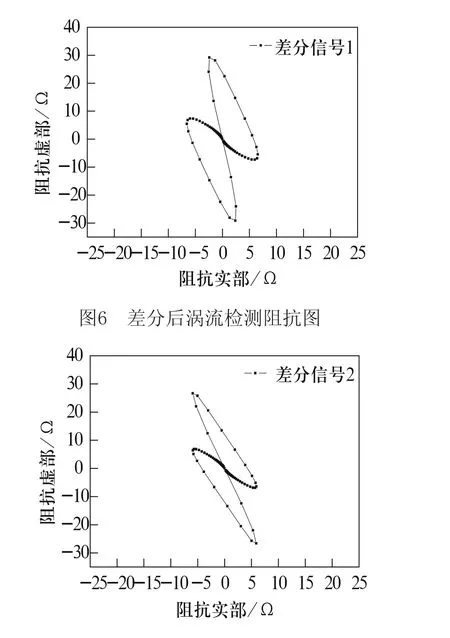
图7 磁导率影响下涡流检测阻抗图

将图6中阻抗信号与图4中红色“8字”阻抗信号进行差分所得结果如图7，这都是仅由磁化后磁导率不均性引起的涡流阻抗信号，其涡流阻抗相位角为77.49o，幅值为27.29Ω，不同于缺陷引起的涡流阻抗信号。可见磁导率不均性对涡流阻抗信号的影响还是比较大的，由此信号可能会对缺陷的判定产生一定的影响，导致缺陷的误判。

3 结论

1）通过有限元仿真可知，当铁磁管道被磁化后，管壁的磁导率有显著的下降，但因管壁上缺陷的存在又会使磁化后管道的磁导率产生不均匀性分布，且在缺陷周围磁导率比远离缺陷管壁磁导率大很多。

2）对饱和磁化后的管道进行涡流检测时，涡流阻抗信号是由磁化后磁导率不均匀性和缺陷共同作用引起，且磁导率对涡流阻抗信号影响比缺陷大很多，这就有可能导致缺陷误判。

3）当管道无缺陷时，管道磁化后的状态还是对涡流检测阻抗信号有一定影响的，但对幅值和相位影响不大。

[1] 康宜华,宋凯,任吉林等.磁饱和后的涡流检测信号的非涡流效应[J].无损检测,2009,31(4):257-260.

[2] 宋凯,康宜华,等.漏磁与涡流复合探伤时信号产生机理研究[J].机械工程学报,2009,45(7):233-237.

[3] 林俊明,赖传理,任吉林.钢管涡流探伤中缺陷信号的相位分辨[J].无损检测,2011,33(1):2-8.

[4] Helifa B,Oulhadj A,et al.Detection and measurement of surface cracks in ferromagnetic materials using eddy current testing[J].IEEE TRANSACTIONS ON MAGNETICS, 2003,39(3):1527-1530.

[5] SUKHIKH AV.Application of the magnetic saturation method for eddy-current inspection of spent fuel elements from fast reactors[J].Atomic Energy,2007,102(2):139-145.

[6] 龚曙光,谢桂兰.ANSYS操作命令与参数化编程[M].北京:机械工业出版社,2003.