形状可变救助型机器人的结构及其越障能力的分析与实验

张 勤，王曼莉，黄小刚，余晓鑫，田联房

（1.华南理工大学 机械与汽车工程学院，广州 510640；2.深圳市特种设备安全检验研究院，深圳 518029；3.华南理工大学 自动化科学与工程学院，广州 510640）

0 引言

近年来多发的自然灾害如地震、火灾、洪水等，人为的恐怖祸害如恐怖活动、武力冲突等严重危害着人们的安全。在这种紧急而危险的救援工作中，救助型机器人起着越来越重要的作用[1]。它们的参与可以有效地提高救援效率，减小灾难的损失。现有的救灾机器人移动机构主要有：无肢运动（以蛇形运动为主）、轮式、腿式、轮腿式和履带式等。其中，蛇形机器人具有运动稳定性好，适应地形能力强和牵引力高等特点，但多自由度控制困难，运动速度低；轮式机器人具有结构简单，重量轻，轮式滚动摩擦阻力小和机械效率高等特点，但越过沟渠、台阶的能力差；腿式机器人具有适应地形能力强的特点，能越过大的沟壕和台阶，其缺点是稳定性差，速度慢；轮腿式机器人融合了腿式机构的适应地形能力和轮式机构的高速高效性能，其缺点是结构相对复杂；履带式机器人地形适应能力强，但要越过大的沟壕，自身的尺寸就要做得很大，能耗大。这些机器人的移动机构有各自的优势，但翻越相当于自身高度的障碍的能力都较差[2～4]。本文提出了形状可变/多方位驱动救助型机器人的结构，它兼有蛇形机器人和履带式机器人的优点，可以根据灾难现场的情况，改变其形状，调整其姿态，实现上、下楼梯，翻越障碍物，跨越沟壑，从沟壑中脱出等功能，从而胜任瓦砾和废墟等恶劣路面上行走。在此基础上，本文详细分析了该机器人翻越台阶、楼梯典型障碍的运动过程及其最大越障能力；讨论了形状可变救助型机器人结构的重量配置布局、越障过程中机器人的形状，各面姿态等因素对越障能力的影响；提出了形状可变救助型机器人在典型障碍下的越障策略，并通过实验验证了所提策略的可行性。

1 形状可变救助型机器人的结构

形状可变救助型机器人兼有履带式机器人和蛇形机器人的特点。它由五个面组成，如图1所示，即四个侧面和一个中心面。各个侧面与中心面之间通过转动轴连接，使得各个侧面相对于中心面可以自由转动，进而可以改变机器人的形状。机器人每个面上分别安装独立的履带式移动机构，且履带式移动机构与其相连接的面之间可以相对转动，使得机器人能自由地改变运动方向，实现多方位驱动[5,6]。这种结构的救助型机器人可以根据灾害现场的情况，通过改变各个面之间的相对姿态，变换机器人的形状，实现在瓦砾和废墟等恶劣路面上的移动。例如：狭窄，低矮的地方，各面伸展成扁平型通过，如图2所示；平坦的地方，各个面闭合，缩成小立方体行走；跨越沟壕时，可以展成蛇形，如图3所示；由于各个面上都安装有履带，使其不怕滚落和翻倒，无论其哪个面与地面接触，都能正常移动，不需要将机器人恢复到可行走面，如图4所示[6,7]。机器人的驱动轮的数目也可以选择，使其在满足运动要求的前提下，节省能耗[8]。

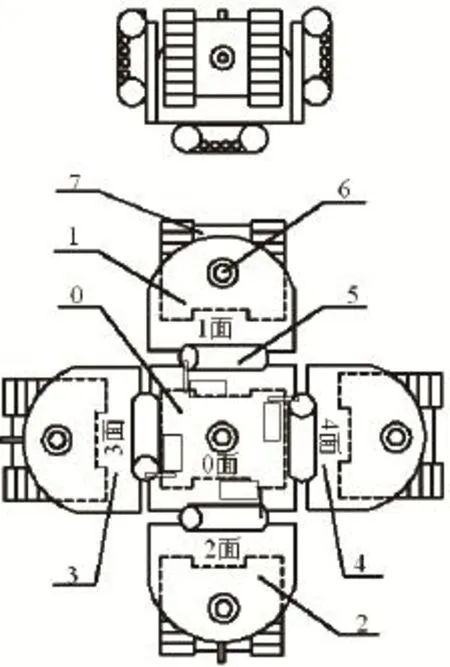
图1 形状可变救助型机器人机械结构简图

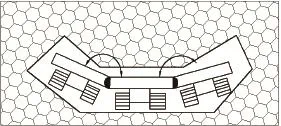
图2 机器人进入低矮地方的示意图

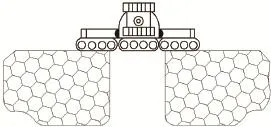
图3 机器人跨越沟壕的示意图

图4 机器人滚落、翻倒后继续正常行驶的示意图

2 越障能力分析

越障性能是影响救助型机器人运动能力的重要因素之一。机器人在复杂地形中运动，会遇到各式各样的障碍物，包括斜坡、台阶、凸台、沟壕、楼梯及这些障碍的组合等。这就要求机器人必须具备很强的越障能力，使机器人不但能够翻越这些障碍，还能保持越障过程中的稳定性。形状可变救助型机器人可以根据障碍物的特点，变换形状，调整各面的姿态，使其在越障过程中，各面分别发挥支撑，攀爬等不同的功能，以使机器人最大限度地发挥其越障能力，稳定地翻越障碍物。下文以翻越台阶和楼梯为例对形状可变救助型机器人的越障能力进行分析。

2.1 翻越台阶能力分析

形状可变救助型机器人翻越台阶时，为了提高其越障过程中的稳定性，机器人的各个面展开成扁平状，使其重心降低。其中面0，3，4在同一平面上，面1，2根据翻越的过程，变换其姿态。翻越台阶时机器人姿态和受力如图5(a)所示。为了成功翻越台阶，机器人的整体重心（ZMP）位置必须位于履带与台阶的接触点的前方。考虑能够翻越台阶的临界状态,机器人的整体重心应在台阶与机器人履带接触点M的垂线延长线PM上，由机器人各面的几何关系和临界越障姿态的静力学方程可得：

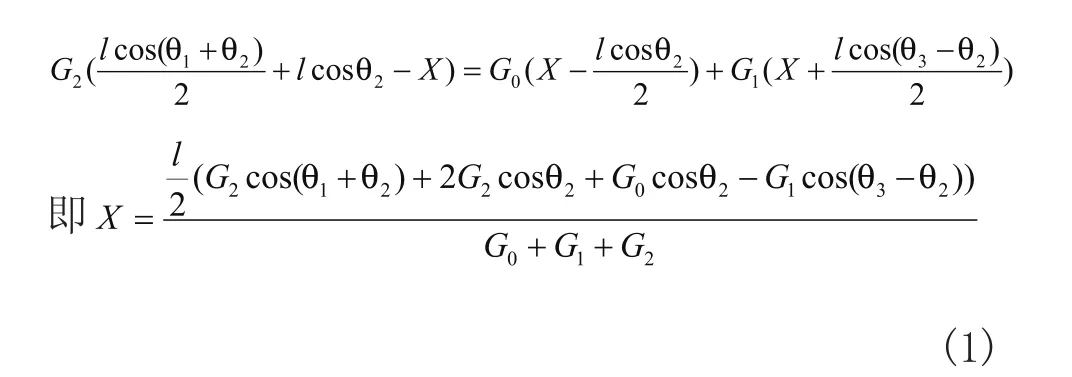
式中X为机器人的整体重心与中心面攀爬段之间的水平距离，ι为面0的边长，G0、G1、G2分别为面0，3，4、面1、面2面板及其附属机构的重量， θ1为面2相对于面0所偏转的角度，θ2为面0与台阶水平方向所成的角度，θ3为面0相对于面1所偏转的角度。

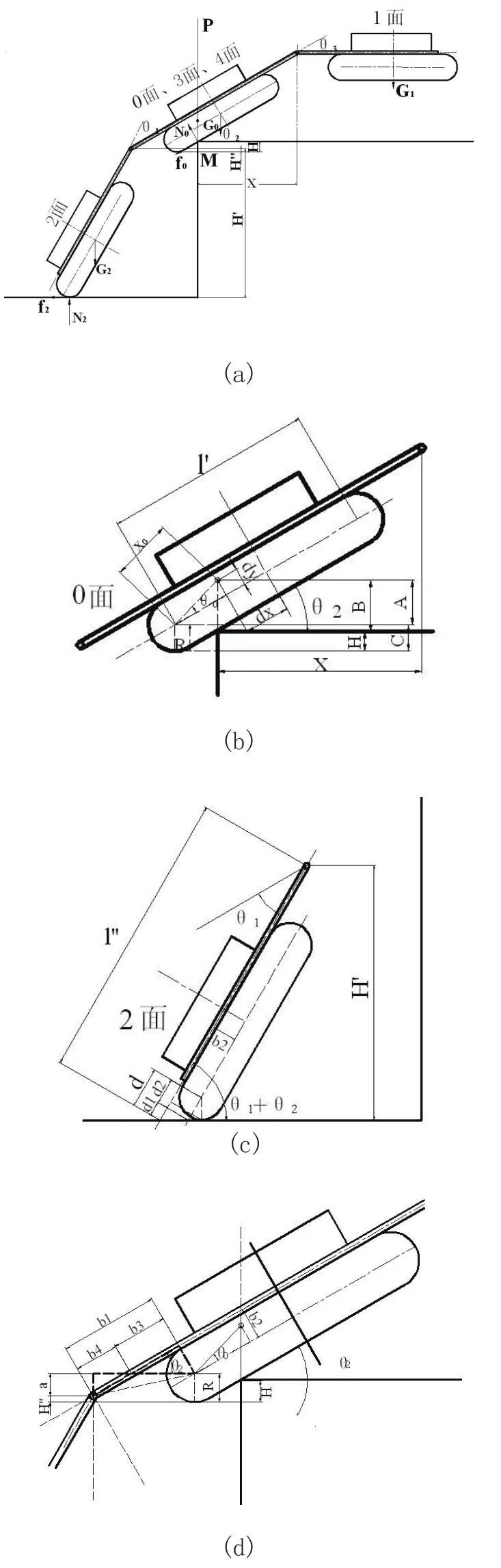
图5 机器人翻越台阶的姿态和受力图

由图5(a)和式(1)可知，X越小，也就是机器人的整体重心越靠近攀爬面1，越有利于翻越台阶。当机器人的驱动力足够大时，面0与台阶面所成的角度θ2取决于台阶与履带之间的摩擦系数。当θ2一定时，考察面2和面1的姿态对其翻越台阶能力的影响：由式(1)可知，若面1与面0的所夹角度θ3与面0与台阶面的接触角度θ2相等，即面1与台阶面平行时，机器人的整体重心最靠近攀爬端，机器人最容易翻越台阶；在此过程中，面2主要起抬起和支撑作用；面2与支撑面所成角度θ1+θ2≤90°时，面2与面0所成的角度θ1越大，面2与支撑面所成角度θ1+θ2越大，面0和面1被撑起的高度越高，越有利于机器人翻越台阶。

考虑机器人整体重心与X的关系，由图5(b)的几何关系可得：

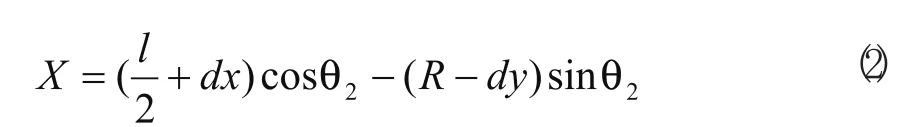
式中dx为机器人的整体重心沿前进方向的偏移；dy为机器人的整体重心沿垂直于前进方向的偏移；R为履带轮的半径。

由式(2)可知，机器人重心的位置直接影响机器人翻越台阶的能力，机器人的整体重心位置越低，即dy越小，其整体重心的位置越靠近攀爬端；dx越小，机器人的翻越台阶能力越强。

由上述的分析可知，在机器人的驱动能力相同的情况下，机器人的越障能力与机器人的重量，整体重心的位置，各面的相对姿态以及机器人履带与接触面之间的摩擦系数有关，调整机器人各个面之间的相对姿态，适当匹配相关参数，可以调整机器人整体重心的位置，获得最大的越障高度。由图5(a)的几何关系可得机器人的越障高度为：

式中H、H'、H''如图5所示。

其中，H由面0的几何关系如图5(b)可得：

式中ι'为同侧履带前后两履带轮的中心距。H'由面2的几何关系图5(c)确定：

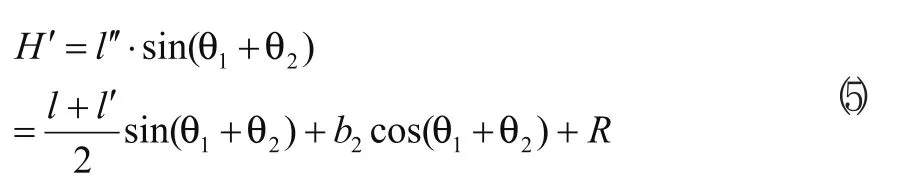
H''由面0的几何关系图5(d)可求得：

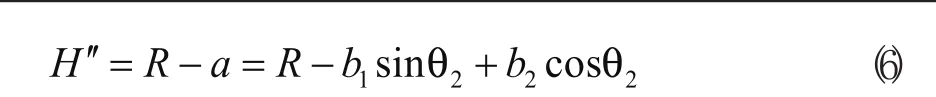
式中b1为面0上最左侧履带轮的中心到与面2相连接一侧的面0的边的距离，b2为履带轮中心到相应面板中心面的距离。

机器人翻越障碍物的过程中，面0与台阶面的夹角θ2∈(0°,90°)。

将式(4)、(5)、(6)代入式(3)化简得：

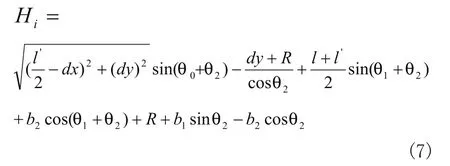
式(7)分别对θ1、θ2求偏导可得到

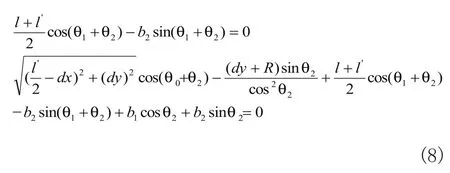
即当机器人面0与台阶面所夹角度θ2一定时，机器人的越障能力与θ1，θ2之和有关，调整面2与面0所成角度θ1使其满足式(8)时，机器人可获得最大越障高度Himax；当θ1一定，且0＜θ2＜90°时，随着θ2的增大，越障高度Hi增大。但考虑到实际情况，θ2的最大值受限于机器人的驱动能力，台阶面与机器人履带之间的摩擦系数，翻越台阶的回旋空间大小等参数，综合考虑上述因素可以求得机器人的最大越障高度Himax。

当机器人姿态一定时，翻越台阶的高度与机器人整体重心位置(dx,dy)有关，适当调整机器人各面的硬件分布，可以使其整体重心位置靠近攀爬端，提高其翻越障碍的能力。

2.2 爬楼梯能力分析

机器人爬楼梯时的情况与翻越台阶情况不同。机器人在爬楼梯时，由于回旋空间有限，其越障能力受到一定的限制。公共建筑或者住宅建筑内楼梯的坡度一般在20～38度之间，而且每节楼梯的宽度LT和高度HT通常是固定的。根据不同的情况，机器人爬楼梯的策略也不同，可以采用直接爬越方式或者变换姿态爬越方式。

当机器人的驱动力足够大，且机器人的尺寸满足一定条件时，才能采用直接爬越的方式，即机器人展开为扁平状，面0，1，2，3，4在同一平面内，并一直保持此姿态爬越，如图6所示。为了确保机器人直接爬越时的稳定性，爬越过程中机器人应满足前后至少有两个面和楼梯同时接触。考虑其临界状态：面1将要离开台阶时，面2刚好搭上台阶，由图6所示的几何关系可得直接爬越方式中机器人的尺寸ι'，履带轮中心距ι'和楼梯尺寸应满足式(9)关系：

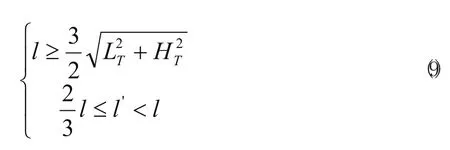
式中LT为楼梯的踏步宽度，HT为楼梯的踏步高度。

按照公共设施的楼梯尺寸LT=300mm，HT=150mm计算，由(9)式可得，当机器人尺寸ι≥503mm，履带轮中心距离ι'≥503mm时，才能采用直接爬越方式。若机器人的参数不满足式(9)时，机器人需要在爬越过程中变换姿态才能爬越楼梯。

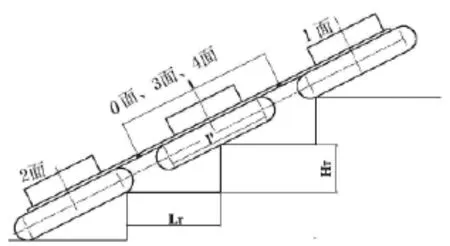
图6 机器人直接爬越楼梯图

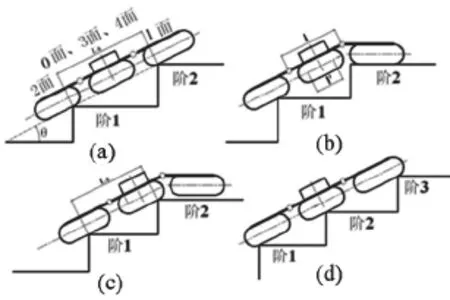
图7 机器人变换姿态爬越楼梯图

机器人采用变换姿态爬越楼梯方式如图7所示，在临界状态如图7(a)所示时，为了保证同时有两个面与楼梯接触，面1转动，使其与楼梯面接触，对机器人起牵拉的作用，如图7(b)所示；在面1和2的驱动下，面0，3，4搭上台阶2，如图7(c)所示；然后在面0和面2驱动下，面1伸展前爬，搭上台阶3，如图7(d)所示。在图7所示的爬越过程中，通过调整面1的姿态可以确保机器人稳定地爬越楼梯。此时，机器人参数需满足式(10)：

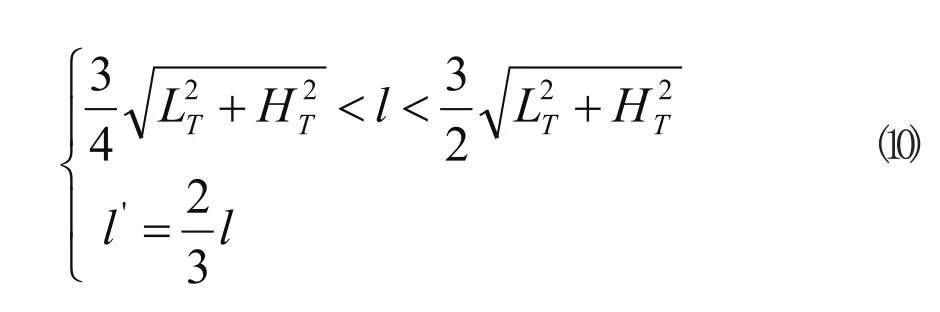
当机器人的尺寸更小，不满足式(9)、式(10)时，需要变换机器人面2，面1的姿态，实现稳定的爬楼梯动作。当机器人的尺寸足够小，使机器人在楼梯的台阶宽度上有足够的回旋空间时，可以采用第2.1节所述翻越台阶的策略爬越楼梯。

3 越障实验

根据以上的分析，对形状可变救助型机器人进行了翻越台阶和爬楼梯的实验。救助型机器人的实物如图8所示[3]。机器人的参数如表1所示。

图8 救助型机器人

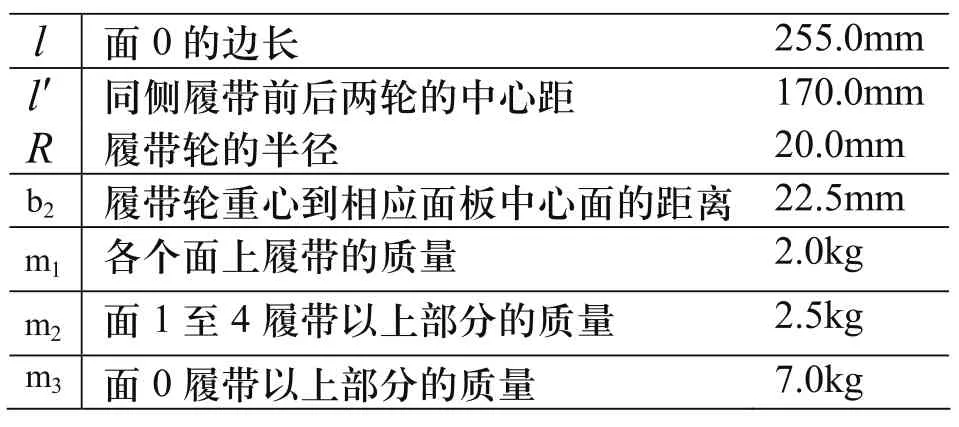
表1 救助型机器人的各结构参数

当台阶面为水泥面，履带的材料为橡胶时，根据实验可知机器人翻越台阶的最大高度为262mm，爬越过程如图9所示。考虑到实际机器人的结构，面0与面1，2之间的角度限制θ1，θ3小于45°，根据式(7)，式(8)，可求得机器人翻越台阶最大高度为260.5mm。与理论计算值比较，实际翻越高度略大。因为在实验过程中，略调整了面3和面4的位置，使机器人的重心高度发生变化，进而使其越障能力有所提高。爬越楼梯的实验如图10所示，木质楼梯LT=300mm，HT=150mm，此时主要通过调整面1的姿态，实现稳定地爬越楼梯。

图9 机器人翻越台阶

图10 机器人爬越楼梯

4 结论

本文提出了一种形状可变/多方位驱动救助型机器人的结构，分析了该机器人翻越台阶、楼梯典型障碍的运动过程及其最大越障能力，提出了不同障碍下的越障策略。得出如下结论：

1）形状可变救助型机器人翻越障碍过程中，通过变换机器人各面的姿态，可以使其各面分别发挥支撑，攀爬等不同的作用，最大限度地发挥其越障能力。

2）越障过程中形状可变救助型机器人的重心位置对其越障能力有很大的影响。合理安排机器人硬件的安装布局，改变机器人各面的姿态，变换机器人的形状，可以动态地调整机器人越障过程中的整体重心，提高机器人的越障能力。

3）爬越楼梯时，由于机器人的回旋空间有限，机器人的越障能力受到限制。根据机器人的几何尺寸，确立合适的爬越策略，可使其越障能力得到充分的发挥，实现稳定地爬越楼梯动作。

[1] 刘金国,王越超,李斌,等.灾难救援机器人研究现状、关键性能及展望[J].机械工程学报,2006,42(12):1-12.

[2] 李允旺,葛世荣,朱华,等.四履带双摆臂机器人越障机理及越障能力[J].机器人,2010,32(2):157-165.

[3] 段星光,黄强,李京涛.具有越障功能的小型地面移动机器人[J].机械设计,2006,23(4):38-41.

[4] Liu J G,Wang Y C,Ma S G,et al.Analysis of Stairs-Climbing Ability for a Tracked Reconfigurable Modular Robot.Proceeding of the IEEE International Workshop on Safety,Security and Rescue Robotics,2005,pp36-41.

[5] 余晓鑫,王孝洪,田联房,等.基于PC104单板微机和FPGA的救援救助机器人运动控制系统设计[J].制造业自动化,2009,31(9):95-97.

[6] 余晓鑫.形状可变/多方位驱动救援机器人控制系统设计[D].广州:华南理工大学,2010.

[7] 张勤,曲宁玺,王曼莉.一种形状可变/多方位驱动救助型机器人的结构[P].中国:实用新型专利,ZL200920215031.3.

[8] Tabata K,Inaba A, Zhang Q,et al.Development of a Transformational Mobile Robot to Search Victim under Debris and Rubbles,Proc.of the IEEE/RSJ Int.Conference on Intelligent Robots and System(IROS2004),2004:46-51.