防护门结构模态分析
2011-07-09林家炜张并瑞
林家炜 张并瑞 石 磊
1 模型建立
根据某防护门设计尺寸,如图1所示,门宽为4.3 m,高为3.0 m,门板厚15 cm。采用TrueGrid软件建立有限元模型,该模型共有1 653 316个节点,1 499 036个单元,其中包含19 286个梁单元。

图1 防护门结构示意图与透视图
结构的固有频率和振型确定是进行等效静载分析的基础,也是编制结构荷载实用计算方法的前提。通过使用分块位移求逆Lanczos方法对防护门进行模态分析,并研究防护门配筋对模态的影响。
2 模态分析的定义
模态分析是为了确定结构的振动特性,即结构的固有频率与振型,它们是结构受动态载荷作用时的重要设计参数,并且也是其他动力学分析问题的基础,如简谐响应分析和谱分析、瞬态动力学分析。模态分析是进行这些动力学分析所必需的前期分析过程。
LS-DYNA解法中的分块位移求逆兰乔斯法,它来源于波音公司的数据库(简称BCSLIB-EXT)。该解法采用共享内存的方法,它需求较大的内存,但计算速度快,并且能够精确的提取大模型的多阶模态(40阶以上)。

其中,K,M分别为组合刚度与质量;Φ,Λ分别为固有振型的特征向量与特征值。
Lanczos运算法则通过迭代计算,得出的特征值和与之相对应的特征向量值越来越接近真实值。

其中,A为一实对称矩阵,用于与特征向量相乘。当应用Lanczos运算法则计算振型分析问题时,式(2)应更改为:
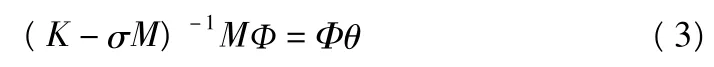
式(3)中每个分块求逆特征值为θi=1/(λi-σ)。经过更改后能够将复杂的问题转变为普通特征值问题,这将大大提高兰乔斯运算法则的计算速度。
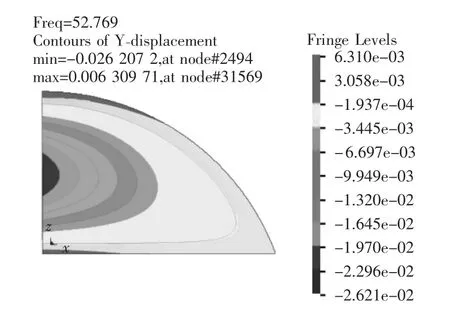
图2 第1阶振型图

图3 第2阶振型图

图4 第3阶振型图
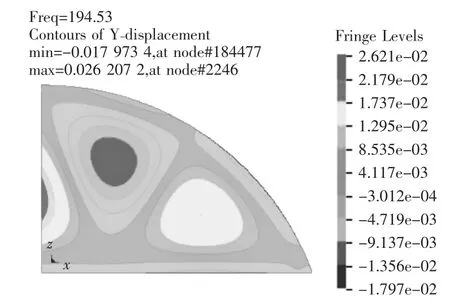
图5 第4阶振型图
Lanczos法通过精密的推导,选择一连串的转换值σi,使其能够计算大量的特征值与特征向量。在每次转变过程中,因式分解K-σM都得重新计算一遍。该因式分解提供的质量惯性矩阵能够说明在兰乔斯运算法则中需要多少个特征值再乘以给定的转换值σi。给定了惯性矩阵信息后,兰乔斯法能求出在一给定的求逆过程中有多少个特征值,并判断是否所有的特征值都已经过计算。因此,分块求逆兰乔斯法是个非常强大的解法。
3 防护门模态分析
使用*CONTROL_IMPLICIT_EIGENVALUE关键字对不同配筋情况下及素混凝土门板进行模态分析,并提取其20阶模态。图2~图5为配Φ16钢筋时防护门结构的第1阶~第4阶振型图。从图2~图5中我们可以清晰看出各阶振型的分布特征。
表1分别为配筋Φ16门板前10阶振型数据统计表。

表1 配Φ16钢筋时各阶振型数据统计表
另外通过计算得出了不同配筋情况下其1阶振型的数据,它们的固有频率素混凝土门板最小的为52.18 Hz,配Φ16钢筋的防护门为52.77 Hz,配 Φ18 的为 52.98 Hz,配 Φ20 的为 53.47 Hz。可见随着配备钢筋率的提高,防护门固有频率逐渐增大,但变化幅度相对较小。
比较其余各阶振型的数据可以得出类似的结论。
4 结语
通过以上研究表明,利用LS-DYNA有限元软件对防护门进行模态分析是可行的,通过Lanczos法能够得出防护门结构各阶阵型的分布特征以及其特征值、频率等相关数据,从而为求得防护门结构的简化计算解析解奠定了基础。
[1] 战 颂,徐永君,张均锋.钢包砼拱形防护门有限元模态分析[J].地下空间与工程学报,2006(12):78-79.
[2] 陆新征,江见鲸.抗爆门结构考虑接触影响的动力有限元分析[J].力学与实践,2003(15):32-33.
[3] 11th International LS-DYNA users conference,2010.
[4] LS-DYNA Keyword User’s Manual Version 971/Release 4,2009:50-55.
[5] LS-DYNA Keyword User’s Manual Version 971/Release 5,2010:20-25.
[6] 齐春龙.门式刚架结构设计浅谈[J].山西建筑,2010,36(1):93-94.
