超高压输电杆塔结构体系可靠性研究
2011-07-09费继萍张学礼
费继萍 张学礼 秦 力
0 引言
超高压送电线路是重要的生命线电力工程设施,杆塔及基础投资约占线路总投资的30%,其结构安全可靠性意义重大。近几年我国500 kV输电线路倒塔事故呈上升趋势,给我国经济造成了巨大损失[1]。尤其是2008年1月的低温冰雪灾害使得我国大量电网输电线路杆塔倒塌、变形和存在隐患。因此对已建高压输电杆塔进行结构可靠性分析具有重要意义。
1 载荷增量最小准则法识别系统主要失效模式
载荷增量最小准则法是在优化准则法的基础上,通过考虑内力反向现象而改进的识别结构系统主要失效模式的方法[2]。
由 n 个单元组成的结构系统中,设 r1,r2,…,rk-1共(k -1)个单元已相继失效,它们对应的载荷增量因子分别是ΔF(r11),ΔF(r22),…,ΔF(rkk--11)。在失效历程第k阶段,通过式(1)计算单元 rk[rk∈(1,2,…,n),rk∉(r1,r2,…,rk-1)]的有效强度 R(rkk)和载荷增量比。

其中,RIrkrk为单元rk的考虑拉压差异的单元强度;ΔF(rkk)为在失效历程第k阶段对应于单元rk失效的外荷载增量因子;mri为材料选择参数,当失效单元ri由理想弹塑性材料组成时,mri=1;当失效单元ri由理想脆性材料组成时,mri=0;IA为算法选择参数。
给定分枝—约界参数ck(1≤ck<∞),满足下式的单元rk在失效历程的第k阶段将成为失效候选单元。

由于ΔF(k)rk对应的是沿着失效路r1→r2→…→rk由失效历程的第(k-1)阶段演变到失效历程第k阶段的载荷增量因子,当rk取满足条件ΔF(k)min=min[ΔF(k)rk]所对应的单元时,系统的外荷载增量取值最小。显然,式(2)保证了在失效历程的任意阶段,总是使系统外荷载增量取值较小的那些单元进入主要失效模式。在失效历程第k阶段,沿失效路r1→r2→…→rk,系统所能承受的最大外载(以广义外载为一个计量单位)为:
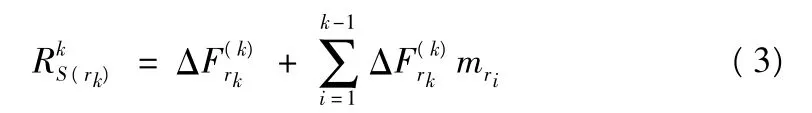
设r1,r2,…,rk共k个单元已相继失效,由系统失效判据知此时结构已失去继续承受所加外载的能力。根据增量加载理论,结构系统的加载过程可表示为:
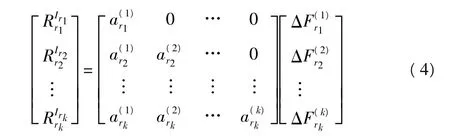
失效历程第k阶段的系统阶段临界强度(以广义承载为一个计量单位)为:
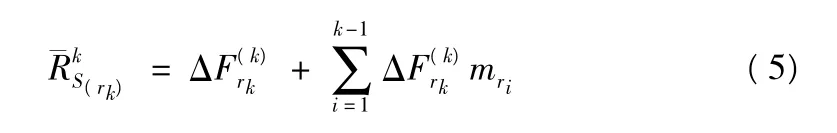
失效模式r1→r2→…→rk所对应的安全欲量方程为:

2 基于Matlab优化工具箱的可靠度计算
2.1 基本原理
假设X1,X2,…,Xn是n个独立随机变量,其分布函数为Fi(Xi)(i=1,2,…,n),由这 n个随机变量表示的结构功能函数为[3]:
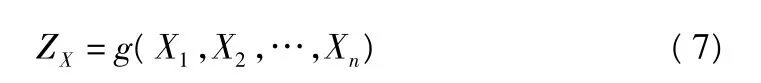
采用R—F(拉科维茨—菲斯来法)将非正态随机变量当量正态化:

其中,Φ为正态函数;Yi为相互独立的标准正态随机变量。
求分布函数Fi(Xi)的反函数为:

将式(9)代入式(7)得:

在标准正态坐标系中,由可靠度指标的几何意义是原点到极限状态曲面的最短距离可知:

开始时验算点未知,把β看成极限状态曲面上点P(Y1,Y2,…,Yn)的函数,通过优化求解找到β最小值,即可得到可靠度指标β和验算点P*(Y*1,Y*2,…,Y*n)。求解可靠度指标可以归结为以下约束优化模型[3]:
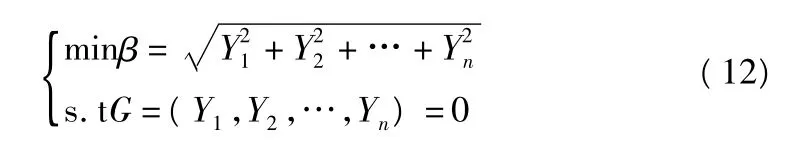
2.2 程序开发
Matlab主要源程序:
function relia% 定义主函数
y0=[0,0,0];%初始迭代点,这里取均值%调用优化工具箱
options=optimset('LargeScale','off');
[Y,fval]=fmincon(@objfun,y0,[],[],[],[],[],[],@stfun,options);
Pf=cdf('norm',- fval,0,1);
fprintf('可靠度指标为 β=%f ',fval);
fprintf('标准正态空间中验算点为 [%f,%f,%f] ',Y(1),Y(2),Y(3));
fprintf('失效概率为 Pf=%f ',Pf);
function f=objfun(y)%目标函数子函数
f=sqrt(y(1).^2+y(2).^2+y(3).^2);%即为 β
function[c,ceq]=stfun(y)%约束条件子函数
c=[];
ceq=(2.0212+0.2425.*y(3)) - (0.1929+0.0135.*y(2)) -0.9144+log( - log(normcdf(y(1),0,1)))./6.7454。
3 算例分析
对某500 kV线路,按30 m/s计算基准风压,导线平均高度取30 m~45 m,导线选用4×300~4×500,水平挡距取300 m~800 m,垂直挡距取水平挡距的1.2倍~1.5倍。塔身主材主要采用Q345L125×10,Q345L125×8,Q345L110×8。按文献[4],计算得导地线线条风荷载与自重荷载比值A=0.6~1.3。根据500 kV线路杆塔的统计资料,杆塔自重与导地线自重比值B=0.5~2;塔身风合力与导地线线条风荷载比值C=0.5~1;导地线合力作用点高度与铁塔根开比值D=3~5[4]。为了便于计算和比较,取A=1,B=1,C=0.75,D=4,取安全系数 K=1.5,SQK=1。
应用载荷增量最小准则法求解此输电杆塔的主要失效模式。在失效历程第1阶段,计算各个单元的内力,单元208载荷增量值最小,假定单元208先失效,计算过程见表1。
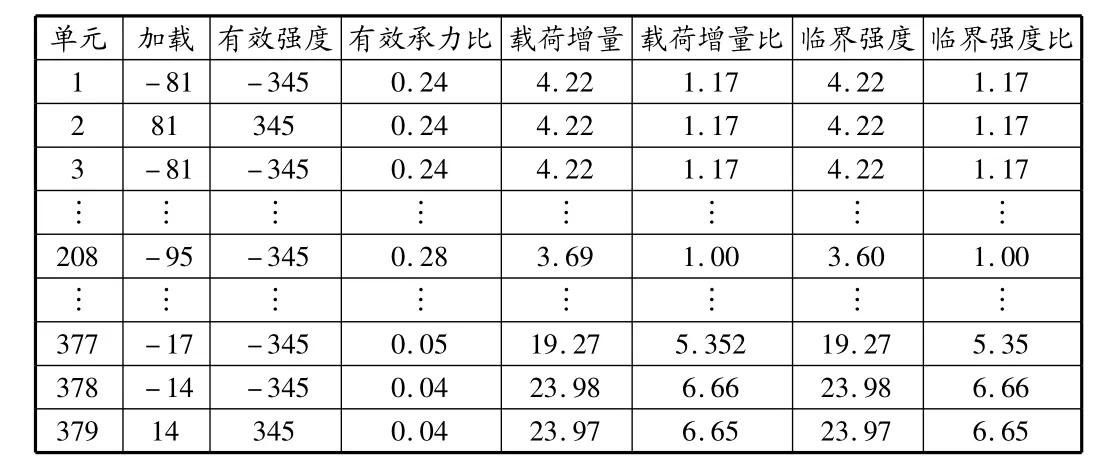
表1 失效历程第1阶段应力分析结果
给定分枝—约界参数c1=1.5,满足5.403 1的单元r1在失效历程的第1阶段将成为失效候选单元,可见:
杆208失效后,结构还未形成机构,还需继续操作,删除失效单元208,通过外加虚荷载,实现结构状态的转移,并由此进入失效历程第2阶段。失效历程第2阶段计算过程举例见表2。

表2 失效历程第2阶段应力分析结果
给定分枝—约界参数c2=1.5,满足ΔF(2)r2≤c2min[ΔF(2)r2]=5.430 6的单元r2在失效历程的第2阶段将成为失效候选单元,可见:

杆208,200失效后,结构还未形成机构,还需继续操作,删除失效单元208,200,通过外加虚荷载,实现结构状态的转移,并由此进入失效历程第3阶段。
给定分枝—约界参数c3=1.5,满足ΔF(3)r3≤c3min[ΔF(3)r3]=1.5的单元r3在失效历程的第3阶段将成为失效候选单元,可见:

杆208,200,169失效后,结构还未形成机构,还需继续操作,删除失效单元208,200,169,通过外加虚荷载,实现结构状态的转移,并由此进入失效历程第4阶段。
用同样的操作继续对其他未失效的单元进行操作,我们找到了19个主要的失效路径,每个失效路径都是由4个失效单元组成,这些主要的失效路径即为此500 kV输电杆塔结构的主要失效模式,见表3。

表3 根据主要失效模式集计算的系统综合失效概率
利用基于Matlab优化工具箱的可靠度计算方法,考虑上面19个主要失效模式,并且各个失效模式之间的相关系数为1。编制可靠度和相应失效概率的程序,分别计算各个失效模式的失效概率和体系的综合失效概率,计算结果见表3。
4 结语
通过分析某500 kV猫头型输电杆塔的结构体系可靠性,可以看出其主要失效模式的平均可靠度¯β=2.356 2,系统失效概率的区间为[2.562 9 ×10-2,2.927 3 ×10-2]。而 GB 50068-2002 建筑结构可靠度设计统一标准的标准规定[5]:一般的建筑结构安全等级为二级,其延性构件的目标可靠指标为3.3。而且本文计算时仅考虑结构的构件强度条件、风荷载和恒载的组合,对于送电杆塔结构的构件设计还需考虑构造要求和其他可变荷载同时参与的组合。因此,我国超高压输电杆塔结构体系的可靠度有待进一步提高。
[1] 唐国安.我国500 kV线路倒塔事故率浅析[J].电力建设,1994,15(11):18-20.
[2] Feng Y S.Enumerating Significant Failure Modes of A Structural System by Using Criterion Methods[J].Compt.& Struct,1988,30(5):1153-1157.
[3] 李志华,张光海,康海贵.基于Matlab优化工具箱的工程可靠度计算[J].四川建筑科学研究,2005,31(3):1-4.
[4] 陈海波,廖总高,肖洪伟.受风荷载控制的杆塔结构体系可靠度分析[J].电力建设,2007,28(7):40-45.
[5] GB 50068-2002,建筑结构可靠度设计统一标准[S].
