基于试验的承重保温砌块本构关系

刘凌翔,谢献忠,刘锡军

(湖南科技大学土木工程施工过程与质量安全控制湖南省普通高校重点实验室,湘潭411201)

0 引 言

承重自保温结构是我国近几年提出的一种新型保温节能结构形式,该结构墙体由蒸压加气混凝土砌块和配制的轻质砌筑砂浆砌筑而成.蒸压加气混凝土砌块的干表观密度一般为325～825 kg/m3,抗压强度为3～6 MPa,导热系数为0.10～0.20 W/(m◦K)[1].由于保温砌块和普通烧结或混凝土砌块的基本力学性能差别较大,砌块在砌体中的受力状态和破坏机理也有所不同,研究保温砌块的本构关系对保温砌体数值分析具有极为重要的意义.根据文献[2]所述,不同砌块尺寸和不同约束条件下所获得的应力-应变关系并不相同,为了模拟砌体中砌块的实际受力特征,本试验采用电液伺服试验机对5个保温砌块进行受压试验,模拟砌块在砌体中相近的受力条件,获得相应的本构关系,为保温砌体有限元分析提供基本力学参数.

1 试验方案及结果

(1)试件尺寸

图1 砌块加载装置

保温砌体中保温砌块的变形模量低于轻质砂浆的变形模量,砂浆对砌块具有一定的约束效应,本试验采用5块湘潭发电厂粉煤灰制作的规格为A5.0、尺寸为240 mm×115 mm×90 mm的保温砌块,在加载板接触面的摩擦力作用下产生的侧向约束远大于一般单轴受压试验的约束效应,故此试验方法获得的全应力-应变曲线可模拟保温砌块在砌体中的约束效应,加载方式如图1所示.

(2)加载设备及数据采集

试验采用微机控制电液伺服试验机WAW-600L的压缩功能进行加载,在受压应力-应变全曲线测试过程中,不需要另外增加刚性元件,试验根据预先设定的加载程序进行自动控制和数据采集.

(3)试验结果

根据试验机采集的数据经整理得到保温砌块实测应力-应变全曲线和归一化处理后的应力-应变全曲线如图2、图3所示.

2 数据分析

(1)屈服应力σy和屈服应变εy的确定

由于试验数据的离散性,根据几何作图法确定σy和εy,其方法如图4所示.

几何作图法,作直线OA与曲线初始段相切,与过σo的水平线相交于A点,作垂线AB与曲线交于

图4 初始屈服点的确定

B点,连OB并延伸交于C点,作垂线的Y点,及相应的屈服应力和应变.根据实测应力-应变数据分析,当初始应力很小时,由于构件接触面不密实,造成位移过大的假象,不能作为确定初始切线的依据,数据处理中采用0.15倍σo应力与0.3倍σo应力和相应的应变作为初始切线斜率计算依据.

(2)极限应力σμ和极限应变εμ的确定

确定极限点应力 σμ可以取最大承载力下降15%所对应的应力值,即 σu=0.85σ0和相对应的应变 εμ[3].

(3)试验数据离散性分析

为了检验试验数据的离散性是否符合一般统计规律,对所测得的应力-应变曲线特征点数据进行统计分析,其具体分析数据见表1所示.

表1 保温试块试验数据离散性分析表

根据以上数据分析,所有特征点参数的最大变异系数为0.161,小于0.2达到一般试验水平,其中屈服应变的变异系数为0.098,表明弹性阶段试验数据离散性较小(因数据量较少,此变异系数并不能代表该参数的离散性),所测数据可作为参数分析的依据.

3 受压本构方程

以试验数据为基础,根据文献[4]建议的受压应力-应变全曲线理论方程为:

为了和标准公式统一,对试验平均值进行归一化处理,其结果如表2.

表2 特征点归一化分析表

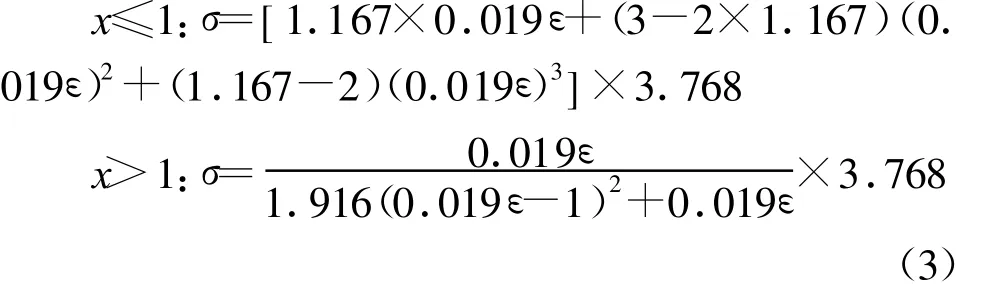
保温砌块本构关系理论曲线及与试验结果对比分析如图5、图6所示.

4 结 语

(1)通过模拟约束保温砌块的受压试验所得的应力-应变全曲线,其试验结果离散性较小,可作为保温砌块本构方程的依据;

(2)通过对试验数据分析和处理,获得保温砌块本构方程与试验结果吻合较好;

(3)基于试验结果的保温砌块受压本构方程能模拟砌块实际受力及变形特征,可作为保温砌体数值模拟的基本参数.

[1]全国水泥制品标准化技术委员会.GB11968-2006蒸压加气混凝土砌块[S].北京:中国标准出版社,2006:2-3.

[2]Hemant B.Kaushik,Durgesh C.Rai,Sudhir K.Jain,M.ASCE.Stress-Strain Characteristics of Clay Brick Masonry under Uniaxial Compression[J].JOURNAL OF MATERIALS IN CIVIL ENGINEERING ASCE/SEPTEMBER,2007:728-739.

[3]过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2009.

[4]过镇海,张秀琴.单调荷载下的混凝土应力-应变全曲线试验研究[M].北京:清华大学出版社,1981.

[5]过镇海,张秀琴,等.混凝土应力-应变全曲线的试验研究[J].建筑结构学报,1982,(3):1-12.