变频调速异步电机的谐波分析
2011-07-09刘万太谢卫才李永坚
刘万太,彭 晓,谢卫才,李永坚
(1.湖南工业大学电气信息工程学院,株洲412008;2.湖南工程学院电气信息学院,湘潭411101)
近些年来,变频电机的应用越来越广泛.用于变频调速的异步电机采用变频器供电,与电网供电不同,变频电源的输出电压和电流中含有大量的高次谐波,这些谐波会对异步电机的运行性能产生较大的影响,所以对变频电机的谐波分析就显得尤为重要.
变频调速异步电机气隙磁场的分布受多种因素的影响,从谐波产生的原因来看,可分为空间谐波和时间谐波.空间谐波是由电机的本身结构决定的,电机定子绕组的分布、定转子开槽、铁心饱和等原因都会导致空间谐波的产生.另外,由于电力电子技术的迅速发展,电力半导体器件广泛应用于变频器装置中.当采用变频器供电时,变频器内的半导体处于重复的开关暂态,导致输出并不是理想的正弦波,还含有大量的高次谐波,这就是时间谐波的来源.可见,变频器的使用使异步电机的谐波分析问题更加复杂.
本文主要针对谐波的产生基理、对电机运行特性的影响等方面做了分析,并运用MATLAB进行了仿真.
1 变频调速异步电机的谐波分析
变频调速异步电机气隙磁场的分布受多种因素的影响,从谐波产生的原因来看,主要可分为时间谐波和空间谐波.
1.1 变频电机气隙磁场中的时间谐波
变频电源的输出波形相当于重复的开关暂态,而不是标准正弦波形,因此包含有大量的高次谐波.假设异步电机的三相绕组对称,则在非正弦电源驱动下会产生三相对称的非正弦电流,该电流按傅立叶分解如下:
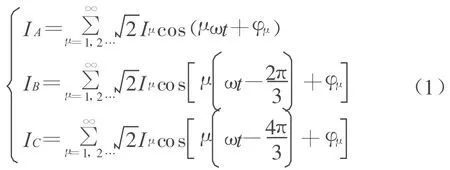
其中,Iμ为μ次谐波电流的有效值,φμ为 μ次谐波电流的初相角.
谐波电流会在电机中建立基波磁场和一些列谐波磁场.例如谐波中的5次谐波分量对于每一相建立一个与基波有同样空间分布的磁势驻波,以5倍于基波脉动,则5次谐波电流产生的基波磁势为:
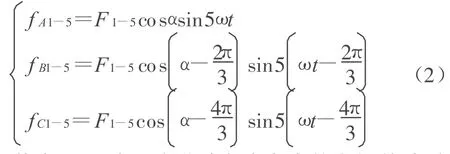
其中,F1-5为5次谐波电流产生的空间基波磁势最大值,α为坐标原点选在绕组轴线上时,沿定子内圆表面的电位移角.
三个磁势相加得到合成磁势为:
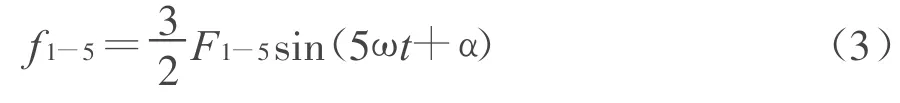
上式说明5次谐波电流产生一个旋转磁势,旋转速度为dα/d t=-5ω这就意味着这个磁势波以5倍与同步转速沿着与基波磁势相反的方向移动.
同样可以证明,7次谐波电流产生一个7倍于同步转速而方向与基波方向相同的旋转磁势.通常谐波次数k=3n+1的电流产生正向旋转磁势波,k=3n+2的电流产生反向旋转磁势波(这里n=0,1,2…).
1.2 变频电机气隙磁场中的空间谐波
这里先从分析一个线圈的磁势着手,然后再通过叠加合成得到电枢绕组的三相磁势.
在标准正弦电源供电的情况下,假设线圈里流过的是标准正弦交流电i,则可以得到:


该磁势的幅值大小随时间按余弦规律变化,是一个脉振波,在空间的分布是一个矩形波.
相绕组的磁势是有单个线圈绕组磁势叠加而成,然后再把单相磁势合成为三相磁势.对于空间基波,A、B、C三相电流相位互差 120°,同时在空间分布上也互差120°,可以得到三相合成后的基波脉振磁势为:
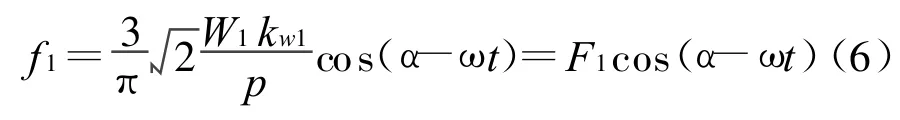
式中F1是三相基波磁势的幅值.
当异步电机采用变频器供电时,需要考虑电源输入的电流时间谐波,此时,三相基波气隙磁势的表达式为:

通过对上述基波磁势和谐波磁势表达式的分析,不难得出空间磁势的通用表达式如下:
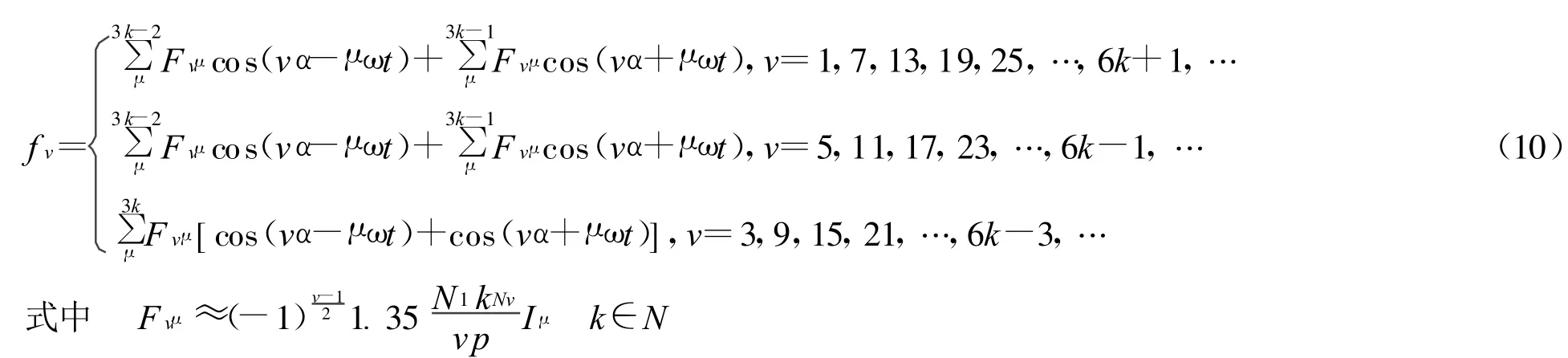
从上式不难看出,谐波电流产生的空间旋转磁势的幅值与绕组系数和谐波电流的幅值成正比,与空间谐波次数成反比.
2 谐波对变频电机的影响
在变频调速系统中,采用电力电子变压变频器作为驱动电源,供电系统中不可避免地存在大量的高次谐波成分,对外表现为非正弦供电.
这些高次谐波对电机的影响主要表现为磁路中的谐波磁势和电路中的谐波电流.谐波电流导致的谐波损耗主要可分为定、转子绕组谐波电流产生的附加铜损耗,电源谐波产生的附加铁耗和附加杂散损耗等.这些损耗会导致电机的效率和功率因数降低、电流升高、温升增加等一系列问题.一台普通异步电机在变频电源驱动下,其温升比标准正弦电源驱动要增加10%~20%.同时这些谐波磁动势与转子谐波电流合成又产生恒定的谐波电磁转矩和振动的谐波电磁转矩,这些振动的谐波电磁转矩会使电机产生脉动,从而造成电机转速(主要是低速时)振荡,甚至引起系统不稳定.谐波电流还导致电机峰值电流增大,在一定的换流能力下,谐波电流降低了逆变器的负载能力.
此外,电力电子变频器运行时产生的副作用还有:传导和辐射的电磁干扰、对电机的绝缘结构破坏严重、振动和噪声增大等一系列问题.对于变频电机,要在设计过程中综合考虑这些影响,采取合理的措施避免或减小变频器供电对异步电机造成的这些影响,以达到最佳的技术效果.
3 变频器驱动下异步电机的仿真分析
3.1 异步电动机的数学模型
要建立准确的数学模型,首先要做如下假设:①电机气隙均匀且不计磁路饱和的影响;②异步电机的各相绕组完全对称;③磁路是线性的,气隙磁场沿圆周按正弦规律分布;④不考虑频率和温度变化对绕组电阻的影响.
为了使仿真模型能够正确建立,往往需要将A、B、C三相静止坐标系转换到相对比较简单的两相坐标系下,以达到解耦的目的.本文中将A、B、C三相坐标转换成静止的α、β两相坐标系.因为三相异步电动机的转子电压 uαr=uβr=0,可以得到以定子磁链和定子电流为状态变量的状态方程如下:
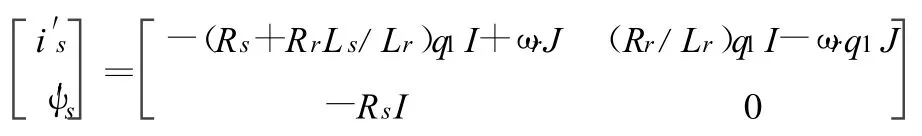

Rr、Lr为转子电阻与电感;为激磁电抗;
为方便建模将式(11)进一步展开,可得下式:
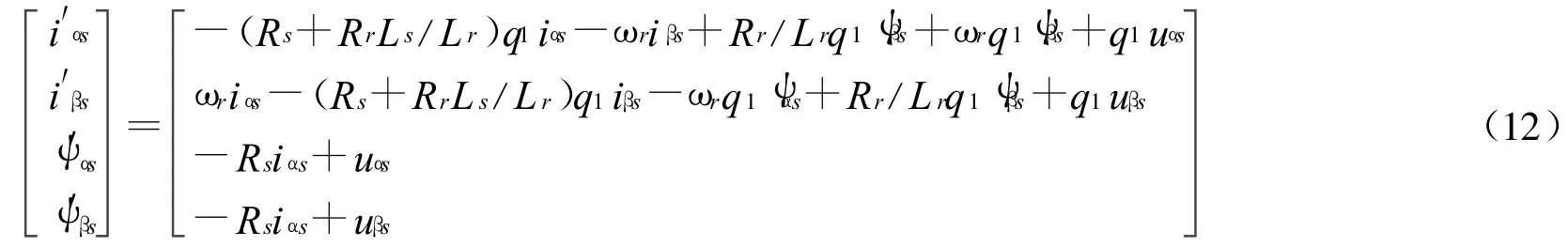
电机的电磁转矩方程:
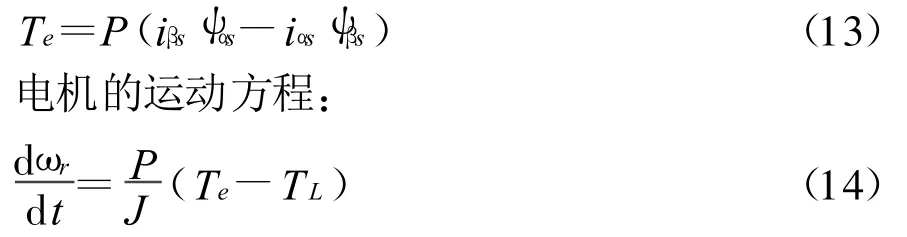
式中Te、Tl分别为电磁转矩和负载转矩;
J为转动惯量;P为基波极对数;
3.2 变频调速异步电机的系统仿真模型
根据上述分析得到的数学模型在Simulink中先分别建立3s/2s模块和DEE模块,然后组成如下图1所示的系统仿真模型.
采用上述变频调速系统的仿真模型,分别在标准正弦供电时和变频器供电时对一台普通异步电机进行仿真,得到的转矩和电流波形如图2所示.
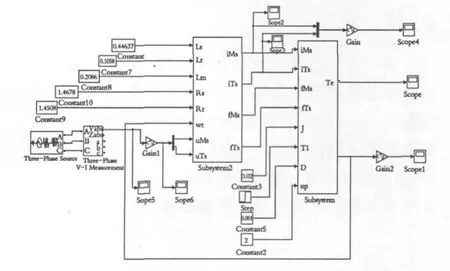
图1 变频调速异步电机系统仿真模型
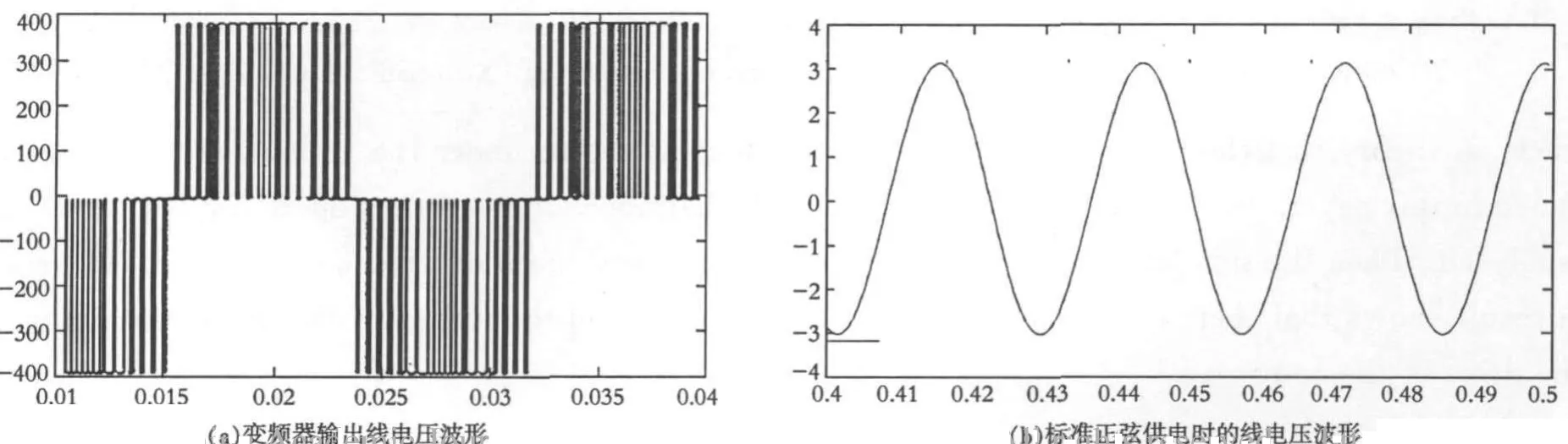
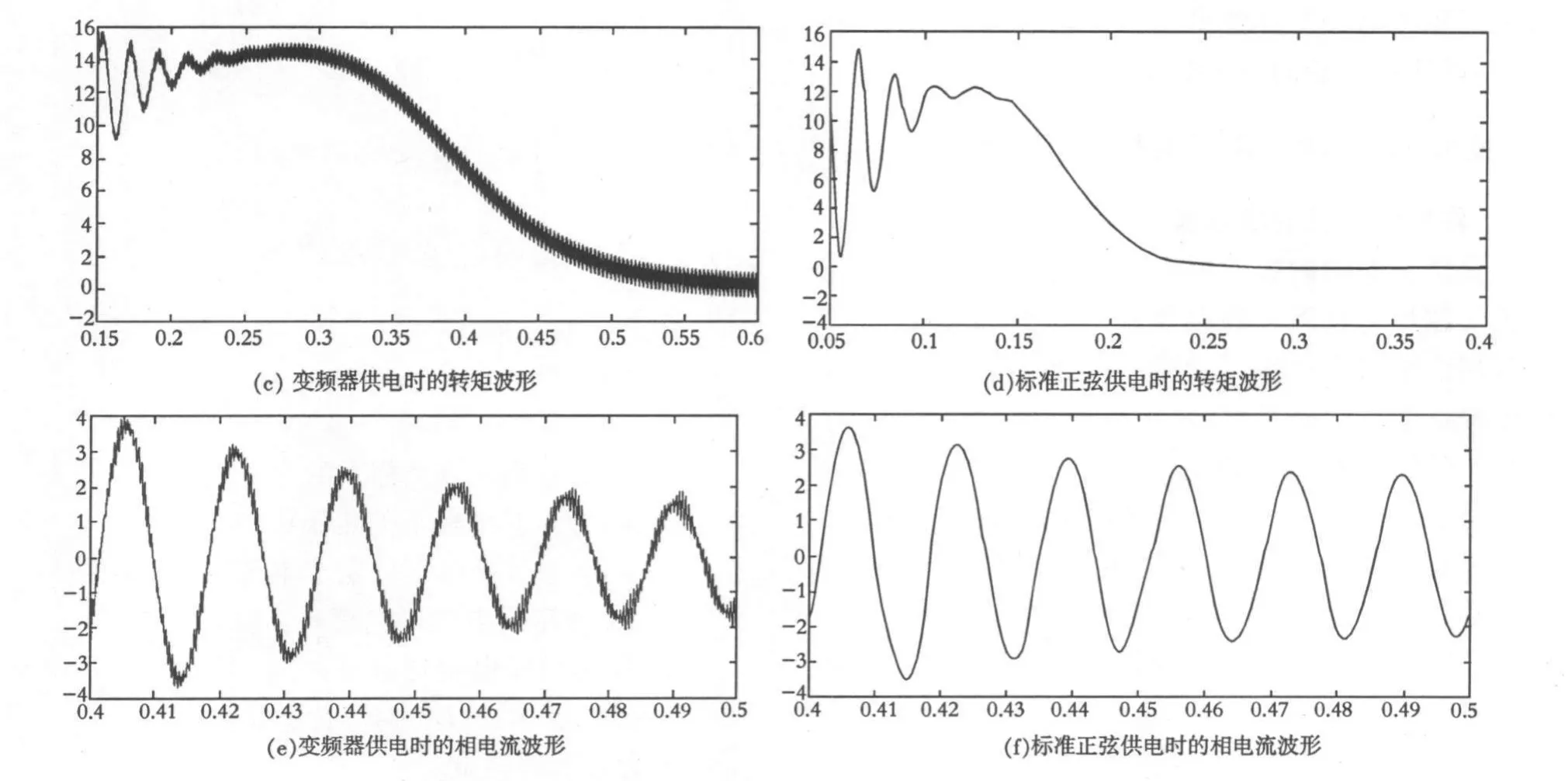
图2 异步电动机变频器供电与标准正弦供电仿真波形图
从仿真结果可以看出,变频器供电时,异步电机的输入电压为一系列宽度不等的脉冲电压,如果对该电压进行傅立叶分解,会发现除了含有基波外还含有大量谐波成分.这些谐波的存在使得异步电机的转矩和相电流出现较明显的脉动.
4 结 语
本文主要从理论分析入手,分析了异步电机在变频电源驱动下的谐波产生原理及对电机运行性能的影响.随后建立了变频调速系统的仿真模型,并对变频器供电及标准正弦供电时电机的性能进行了比较,仿真结果表明,变频电源驱动下的异步电机转矩波形及电流波形都出现了明显的脉动.
[1]Boglietti A,LazzarM,PastorelliM.A Simplified Method for the Iron Losses Prediction in Soft Magnetic Materials with Arbitrary Voltage Supply[J].IEEE,2000:269-276.
[2]王凤翔.交流电机的非正弦供电[M].北京:机械工业出版社,1997.
[3]上海电器科学研究所.中小型电机设计手册[M].机械工业出版社,1994.
[4]姚 俊.Simulink建模与仿真[M].西安电子科技大学出版社,2002.
[5]魏华雄.SPWM逆变供电下感应电机谐波分析及仿真[D].哈尔滨理工大学硕士论文,2004.
[6]吴安顺.最新实用交流调速系统[M].北京:机械工业出版社,1998.
