基于数学形态学的彩色图像边缘检测

王金凤， 焦斌亮

（燕山大学信息科学与工程学院，河北 秦皇岛 066004）

边缘是图像的一个基本特征，携带了图像中的大量信息。边缘检测不仅能得到关于边界的有用的结构信息，而且还能极大地减少要处理的数据，很多图像处理和识别算法都以边缘检测为重要基础。边缘按其颜色特征可分为灰度边缘和彩色边缘。长期以来，人们主要致力于灰度边缘的研究并取得了很好的效果，如经典的Canny算子和Sobel算子等。但彩色图像能够比灰度图像提供更多的信息。有研究表明[1]，彩色图像中，大约有90%的边缘与灰度图像中的边缘相同，也就是说，有10%的边缘在灰度图像中是检测不到的。因此，彩色图像的边缘检测越来越受到重视[2-3]。

数学形态学[4]是基于非线性理论的图像分析处理方法，是由G Matheron 和 Jean Serra于1964年提出，并广泛成功地运用于图像处理和模式识别中。最初的形态学是以二值图像为研究对象，称为二值形态学。Serra，Sternberg等将数学形态学推广到对灰度图像的处理，称为灰度形态学。把灰度形态学推广到彩色图像的研究已经积累了一定的成果，特别是 Serra, Goutsias 等人作出了突出贡献。

彩色图像是向量值函数，向量之间是不可比较的，因此，不能把灰度形态学直接推广到彩色图像。根据Goutsias的研究[5]，当确定了像素向量之间的排序关系后，就可以像定义灰度形态学一样定义彩色形态学的腐蚀、膨胀。利用这两个基本算子可以组合出更多的算法。Goutsias描述的彩色形态学定义仅给出了理论方法，具体实现需要根据表示图像的颜色空间设计颜色向量的排序方法。计算机系统和大多数捕获或显示图像的硬件设备都使用RGB颜色空间，对于HSI和Lab等颜色空间，必须先从 RGB颜色空间变换到该空间处理，再变换回RGB颜色空间输出，变换过程中容易丢失信息，计算繁琐，增加时间开销。在RGB颜色空间，尹星云等人将距离和字典序相结合，基于此向量序提出了彩色图像形态学基本算子[6]。但是这些算子和传统灰度算子一样对噪声敏感，抗噪性能差，无法直接通过梯度运算进行边缘检测，本文结合 Adrian N Evans[7-8]等人的思想，在RGB颜色空间，采用距离和字典序相结合的向量序，改进了彩色图像形态学膨胀腐蚀算子。该算子有很强的抗噪性，可以直接通过梯度运算进行边缘检测。

1 彩色图像形态学及算子改进

1.1 颜色向量序[6]

令 f =( fR, fG, fB)是RGB颜色空间的彩色

通过亮度计算方法的实验，给式(1)右端的fR, fG, fB分别乘上权值： wR= 0 .299，wG= 0 .587,wB= 0 .114，则任意一个像素点x到白点的加权距离为

1.2 彩色图像形态学基本算子

利用上述定义的彩色图像像素排序方法，就可以给出彩色图像形态学基本算子。令B表示结构元素， NB(x)表示像素点x的邻域x∈Ω , Ω ∈ z2是彩色图像 f的定义域，maxψ(⋅)表示按照关系ψ取最大值，minψ(⋅)表示按照关系ψ取最小值。

用B对f膨胀定义为

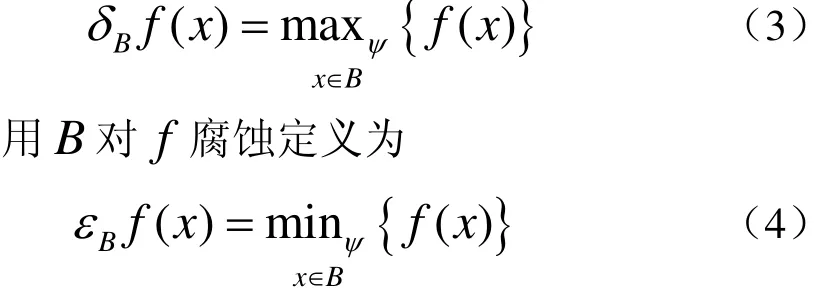
1.3 改进的彩色图像形态学基本算子

根据颜色向量序ψ定义的上述彩色图像形态学膨胀、腐蚀算子式(3)、式(4)，能够较好地对彩色图像进行膨胀和腐蚀处理，但是它们和经典的灰度形态学基本算子一样对噪声敏感。本文针对噪声（主要是椒盐噪声）污染彩色图像的特点，对上述算子进行了改进。

椒盐噪声（双极脉冲噪声）是图像处理中十分常见的一种噪声，它可以产生于图像捕捉设备传感器上的坏点或者强噪声信道条件下的图像传输过程。因为脉冲干扰通常比图像信号要大，所以噪声总是数字化为最大值。从某种意义上看，它们等于所允许的最大值或最小值。

上述maxψ(⋅)表示按照关系ψ取最大值，因为“胡椒”噪声是非常低的值，这样可以有效的消除“胡椒”噪声的影响，但无法去除“盐”噪声的影响。“盐”噪声是非常高的值，在窗口内求最大值的时候，“盐”噪声最有可能被作为最大值赋给图像。因此，本文提出一种简单而有效的方法，即通过找出窗口内的最大值，判断其是否为噪声点，如果是，移除求新的最大值，然后再次做判断，此过程反复进行，直到求得的最大值是可能的像素点。

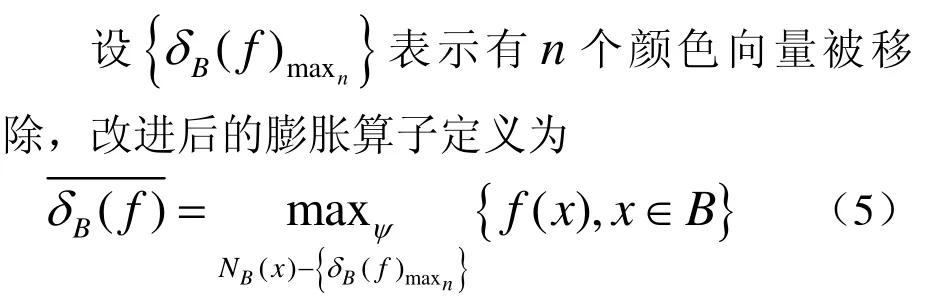
同理，改进的腐蚀算子每次计算的时候，计算出最小值，然后判断是否为噪声点，如果是就移除，然后再次判断，反复进行，直到求得的最小值是可能的像素点。

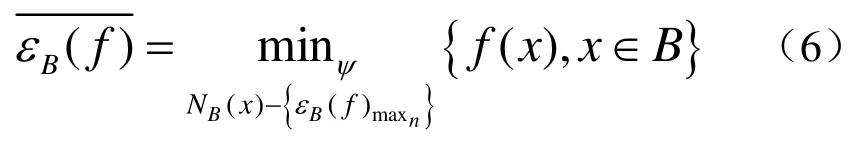
如图1所示，图1(a)为RGB空间的lena图像，图1(b)为加入10%椒盐噪声的lena图像，图1(c)和图 1(d)分别为对加噪后的图 1(b)进行膨胀和腐蚀处理的结果。

图1 改进的彩色图像形态学基本算子

结果表明图1(b)得到了膨胀、腐蚀（如立柱的粗细和lena瞳孔的大小都有改变，以及图1(c)中帽檐上方的黑色横线被膨胀掉了和图1(d)中帽檐上的白色横条被腐蚀掉了），同时噪声明显消除，说明该算子也有滤波作用，具有抗噪性。

1.4 基于改进形态学基本算子的边缘检测算法

利用前面提出的改进的彩色图像形态学算子，可以将下面这几种边缘检测算子用于彩色图像的边缘检测。

按照腐蚀操作构造图像边缘检测算子可表示为

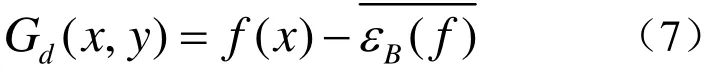
这样得到的是图像的内边缘。

按照膨胀操作构造图像边缘检测算子可表示为

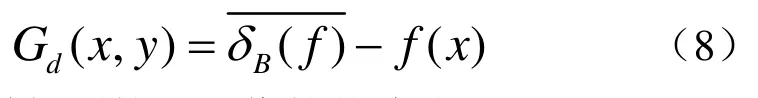
这样得到的是图像的外边缘。

还有一种边缘检测算子，称为膨胀腐蚀型边缘检测算子(也叫做形态学梯度)，表示如下

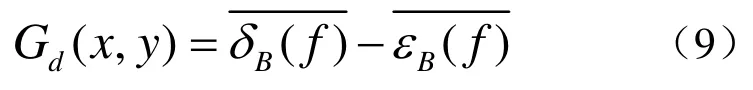
由于前两种方法都不抗噪，因此采用式(9)的算法，将上述改进的彩色图像形态学基本算子式(5)、式(6)直接进行梯度运算。

2 实验结果及分析

为了验证本文算法的有效性，在Matlab 7.0环境下和传统算法（Canny和Sobel算法）进行比较实验，原始图像为图1(b)加入10%椒盐噪声的lena图像，实验结果如图2所示。本文采用模板为3×3大小的结构元素进行边缘检测，结果如图2(d)所示，其中取n=3。

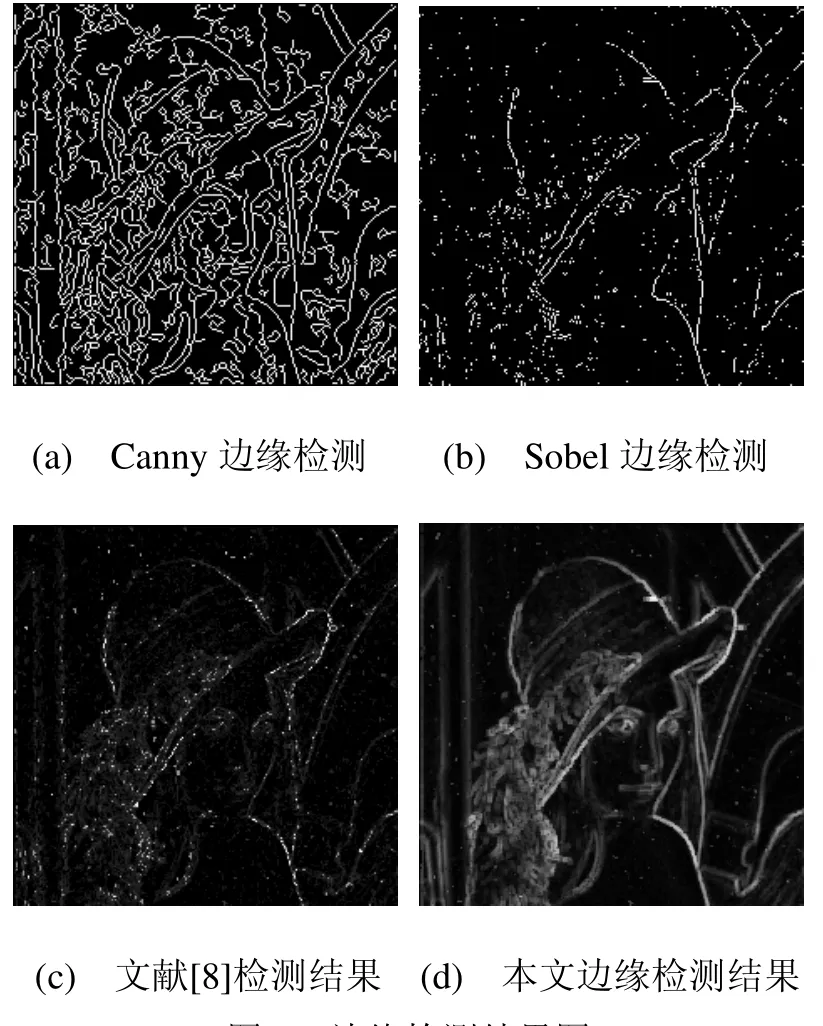
图2 边缘检测结果图

从图2可以看出，Canny算子容易过检测，将一些噪声也作为边缘的一部分（图2(a)），而Sobel边缘检测算子抗噪能力差，边缘容易漏检，且不连续（图2(b)）。文献[8]提出的彩色形态学梯度边缘检测结果（图2(c)）相对较好，但边缘细节不够丰富。本文提出的抗噪彩色形态梯度边缘检测算法（图2(d)）抗噪声能力最好，几乎不受噪声影响，而且检测的边缘连续平滑，轮廓更清晰，效果更好。

3 结束语

本文在RGB空间，用矢量的方法对彩色图像的颜色向量进行了排序。采用3×3结构元素，根据椒盐噪声污染图像的特点，求得最大值、最小值。与此同时，对噪声点进行了3次判断性移除，最终把信号值赋给了最大值、最小值，进而提出了改进的膨胀腐蚀算子。该算子有很强的抗噪性，可以直接通过梯度运算进行边缘检测。实验证明该算法检测出的边缘能够保留更多的细节，连续平滑，效果较好。

[1]KOSHAN A. A comparative study on color edge detection [C]//Proceedings and Asian Conference on Computer Vision. Singapore: IEEE, 1995: 574-578.

[2]范立男, 韩晓微, 徐心和. 基于HSI空间彩色图像多结构元形态边缘检测[J]. 工程图学学报, 2005, 26(2):155-156.

[3]王 宁, 张 颖. 基于 HSI空间的柔性形态学的彩色图像边缘检测[J]. 计算机应用, 2007, 27: 95-96.

[4]崔 屹. 图像处理与分析-数学形态学方法及应用[M]. 北京: 科学出版社, 2000: 146-149.

[5]GOUTSIA J, HEIJMANS H J, SIVAKUMAR K.Morphological operators for image sequences [J].Computer Vision Image Understanding, 1995, 62(3):326-346.

[6]尹星云, 王 峻. 基于改进的彩色图像形态学膨胀和腐蚀算子设计[J]. 计算机工程与应用, 2008,44(14): 172-183.

[7]EVANS A N, LIU X U. A morphological gradient approach to color edge detection [J]. IEEE Transactions on Image Processing, 2006, 15(6):1454-1463.

[8]EVANS A N. Mrphological gradient operators for color images [C]//Proceedings of the 2004 International Conference on Image Processing.Singapore: IEEE, 2004: 3089-3092.