简单树的结构矩阵及应用

张景晓

(德州学院 数学系，山东德州 253023)

1 简单树及其结构矩阵

1.1 简单树的规范化形式及其结构矩阵

定义设G是满足条件Δ(G)≤4的树，则称G是简单树，其中Δ(G)是G的最大度。设G是简单树，G中最长的链叫主链，连接主链两侧的链叫侧链，把图的主链横写在同一直线上，侧链垂直地连接在主链的两侧，并且约定侧链离主链端点最近的一端在左方，较远的一端在右方;当图的节点处只有1条侧链时，将该侧链连接在主链节点的上方;当图的节点处接有2个侧链时，较长的侧链接在该节点的上方，较短的侧链接在节点的下方，满足以上条件的图叫规范图。

根据实际应用的需要，可给规范图的顶点赋予权值，权值可以是任意实数，如取每个节点的度为其权值，得如图1的赋权图。

图1 赋权图

按照顶点赋权图的原样给出的矩阵(注意空白处用0填充)

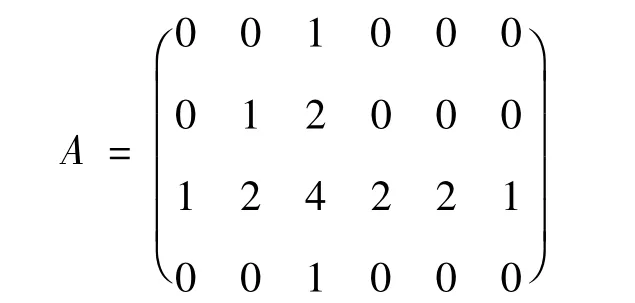
叫做图G的结构矩阵。

1.2 结构矩阵的一般化数学描述

为便于一般性理论研究和结果的推广，下面对结构矩阵给出一般性描述。

设

是某一m行n列的简单树的结构矩阵，其中A的第0行对应于图的主链，主链上方的行依次定义为第1，2，…，s行，主链下方的行依次定义为矩阵A的第－1，－2，…，－t行。用αi=(ai1，ai2，…，ain)表示矩阵 A 的第 i个(i= －t，－t+1，…，0，1，2，…，s)行向量，βj=(asj，as－1j，…，a0j，a－1j，a－2j，…，a－tj)T，表示A的第j(j=1，2，…，n)个列向量。分别表示矩阵A的行向量 αi和列向量 βj的1范数。

2 利用结构矩阵预测链状化合物的理化性质

以链烷烃的色谱保留指数的预测为例。由于链烷烃的分子骨架图就是满足条件的简单树图，因此可以根据系统命名原则，参照结构矩阵的书写规则，给出相应的分子结构图的结构矩阵，如2，4－二甲基戊烷，其隐氢图为

为便于更广泛和更深入地利用图的结构矩阵来研究物质结构与性能的关系，考虑到不同原子对物性的影响，取分子骨架图顶点原子的原子序数为其顶点的权值，根据分子拓扑学理论，不会影响结构与物性的研究，但能达到区分原子类型的目的。由于碳原子的原子序数是6，故化合物2，4－二甲基戊烷的赋权图为

按照赋权图的原样给出结构矩阵:

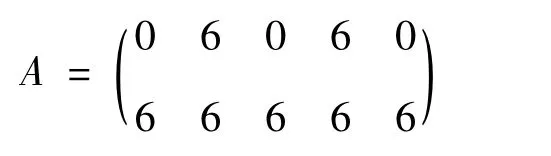
根据以上讨论，下面列出部分链烷烃的分子结构式及结构矩阵，见表1。

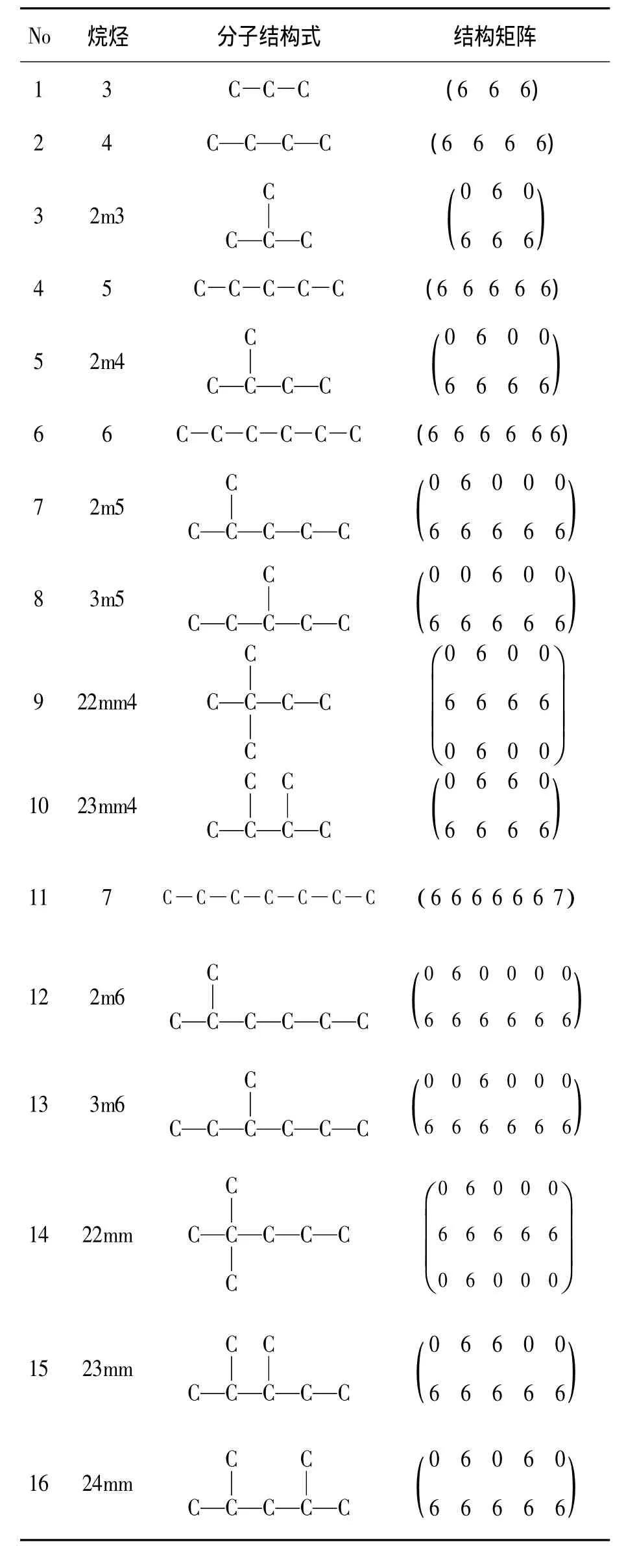
表1 部分链烷烃的规范化分子结构图及其结构矩阵

链烷烃分子的结构矩阵是分子结构图原样的量化，它相当于分子结构图的一张数码照片，结构矩阵的行数、列数反映了物质分子的整体规模，是对分子大小的宏观描述，结构矩阵的行向量列向量的1范数是对分子支化程度从纵横不同方向的细化描述，同时由于组成矩阵的行列向量的元素不同，所以矩阵的行列向量也反映了构成物质的原子类型以及连接各支链的空间方位的信息量。因此完全有理由将分子结构矩阵的行数m、列数n以及行、列向量的1范数pi，qj作为分子的结构信息指数。

根据30种链烷烃的结构矩阵，计算了矩阵的行数列数，以及矩阵行列向量的1范数列入表2。然后借助于SPSS软件剔除线性相关向量，由表2所列链烷烃的结构信息指数与其色谱保留指数实验值RIexp关联，进行多元线性回归，得以下回归方程:

其中:n=30是样本点数;r=0.999是复相关系数;s是标准偏差;F=1 089.293为 Fischer检验值。利用式(1)计算了30种链烷烃的色谱保留指数(见表2 RIcal)，实验值与预测值吻合的非常好。

由以上预测结果及预测统计量表明，本文所建立的简单树图的结构矩阵简单实用，可用于结构与物性的相关性研究，因此拓展了图论应用的新思路。

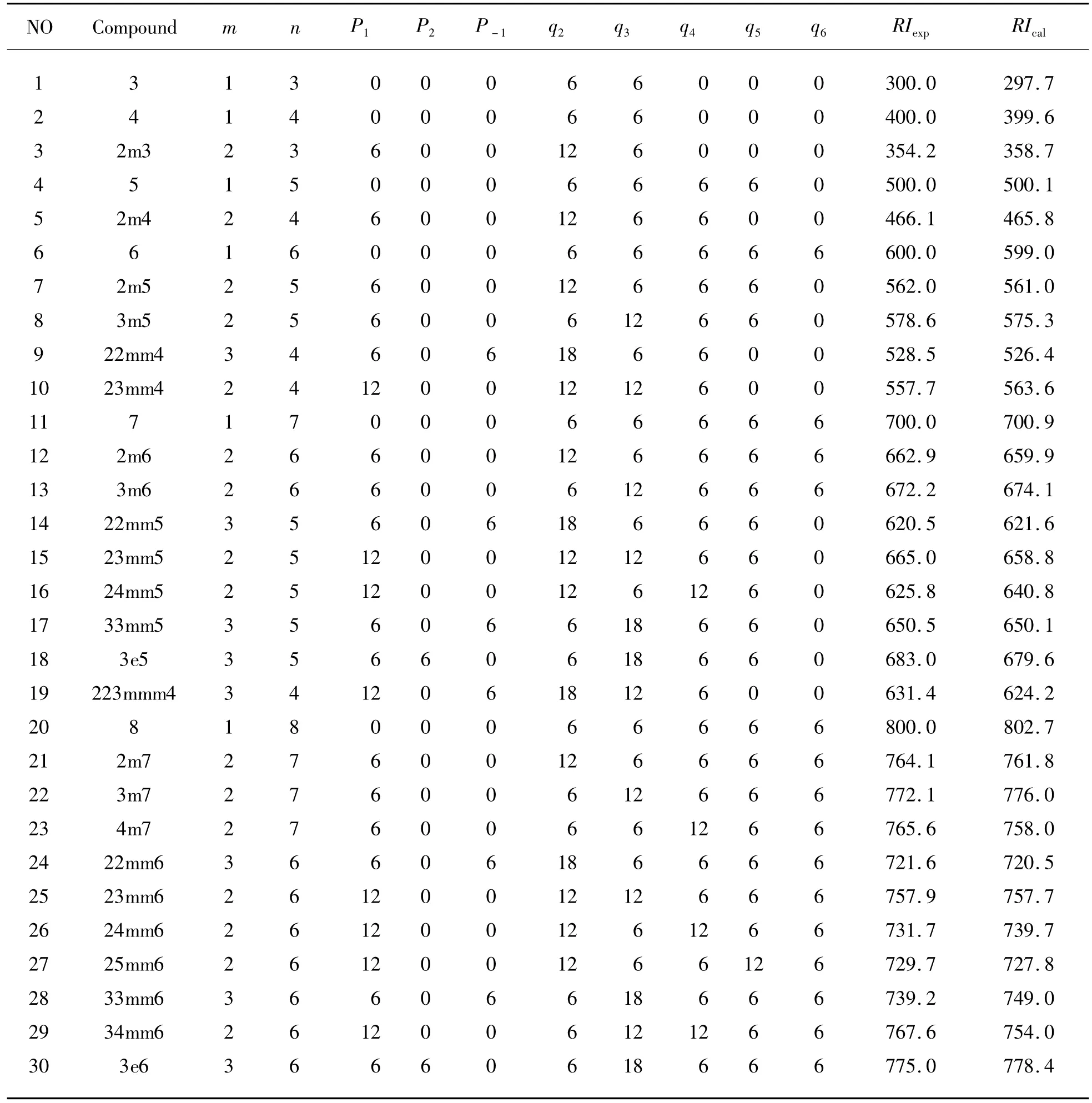
表2 30种链烷烃的结构信息指数及其色谱保留指数

［1］王树禾.图论［M］.北京:科学出版社，2004.

［2］刘缵武.应用图论［M］.长沙:国防科技大学出版社，2006.

［3］谢善梅.拓扑指数与烷烃色谱保留指数的定量相关性研究［J］.化学学报，2006，64(21):106 －109.

［4］许禄.应用化学图论［M］.北京:科学出版社，2000.

［5］邓辉文.离散数学［M］.北京:清华大学出版社，2010.