汽车传动系动态性能试验台驱动模拟方案的控制与仿真

刘力康 闻居博 董 逾

(1上海交通大学电子信息与电气工程学院,2上海交通大学汽车电子控制技术国家工程实验室,上海,200240)

1 引言

现代汽车工业正经历巨大变革,传动系作为汽车系统的核心部分,随着对汽车运行的可靠性要求日益提高,加之自动变速箱的广泛运用,对传动系统的特性和控制方法都提出了新的要求。因此对汽车传动系统试验台的能够为被测件提供真实的工况环境显得尤为重要。

国内外在传动试验台架的设计开发上已取得较好的成就,尤其是对负载电机部分的控制,如对汽车机械惯量的电模拟技术,来控制加减速过程的速度和加速度。但对于驱动部分,尤其是由交流电机代替汽车发动的试验台,相关文献确相对较少。然而随着环保意识、节能、节约成本意识的提高,以及交流变频调速技术的飞速发展,应用高性能交流调速电机代替实车的发动机的方式,在国内外得到了想当认可与应用。一个出色的驱动电机控制方案可以保证“电机-电机”离合器台架系统的动态性能表现与“发动机-电机”台架系统高度一致。双电机传动试验台还有以下几点优点：

◦ 无需燃油供给和尾气排放系统建设。消防设施建设标准比带内燃机的实验要低,因此能节约大量建造、运行及保养成本。

◦ 无需改变系统机械结构,只需发动机模型下载与相关参数标定,该台架系统能模拟各种发动机与负载情况。因此该台架系统有很强的灵活性,应用范围大。

因此本论文着重对台架驱动部分模拟发动机的静态与动态特性特性进行讨论,为传动试验台控制技术提供一个思路。

2 台架系统简介

本试验台系统通过变频技术控制两台交流异步电机,驱动离合器及变速箱转动,满足试验台在各种工况的性能要求。变频调速系统与PLC系统通过PROFIBUS网相连,这样变频调速系统就可实现远程控制和操作。同时,变频器中所有的电量及速度,转矩等实际数据均可加入到数据采集系统中。驱动系统使用在直流母线上进行功率平衡的电封闭方案,能量从较小的整流单元经直流母线流向驱动逆变单元,驱动电机带动机械传动装置。台架结构图见图1。

3 开环转矩控制算法

3.1 发动机特性曲线(静态特性)

为了能让试验台的驱动电机输出与真实发动机相同的特性,首先需要驱动电机的输出端能够根据发动机的特性曲线输出对应的扭矩。发动机特性曲线表示了发动机节气门开度,发动机曲轴转速与发动机输出转矩之间的关系。试验台驱动部分输出端有安装有一台扭矩传感器(量程为±500 Nm),该扭矩仪上的扭矩值对应的是驱动电机的输出值,同时也是被测件(自动变速箱)的输入扭矩。由于扭矩仪安装在驱动电机输出轴上(见图1),因此该扭矩与交流电机产生的电磁扭矩之间存在一个差值。PLC中的转矩控制器控制的是电机的电磁扭矩,因此如果不加以修正,扭矩传感器中读到的数值与发动机特性曲线中的转矩输出值会有差异,从而会影响到一些利用该扭矩进行控制的算法。

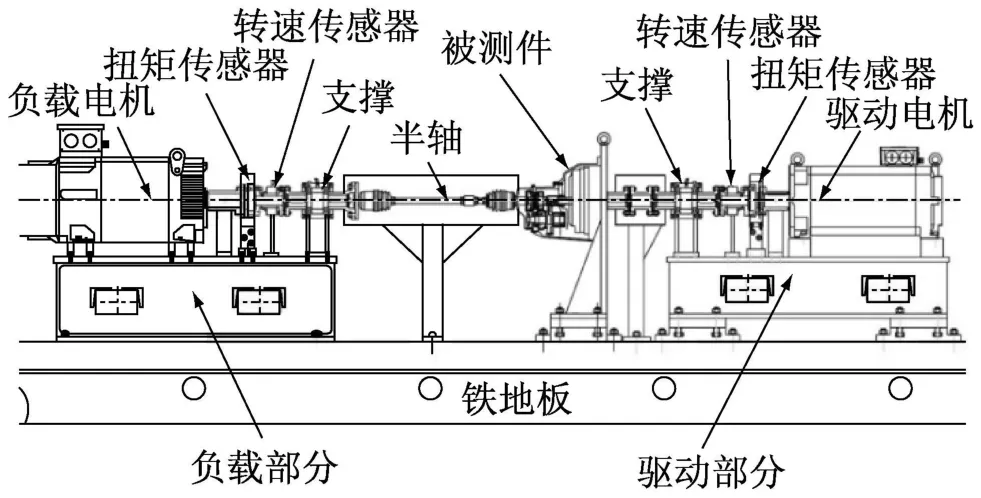
图1 台架结构图

3.1.1 闭环控制方法及其优缺点

修正该扭矩的方法主要有两种：一为闭环转矩控制,二是开环扭矩修正。由于电机控制系统为复杂的非线性系统,转矩闭环控制虽然能通过调整电磁扭矩将扭矩传感器处的扭矩控制到指定值,但该系统控制速度较慢,上升时间较长同时会有超调与振荡,因此利用闭环转矩控制来修正驱动电机输出扭矩的方法不适用于台架控制系统。

3.1.2 开环控制方法及其优缺点

开环转矩修正法则是基于大量实验,通过记录下不同转速,不同节气门开度情况下驱动电机的转矩输入值(通过查找发动机特性曲线而得到)与实际静态输出转矩值。然后运用二维插值算法,得到实测扭矩与电机扭矩输入值之间的关系,做出标定曲面。该曲面输入值为发动机特性曲线根据现在工况查到的理想输出扭矩值,输出值为实际发给电机的扭矩给定值。该方法不引入闭环控制控制器,而是通过标定曲面而来修正电机的电磁转矩给定值。此方法响应快,不存在扭矩振荡。然而由于线性插值的关系并不能保证所在有工作点上驱动部分扭矩输出值与期望扭矩完全一致,但经实验验证,误差在实验允许的范围之内。(见图2)

3.2 开环转矩惯量模拟控制模型

虽然开环转矩修正能够确保电机输出扭矩与发动机特性曲线上的相同,但特性曲线上的点只是代表了发动机静态的特性。单纯的扭矩修正无法保证驱动电机输出与发动机的动态特性也保持一致。由于真实发动机的惯量与摩擦阻力与台架系统的惯量与摩擦阻力并不相同,因此在不加任何其他补偿的情况下,驱动电机的动态转速或者加速度与真实发动机的转速与加速度不同,这样驱动电机是无法准确的模拟发动机动态特性的。

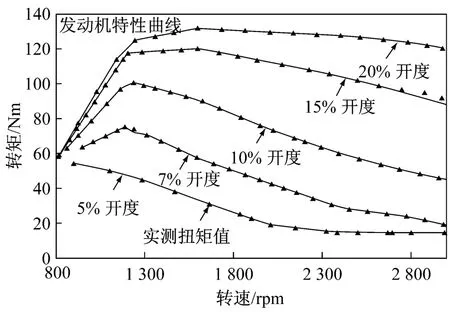
图2 台架上得到的发动机特性曲线

3.2.1 惯量模拟介绍

假设发动机的惯量为Jeng,Keng阻尼系数为,则：

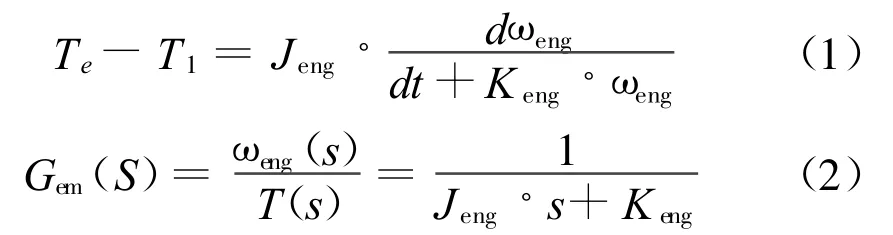
驱动电机的惯量为JD,阻尼系统为KD,则：

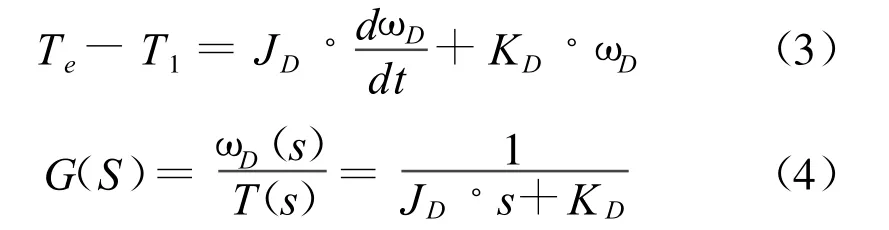
其中Te为驱动电机电磁扭矩或发动机输出转矩,T1为负载转矩,T为合转矩。

由传递函数可见,由于驱动电机惯量阻尼与要模拟的发动机的惯量阻尼不同,为了让驱动部分能模拟实际发动机的动态效果,首先需要通过实验得到驱动电机本身的惯量与阻尼系数,同时还要明确要模拟发动机的惯量阻尼参数。然后根据实际测量得到驱动电机输出转矩T1,采用电惯量模拟技术,计算得到驱动电机的电磁转矩Te,从而等效及补偿发动机的等效惯量和摩擦,使得

3.2.2 开环转矩补偿方法

开环转矩补偿的主要可以通过以下两种算法来实现。

逆模型方法一：如图3所示,该算法根据转速传感器得到的实时转速值ω,转速微分值,驱动系统逆模型G-1(s)以及模拟的发动机逆模型(s)计算出在转速ω和负载扭矩T1下,应该给驱动电机的扭矩期望值使得驱动部分的输出与模拟发动机系统相同。由于逆模型方法需要计算转速的微分值,而转速传感器的输出值存在噪音,因此不能直接用该数值进行微分计算。应该使用估计的驱动系统逆模型即根据估计的台架系统惯量阻尼系数计算得到估计的加速度该开环惯量模拟方法既需要驱动系统逆模型又需要发动机的逆模型,然而这两个模型一般都是复杂的非线性系统,要得到精确的逆模型需要对其进行复杂的系统辨识。若只用简单的惯量摩擦逆模型控制效果影响很大。(见图9)

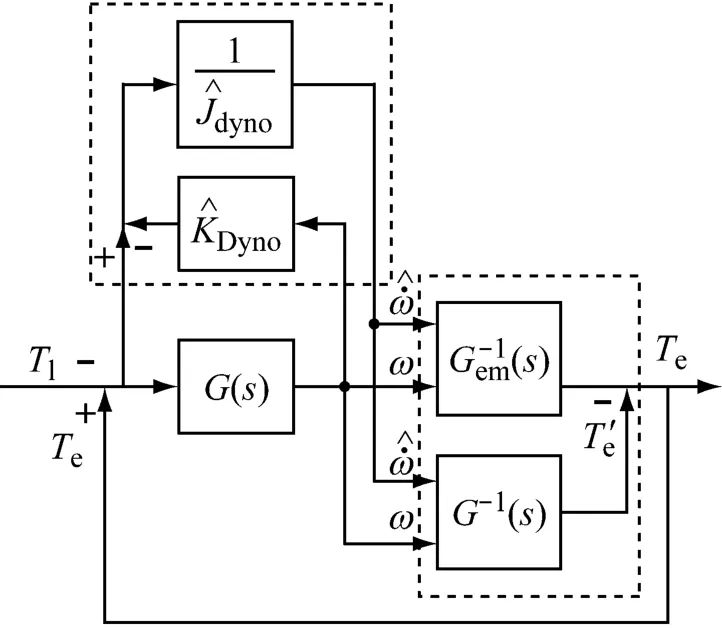
图3 开环转矩补偿(逆模型方法一)

逆模型方法二：如图4所示,扭矩传感器得到的扭矩通过发动机模型计算得到期望转速ωem,然后经过补偿器计算得到期望转矩值。若补偿器Gcomp(s)为驱动部分统逆模型G-1(s),则该开环系统的传递函数为：

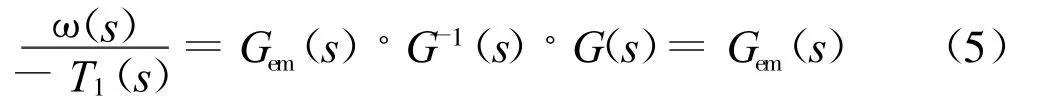
其中Gem为所要模拟的发动机系统传递函数。由公式(5)可见,该算法结构比逆模型方法一简单,无需计算微分,且只需得到准确的台架系统逆模型就可以准确的模拟发动机的动态响应。但由于非线性系统的逆模型存在建模的不准确性,因此该开环算法依旧不可避免的存在误差。(见图9)

图4 开环转矩补偿(逆模型方法二)

在Matlab/Simulink环境下运行车辆传动系模型,该模型包括发动机模型,驾驶员模型,自动变速箱模型与整车模型。如图6所示。后两者在整车环境下用来提供台架驱动电机的负载,而发动机模型则是由台架驱动电机模型以及对应的补偿算法所代替(见图5)。通过这样来验证上述两种开环转矩补偿方法的效果。

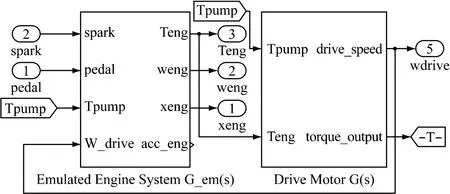
图5 发动机模型与台架模型

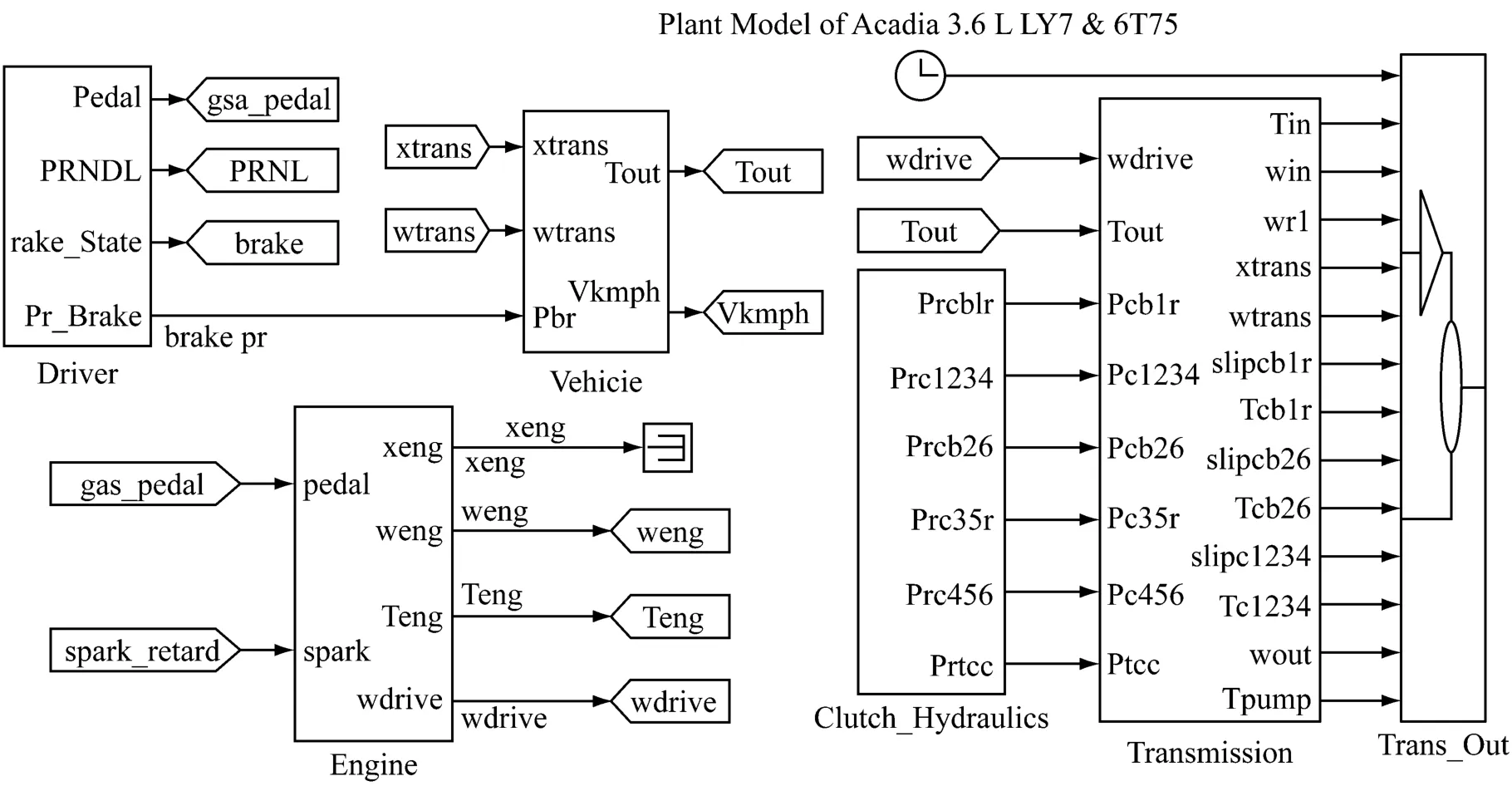
图6 GM整车模型

其中台架驱动电机部分为交流异步电机,其控制方法为基于转子磁链定向矢量控制,它的简化模型如图7所示。

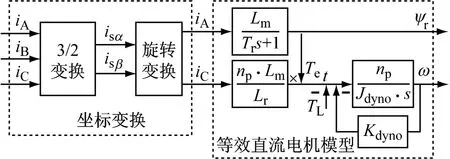
图7 等效直流电机模型

可见异步交流电机虽然能经过坐标变换等效成直流电机进行控制,但控制时由于变频器等可能产生滞后,同时等效直流模型里存在非线性环节,因此精确建模比较困难。需将该等效直流电机模型进一步简化,如图8所示。

此时交流电机的传递函数可以简化成：

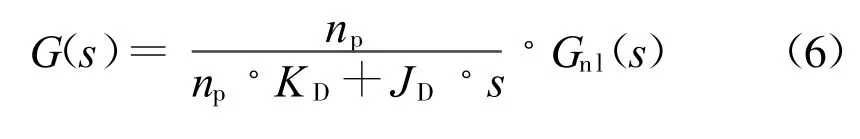
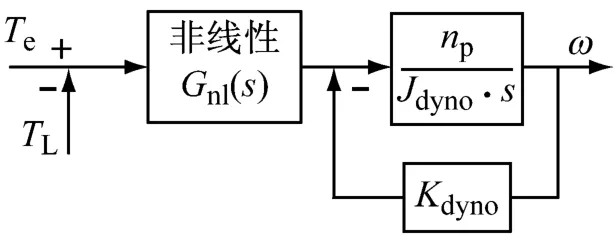
图8 交流异步电机的简化系统

其中np为级对数,KD为台架驱动部分的摩擦系数,JD为台架驱动部分的惯量。Gnl(s)为系统中存在的难以建模的非线性环节,包括控制延时,磁滞环节,饱和环节等。

图9为两种开环扭矩惯量模拟算法的仿真结果,其中蓝色实线为原整车系统的发动机曲轴转速与发动机输出扭矩。绿色点线与红色虚线线分别是运用两种不同的开环算法后驱动电机输出端的转速和扭矩。如图可见,非线性建模误差会对控制效果产生影响,而逆模型方法一需要运用两个逆模型,因此效果比起方法二来说有明显的不足。

4 转矩前馈加转速反馈控制方法

由于系统建模的不确定性,单单使用逆模型开环方法无法实现准确的动态模拟。因此可以将此开环通道用作前馈通道,同时引入转速PID控制,清除由于系统建模误差或者外界干扰造成的系统控制误差。提高控制精度及抗干扰能力。

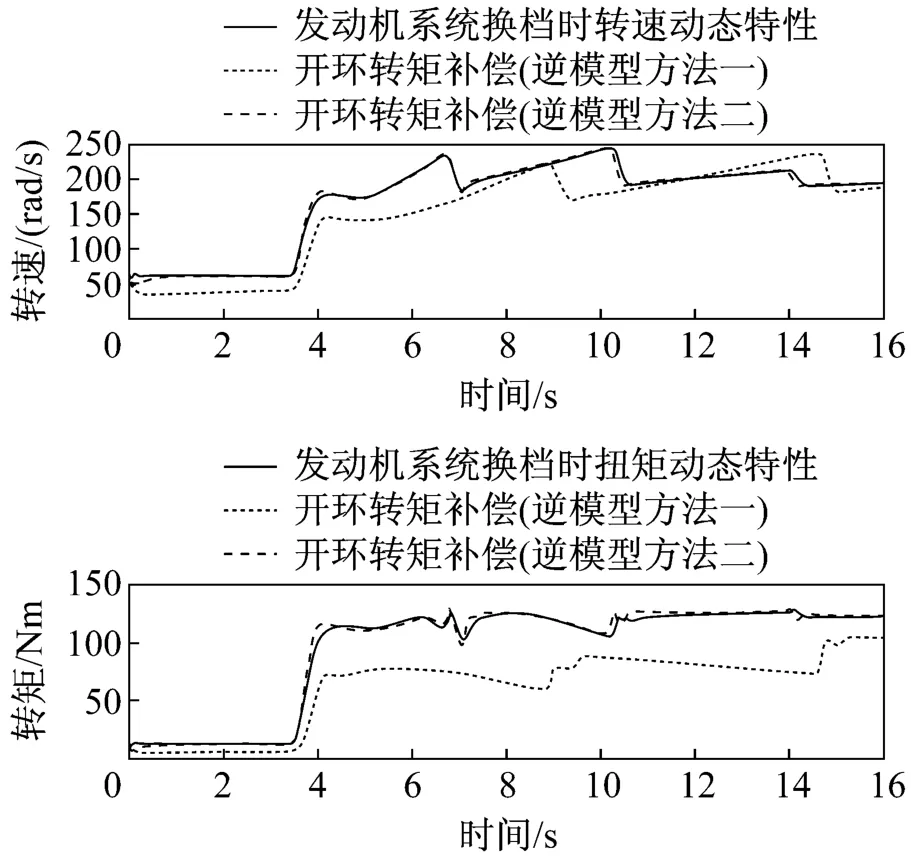
图9 两种开环扭矩惯量模拟算法的比较

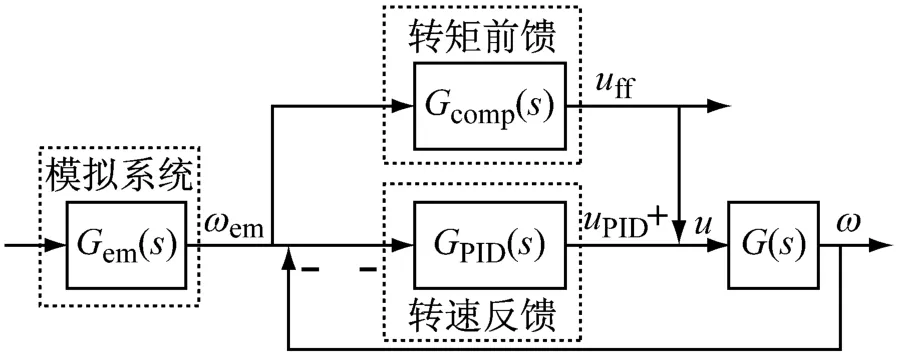
图10 转矩前馈加转速反馈的控制方法

前馈通道中的Gcomp(s)=G-1(s),因此在能得到精确驱动部分逆模型的情况下,控制效果和开环逆模型方法二相同。当逆模型存在误差的情况下,系统的传递函数为：

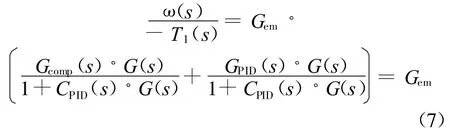
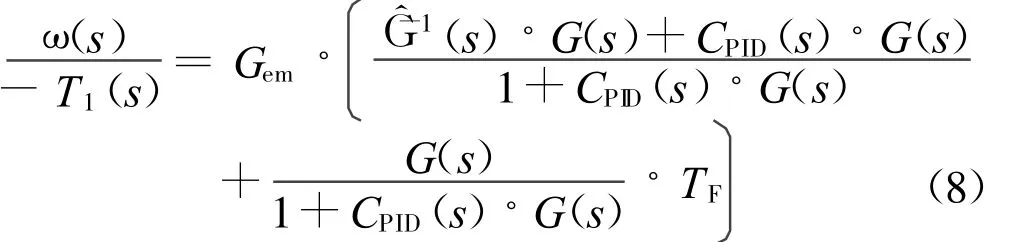
图11为转矩前馈算法在整车纵向动力学模型中的仿真结果,可见当台架系统为线性时不变系统且可以准建模型时,前馈通道使用逆模型即可实现准确的动态模拟(如下图绿色虚线所示)。若G(s)难以准确建模,则可用估计模型的逆模型或者其静态非线性(如Hammerstein模型的静态非线性部分)部分作为其前馈[6]。

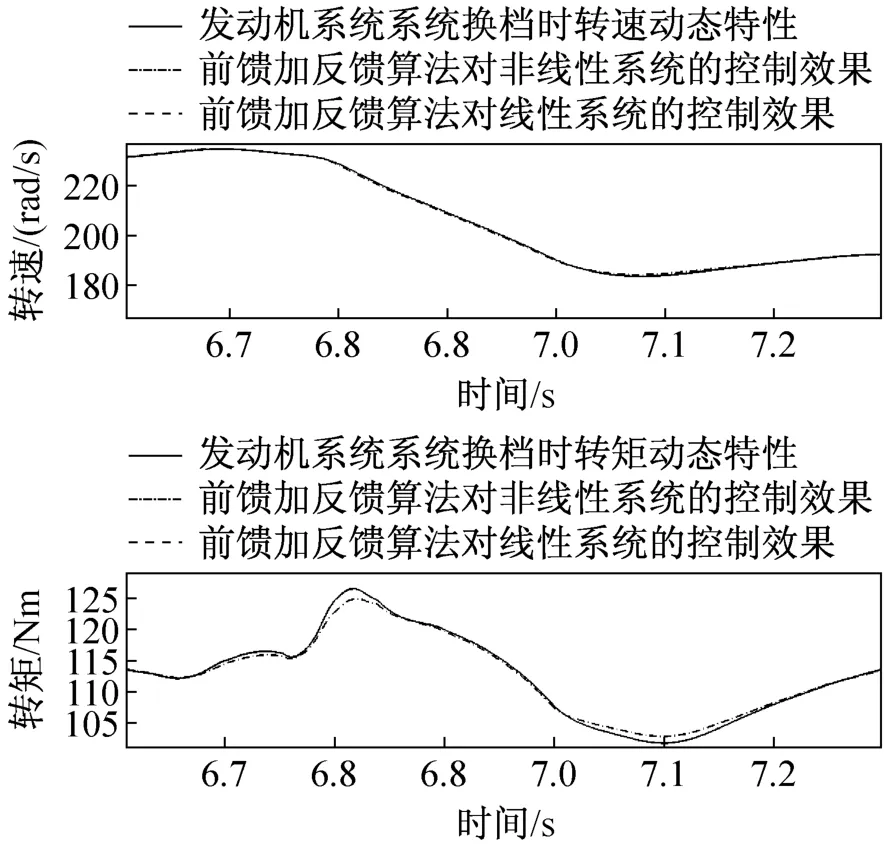
图11 转矩前馈加转速反馈控制方法仿真

由于系统建模的不准确性,该算法虽然能较好的对转矩和转速分别进行控制,稳态时效果很好。但动态时不能完全抵消台架系统的动态特性。如图11所示,变速箱进行2-3换档的时候,转速跟踪控制效果显著,但输出扭矩(黑色虚线)与要原系统(蓝线)依旧存在微小偏差。从系统传递函数角度分析,是由于逆模型建模不够准确,同时又引进了转速闭环,此时该系统的传递函数不完全等于要模拟的Gem。虽然动态特性并不能完全相同。但由于闭环系统的存在,通过选择合适的PID参数,能够保证实际控制系统的稳定性,抗干扰性与鲁棒性,这些特性对真实台架系统控制尤为重要。

5 带延时的系统控制方法

在此台架控制系统中,PLC判断外围信号准备条件,通过Ethernet OPC协议,接收来自上位机(Labview HMI)的控制指令,经过处理后通过Profibus通讯将控制命令送到变频器控制电机的起动停止及工作方式。上位机部分用来发出电机的起动停止命令及速度或转矩给定值,显示电机的当前状态,如电机的转速、转矩、电压、电流和功率等,并对NI设备所采集到的数据值进行处理并保存。其中DP Profibus的传输速率很快,最快可以达到12 Mbps,然而基于以太网的OPC协议的数据更新频率实际测量最快只能达到20 Hz。

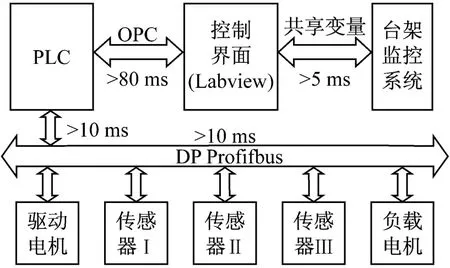
图12 台架系统框图

由于前馈通道的转矩给定值,以及闭环转速期望值等都是经过Labview HM I主程序计算得到,并通过以太网OPC协议发送给PLC,其通信延时在80-120 ms左右。同时由于在控制系统的反馈通道中,信号采集使用的传感器信号常常需要经过低通滤波才能参与反馈控制,而滤波算法也必定带有延时。由于延时的存在,普通的控制算法如PID不一定再适用,有时甚至会出现不稳定的情况。[5]

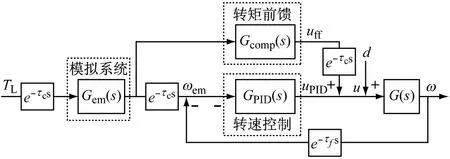
图13 带通信和反馈延时的控制系统框图

由图推导带有延时的系统传递函数：

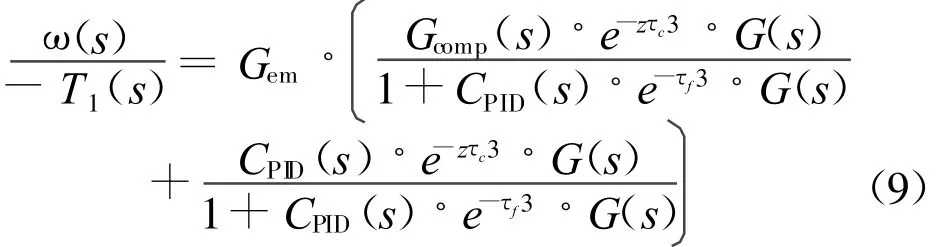
其中e-τf3为反馈通道延时,e-τc3为通讯延时。

从传递函数中可以看出,对于带有延时的系统,其传递函数中分母中含有纯滞后环节e-τc3,随着的增大,相位滞后增大,系统的稳定性降低,控制质量下降。

如果在被控对象上再并联上一个补偿器补偿掉反馈延时通道中的纯滞后,这种补偿器通常称为Smith预估器。但在实际运用中Smith预估器并不接在被控对象上,而是反向并接在控制器上取代了传统的PID调节器。[4]

图14 带有Smith预估器的控制系统

加入了Smith预测器后的系统传递函数为：

若前馈补偿器的台架模型的逆模型G-1(s),

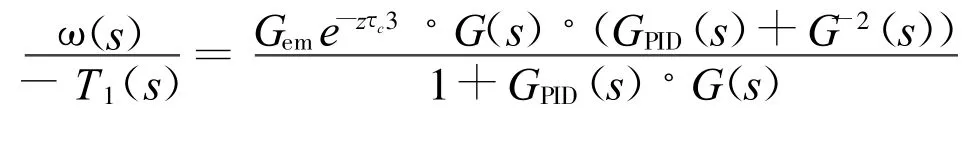
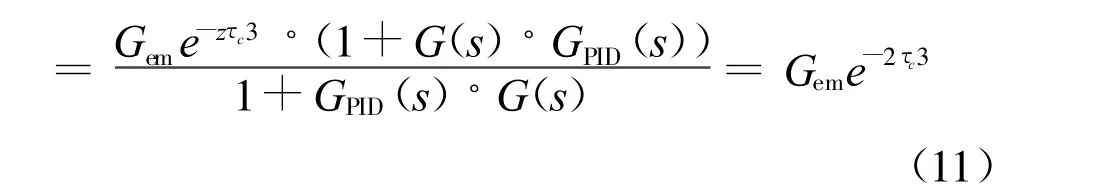
误差传递函数为：

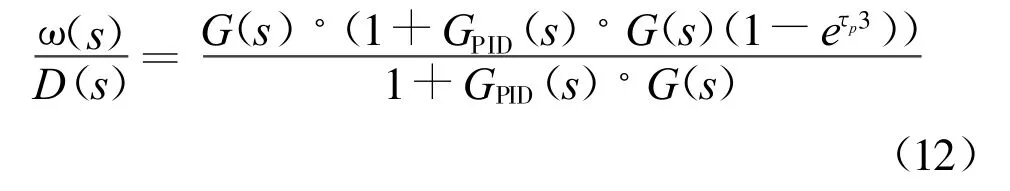
由上述两式可知,控制系统无论是在设定输入T1或者系统干扰d作用下,闭环传递函数的特征方程相同,都为1+GPID(s)◦G(s)=0。闭环系统的动态特性主要决定于特征方程,因此经过补偿的系统动态控制效果与上文所提到的转矩前馈加转速反馈方法一样,原先的控制器仍然适用,不会影响系统的稳定性,只是控制时间长了2τc秒。仿真控制效果见图15。

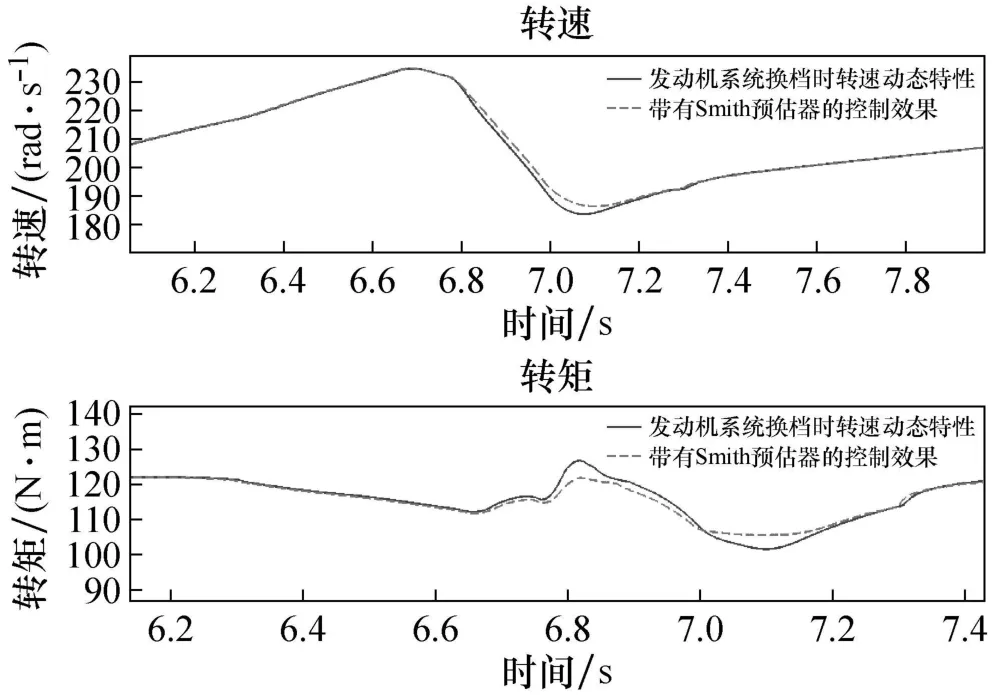
图15 带Smith预估器的控制效果(80 ms通信延时)

6 结论

本文一次介绍了发动机特性曲线的台架实现,两种电惯量阻尼的模拟方法(开环转矩修正或者带有前馈通道的闭环转速控制),使得台架系统与发动机系统在动态性能上有足够的相似性。本文在最后提出了运用Smith预估器在传动台架上的运用,通过它来抑制系统延时对控制系统吸能。本文为汽车传动试验台架驱动部分的控制开发提出了可供参考的思路、流程与解决方案。

[1]Z.Hakan Akpolat and Greg M.Asher“Dynamic Emulation of Mechanical Loads Using a Vector-Controlled Induction Motor– Generator Set.” IEEE transaction on industrial electronics,Vol.46,No.2,April 1999.

[2]M.Rodic,K.Jezernik and M.Trlep,“Dynamic emulation of mechanical loads：an advanced approach” ,IEE Proc.-Electr.Power Appl.,Vol.153,No.2,March 2006.

[3]R.W.Newton,“Emulating dynamic load characteristics using a dynamic dynamometer,”in Proc.Int.Conf.Power Electronics and Drive Systems,1995,vol.1,pp.465–470.

[4]杜 锋,钱清泉,杜文才,基于新型Smith预估器的网络控制系统,西南交通大学学报,第45卷第1期,2010年2月.

[5]赖 伟,喻寿益.网络延时对PID控制系统性能影响的分析[J].信息与控制,2007,36(3)：302-307.

[6]L.Ljung：System Identification-Theory For the User,2nd ed,PTR Prentice Hall,Upper Saddle River,N.J.,1999.