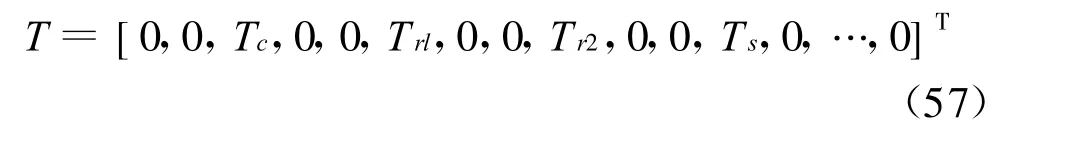复式行星齿轮传动装置的自由振动特性(二)

4.4 每排多于三个行星齿轮的CPGT：N≥3

固有频率和相应的振动模式列于表4,分类为以下三种：

1.10 个固有频率：对于不同数目行星齿轮N有阶mf=1,除零固有频率外,导致它们的值随附加行星齿轮数而增加。它们连带振动模式有行星架,齿圈1,齿圈2和太阳轮的纯常见的转动变形。该行星齿轮具有同相位相同运动(图8),这些模式称为转动模式。

2.10 个固有频率：对于不同行星齿轮数目N有阶mf=2,随着N增加有一些固有频率单调增加,而另一些则单调减少。在相应的振动模式,行星架,齿圈1,齿圈2和太阳轮有纯移动,此外注意到以下有关之间变形,对于重复模式：ui1=vi2和vi1=-ui2,i=c,r1,r2,s其中(ui1,vi1)是第一模式中常见的变形,而(ui2,vi2)是第二模式内最常见的变形,该行星齿轮变形的总和等于零(图9),这些模式称为移动模式。

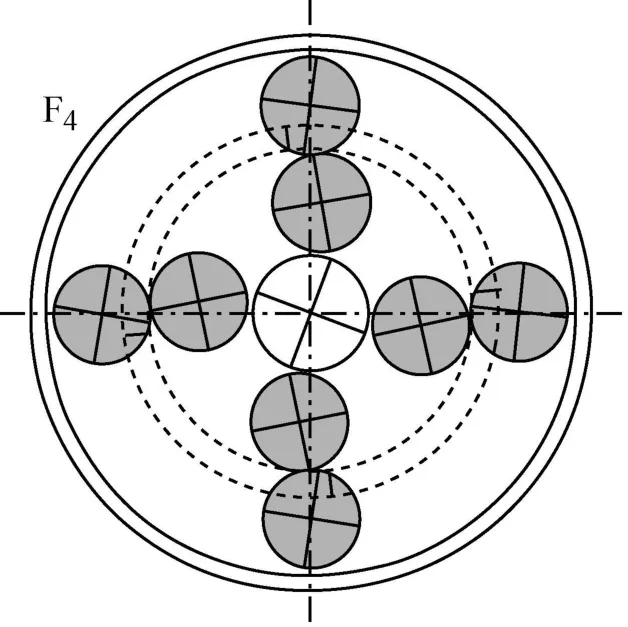
图8 转动模式的模式形态F4：相对行星齿轮同相位(相同变形)反相位(相反变形)Fig.8 Mode Shapes for rotational mode F4：the opposite planets are in-phase(same deflections)are counter-phased(opposite deflections)

图9 移动模式的模式形态F2和F3：行星齿轮相对Fig.9 Mode Shapes for translational modes F2and F3：the opposite planets

3.6 个固有频率：如果只有N＞3,有阶mf=N-3,其有关连的振动模式称为行星齿轮模式,因为行星架,齿圈1,齿圈2和太阳轮不运动,在该模式仅行星齿轮发生运动,相对行星齿轮为同相位(具有相同的变形),所有行星齿轮变形的总和等于零(图10至12)。

对于N=4,5和6,表4示最多有26个固频率;增加行星齿轮只有改变行星齿轮模式固有频率的多重性。

在Lin和parker[4]著作中可以找到本结果的论证,该作者们检测了三种固有频率并指出了它们的多重性。

4.5 行星齿轮布置第二排的影响

在行星齿轮第二排(13°)引起角位置的改变如图13所示,注意到由于行星齿轮b角位置α1b对固有频率稍有影响,但其类型仍保持不变如表5所示。

图10 移动行星齿轮a模式的模式形态F10：在本模式行星齿轮a不转动Fig.10 Mode Shapes for translational planet-a mode F10：the planets-a do not ratate in this mode

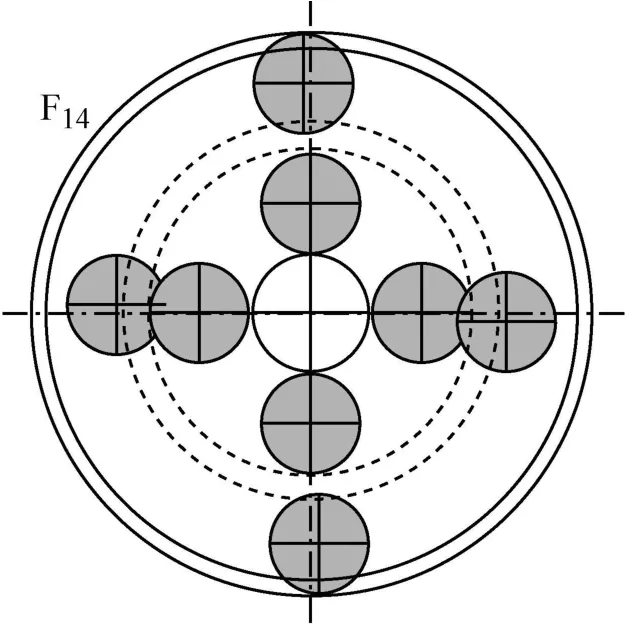
图11 移动行星齿轮b模式的模式形态F14：在本模式行星齿轮a不动Fig.11 Mode Shapes for translational planet-b mode F14：planets-a do not move in this mode

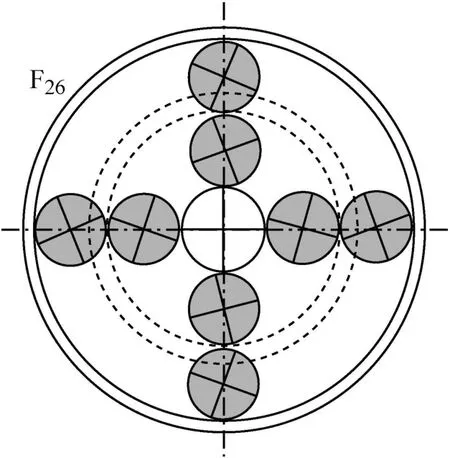
图12 转动行星齿轮模式的模式形态F26：在本模式所有行星齿轮不移动Fig.12 Mode Shapes for rotational planet mode F26：all planets do not translate in this mode

4.6 行星架转动速度的影响

图14示与行星架转速有关的一些固有频率的评估。可注意到对于行星架高速,移动的固有频率分为两不同的分支之一,而行星齿轮和转动固有频率保持不变,该分支随行星架转速增大而变大。

图13 行星齿轮b角位置α1bFig.13 Planet-b angle position α1b

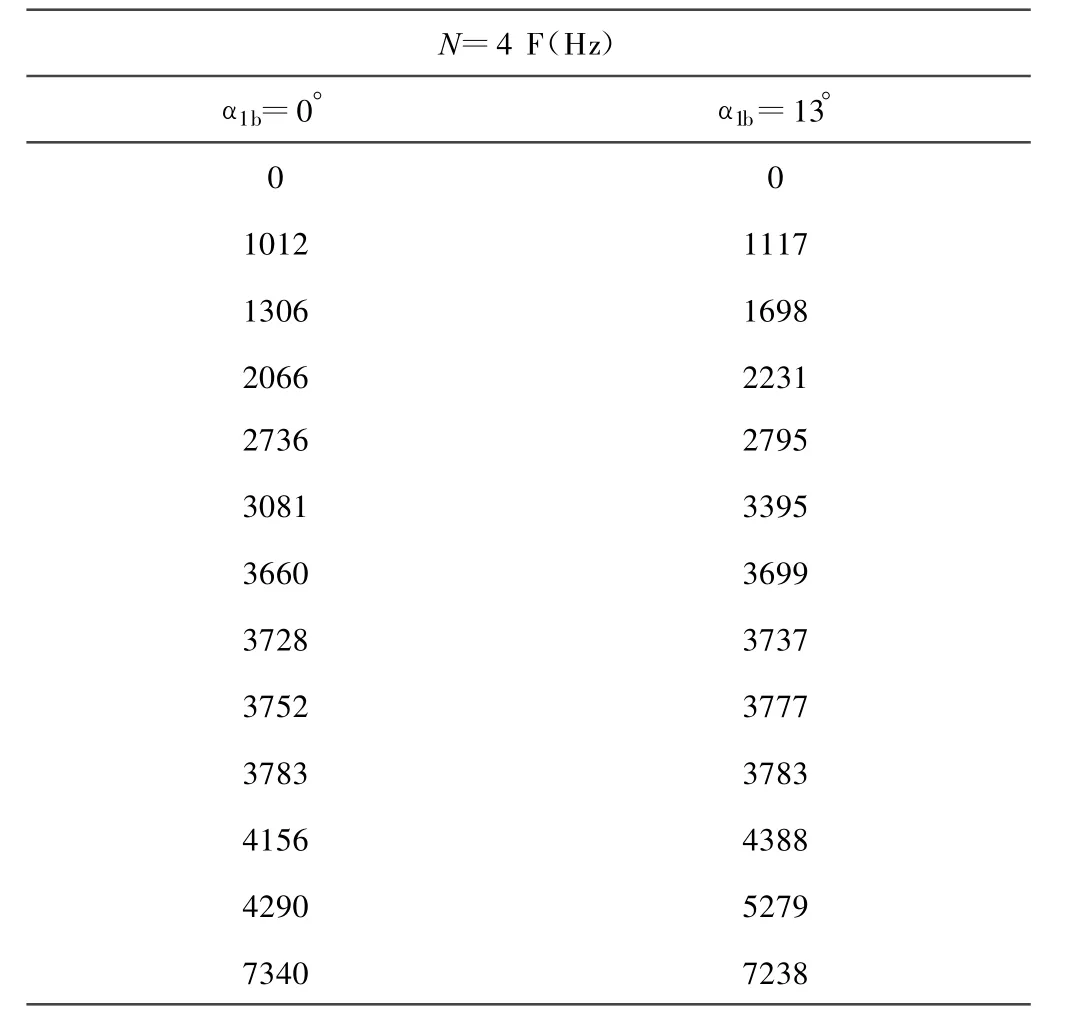
表5 对于行星齿轮b角位置α1b=0°和α1b=13°固有频率的变化Table 5 The variation of natural frequencies for planet-b angle positions：α1b=0°and α1b=13°

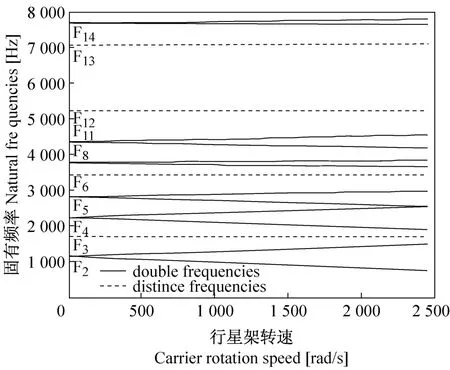
图14 行星架转速Ωc与固有频率间关系Fig.14 Natural frequency versus the carrier rotation speed Ωc

5 结论

本文开发了CPGT的一个平面动力学模型,导出运动方程式为一矩阵形式,采用齿轮啮合刚度的平均名义值计算固有频率和振动模式。它表明固有模式按照其固有的移动和转动可以分为三类。同时它还表明该固有频率对陀螺效应是敏感的。概括地观察到CPGT的最常见特性在动力学响应方面是十分重要的。(谷雨译自proc.IMechE 2008 Vol.222 partc：J.Mechanical Engineering Science)

[1]Gott G.Changing gears：the development of the automatic transmission,1991(Society of Automotive Engineers,Warrendale,PA,USA).

[2]Deniels J R.New generation drivetrains,1995(The E-conomist Intelligence Unit,UK).

[3]Hidaka T,Terauchi Y,and Fuji M.Analysis of dynamic tooth load on planetary gear.Bull.JSME,1980,23：315-323.

[4]Lin J,and Parker R G.Analytical characterization of the unique properties of planetary gear free vibration.J.Vibr.Acoust.1999,121：316-321.

[5]Houser D R.Gear noise state of the art.In Proceedings of the 17th International Conference on Noise Control Engineering,Avignon,France,30 August-1 September 1988,vol.2,pp.601-606.

[6]White R J,Exploration of a strategy for reducing gear noise in planetary transmissions and evaluation of lase vibrometry as a means for measuring transmission error.PhD Thesis,Department of Mechanical and Aerospace Engineering,Case Western Researve University,Janvier,2006.

[7]Pearce W J,Nilsen M A,and Rouverol W S.Reducing gear noise excitation.In Proceedings of the 2nd World Congress on Gearing,Paris,3-5 March 1986,vol.1,pp.587-598.

[8]Muller W H.Epicyclic drive trains,1982(Wayne State University Press,Detroit).

[9]Kahraman A.Free tortional vibration characteristics of compound planetary gear sets.Mech.Mach.Theor,2001,36：953-971.

[10]Hbaieb R,Chaari F,Fakhfakh T,and Haddar M.Three dimensional model for a helical planetary gear train vibration analysis.Int.J.Eng.Simul.,2005,6：32-38.

[11]Kasuba R,and August,R.Gear mesh stiffness and load sharing in planetary gearing.In the ASME 4th Power T ransmission Conference,Cambridge,Massachusetts,1984,Paper 84-DET-229.

[12]Haris L M S.Impact of system-level factors on planetary gear set behaviour.PhD Thesis,Graduate School of the Ohio State University,2007.

[13]Hbaieb R,Chaari F,Fakhfakh T,and Haddar M.Dynamic stability of a planetary gear train under the influence of variable meshing stiffnesses.Proc.IMechE,Part D：J.Automobile Engineering,2006,229(D12)：1711-1725.

[14]Lin J,and Parker R G.Parametric instabilities in planetary gears under mesh stiffness variations.J Vibr.Acoust,2000,249(1)：129-146.

[15]Lin J,and Parker R G.Structured vibration characteristics of planetary gears with unequally spaced planets.J Sound Vibr.,2000,233(5)：921-928.

[16]Howells R W.Transmission design with finite element analysis,Parts 1-3,1978(US ArmyResearch and Technology Laboratories,USA)(USARTL-TR-78-2A and 2B).

[17]Abousleiman A,and Velex P.Ahybrid 3D finite element/lumped parameter model for quasi-static and dynamic analyses of planetary/epicyclic gear sets.Mech.Mach.Theory,2006,41：727-748.

[18]Parker R G,Agashe V,and Vijayakar S M.Dynamic response of a planetary gear system using a finite element/contact mechanics model.ASME J.Mech.Des.,2000,122：304-110.

[19]Chaari F,Baccar W,Abbes M S,and Haddar M.Effect of spalling or tooth breakage on gearmesh stiffness and dynamic response of a one-stage spur gear transmission.Eur.J Mech A：Solids,2008,27(4)：691-705.

附录1 Appendix 1

符号 Notation a 长行星齿轮long planet b,d 短行星齿轮short planets c 行星架carrier diag 对角线矩阵diagonal matrix 动能kinetic energy 势能potential energy G 陀螺矩阵gyroscopic matrix h 接触比contact ratio 元件 j的惯量的极质量矩 polar mass moment of inertia of element j K(t)总时间变化刚度矩阵total time-varying stiffness matrix(t)总时间变化齿轮啮合刚度矩阵 total time-varying gearmesh stiffness matrix K0 名义齿轮啮合刚度矩阵 mean gearmesh stiffness matrix(t)时间变化齿轮啮合刚度矩阵 time-varying gearmesh stiffness matrix 轴承刚度矩阵bearing stiffness matrix 向心力刚度矩阵centripetal stiffness matrix kabi(t)行星齿轮ia-行星齿轮ib齿轮啮合刚度planet-ia-planet-ib gearmesh stiffness 元件j的轴承刚度bearing stiffnesses of element j 元件 j扭转刚度 torsional stiffness of element j kr1i(t)齿圈1-行星齿轮ia齿轮啮合刚度ring-

1-planet-ia gearmesh stiffness 齿圈2-行星齿轮ib齿轮啮合刚度ring-2-planet-ib gearmesh stiffness 太阳轮-行星齿轮ia齿轮啮合刚度 sunplanet-ia gearmesh stiffness 行星齿轮轴承刚度 bearing stiffnesses of planets md 模数module mf 固有频率多重性multiplicity of natural frequencies M 质量矩阵mass matrix 元件 j质量 mass of element j N 行星齿轮数number of planets p 整数 number of integers q 系统自由位移矢量 freedom displacement vector of the system 元件 j自由位移矢量 freedom displacement vector of element j r1 齿圈1 ring gear 1 r2 齿圈2 ring gear 2 元件 j基圈半径 base circle radius of element j s 太阳轮sun gear T 外力矢量external forces vector 作用元件j转矩torque applied to element j 元件 j移动自由度 translational degrees of freedom element j

Zj 元件j齿数teeth number of element j α 压力角 pressure angle 行星齿轮ib角位置planet-ib angular position 行星齿轮ia轴承相对径向和切向位移relative radial and tangential planet-ia bearing displacements 行星齿轮ib轴承相对径向和切向位移relative radial and tangential planet-ib bearing displacements 行星齿轮ia和行星齿轮ib相对齿轮啮合位移relative planet-ia and planet-ib gearmesh dis-

placement 齿圈1和行星齿轮ia齿轮啮合位移 relative ring-1 and planet-ia gearmesh displacement Δrib 齿圈2和行星齿轮ib齿轮啮合位移 relative ring-2 and planet-ib gearmesh displacement 太阳轮和行星齿轮ia齿轮啮合位移 relative sun and planet-ia gearmesh displacement 元件j转动自由度rotational degrees of freedom of element j Φ 固有值矩阵eigenvalue matrix 固有频率natural frequency 行星架角速度carrier angular speed

附录2 Appendix 2

采用Lagrange公式求得运动方程式,无阻尼,自然的动力学模型如图2所示的Lagrange公式为

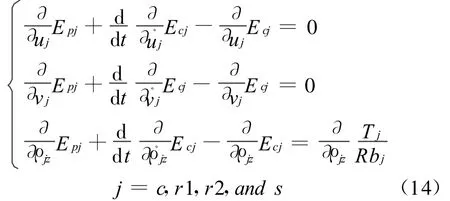
式中Epj,Ecj和Tj分别为元件j的动能,势能和外加转矩,对于行星齿轮,Lagrange公式求得

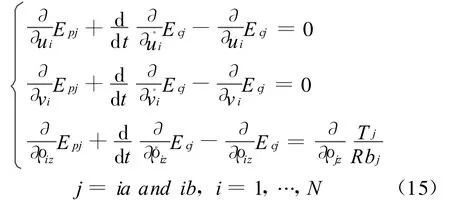
行星架,齿圈1,齿圈2,太阳轮,行星齿轮ia和行星齿轮ib的运动方程式为

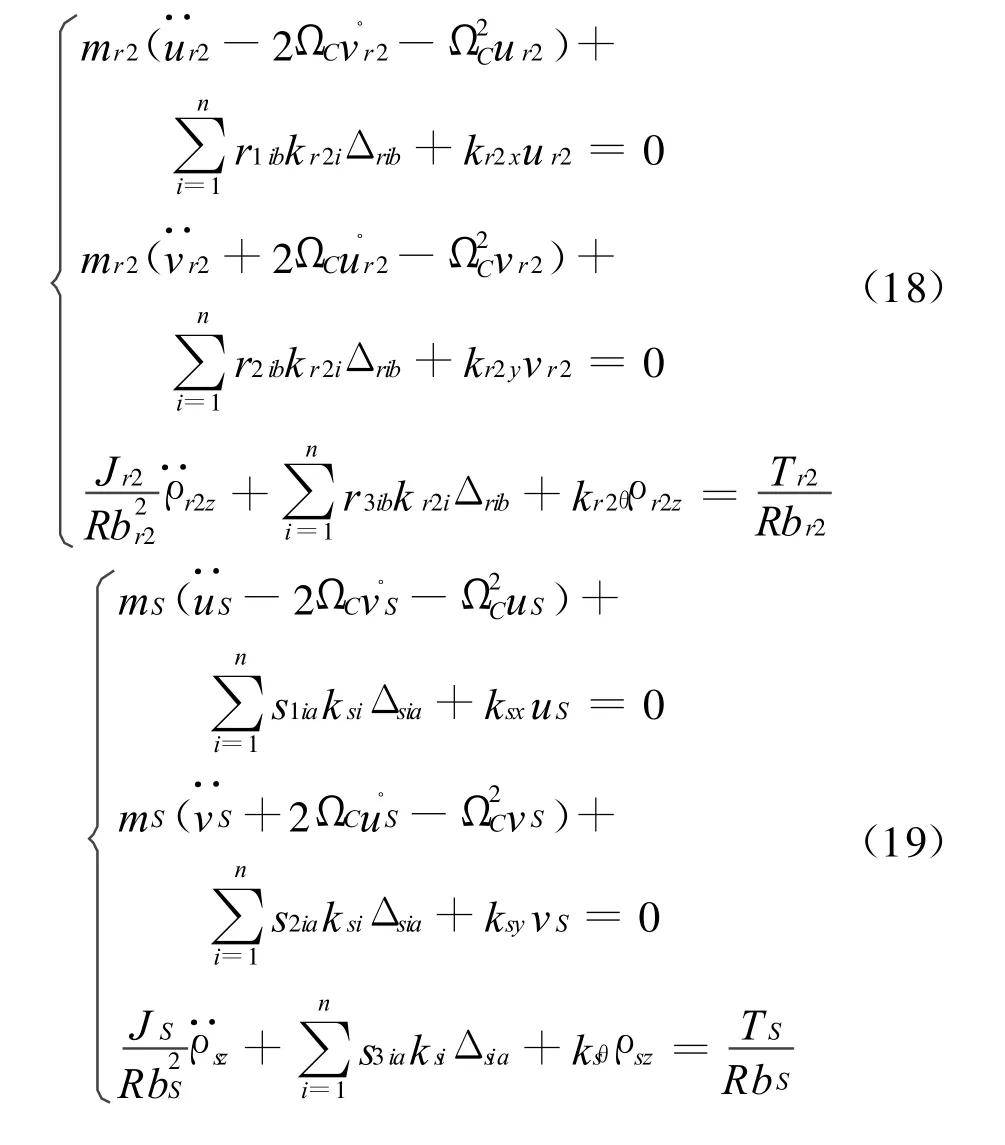
附录3 Appendix 3

位移矢量为

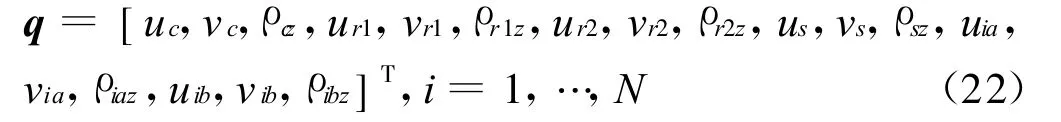
外加转矩矢量为

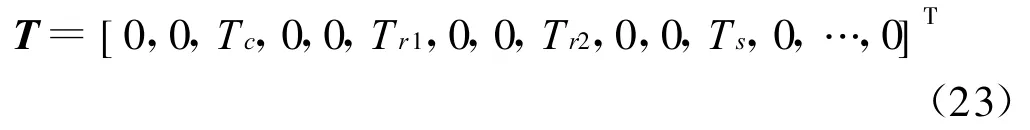
质量矩阵为

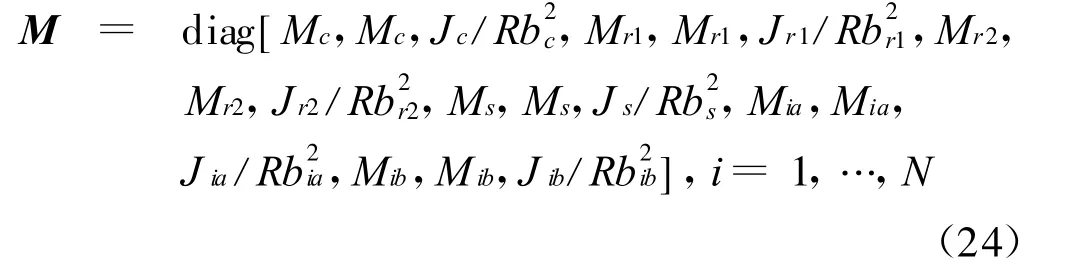
陀螺矩阵为

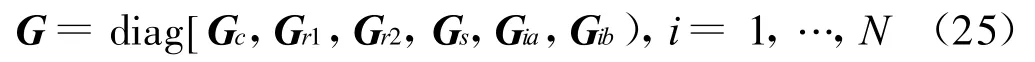
轴承刚度矩阵为

间心力矩阵为

接触比h,它是由两齿轮接触之间平均轮齿副数确定的,是估算齿轮啮合刚度的一个重要的系数。事实上,对于低接触比(h＜2)的情况,观察到的接触轮齿对数波动为一对或二对。由它可求出时间变化的齿轮啮合刚度Ke(t)。考虑到这种变化主要是变速箱的激励源,并引起振动和有害声响的放出。考虑轮齿数为Zpi的小齿轮的转速,其齿轮啮合周期(秒)确定为

由单对齿轮啮合刚度逐点迭加计算时间变化齿轮刚度如图4所示,最大刚度值相应于两对齿接触由(pTe)到(h-1)(pTe)求得,而最小值相应于一对齿接触由(h-1)(p)到((p+1))求得,p为整数[19]

在上述公式中啮合刚度函数可表示为

陀螺矩阵为

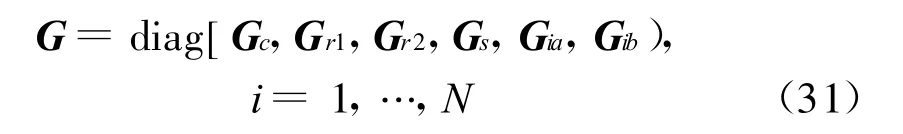
式中

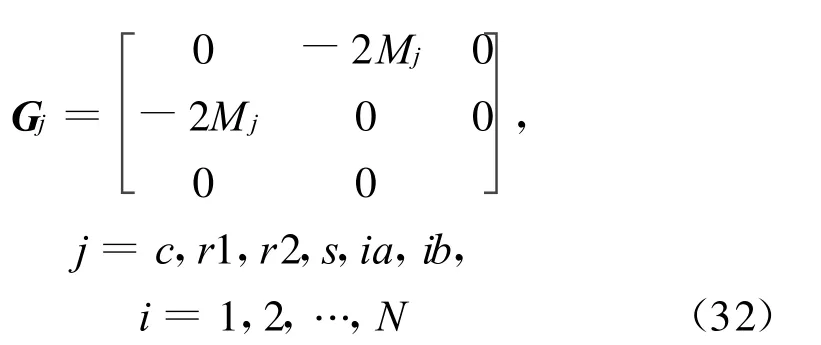
轴承刚度为

其中

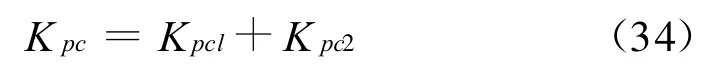
其中

向心力矩阵为

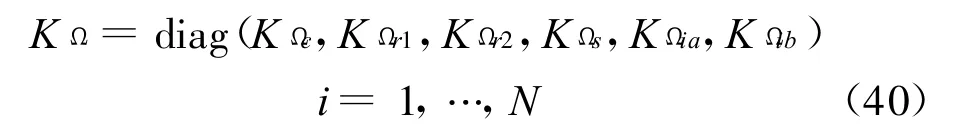
式中

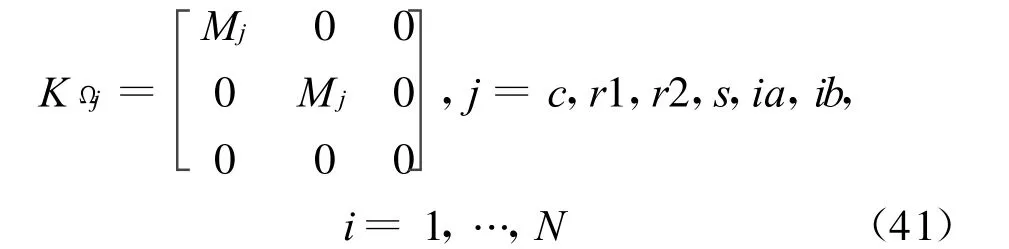
时间变化齿轮啮合刚度矩阵

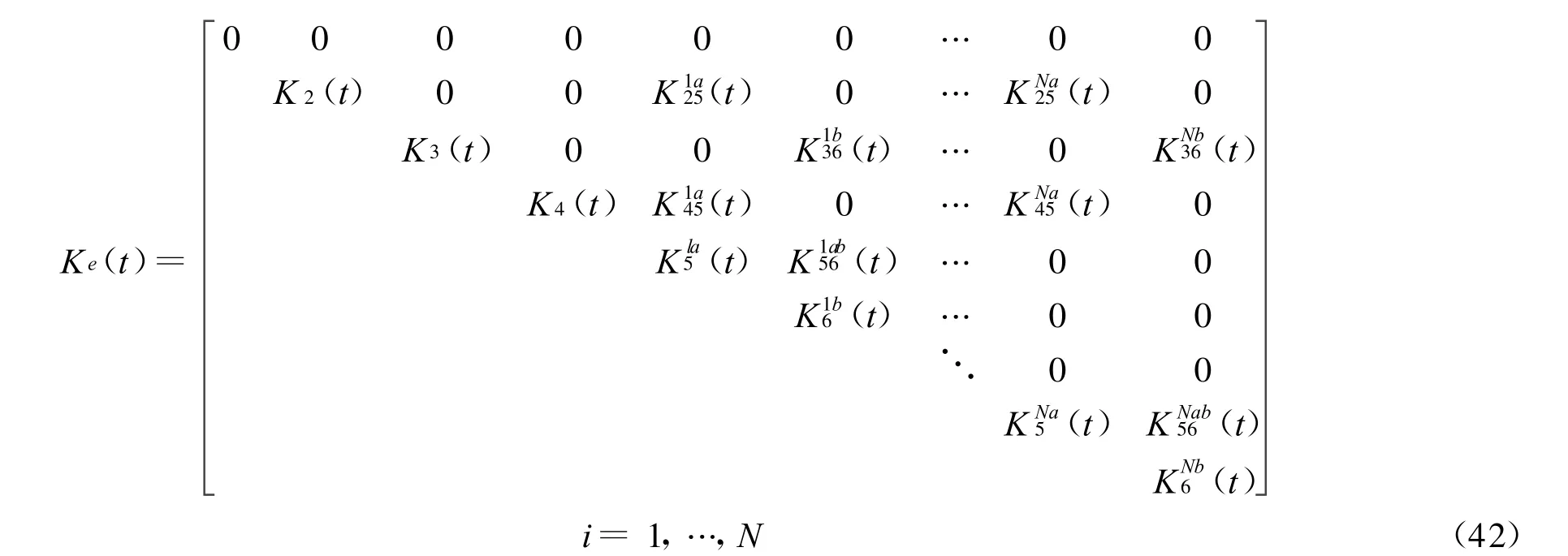
式中

式中

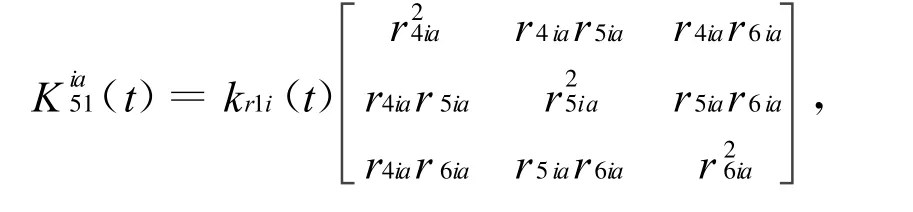
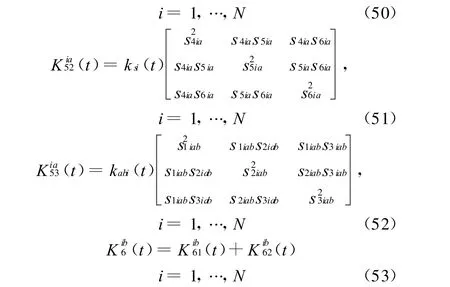
式中

外加转矩矢量为