基于信息熵的建设项目全生命周期确定

□文/侯小斌

一、熵概念

“熵”一词源自希腊语“变化”，表示变化的容量。1824年，为了讨论热机效率，萨迪卡诺提出了有名的卡诺循环；1856年，为了将热力学第二定律格式化，德国物理学家克劳修斯在《热之唯动说》一书中引入熵的概念，创立了熵。申农把信息量作为信息论的中心概念，给出了信息熵公式：

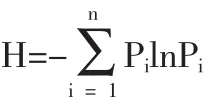
其中，H为信息源，即事件整体的信息源；Pi是事件的概率分布。由于0≤Pi≤1，在此范围内的对数是负值，所以公式在求和符号“∑”之前加负号，这样H永远是非负的。

熵与信息紧密联系，熵是一个系统失去了信息的度量，系统有序性越高，熵越小，此时含的信息量越大；相反，系统越混乱，有序度差，熵越大，含的信息量越小。

二、基于信息熵的建筑工程全生命周期工期确定

1、邀请专家针对建设单位计划建设项目全生命周期每阶段完成的时间进行概率估计。

2、对各专家估计的全生命周期每阶段完成时间的概率进行熵值计算。由于熵值越大，即在信息量最少的情况下，不确定性最高，也是最容易发生事件，即出现的概率也越大。

3、根据熵值最大的估计值，计算建筑工程全生命周期完成所需时间：

T＝t1÷p1＋t2÷p2＋t3÷p3＋t4÷p4＋……

其中，T是全生命周期完成所需工期，t是全生命周期每阶段完成所需时间，p是每阶段完成可能的概率。

三、案例分析

已知某建筑工程全生命周期各阶段任务包括：项目建议书、项目可行性研究、项目初步设计、项目施工图设计、项目招投标、项目施工、项目竣工验收，建设单位根据以往经验，对本工程全生命周期每个阶段需要时间进行了估计，要求在计划工期36个月内完成；并邀请三位专家分别对生命周期内每个阶段的完成时间概率进行估计，如表1所示。（表1）

根据信息熵公式分别计算出三个信息系统的熵值，如下：

表1 项目全生命周期每阶段完成时间估计

H1＝-（0.9×ln0.9+0.9×ln0.9+0.8×ln0.8+1×ln1+1×ln1+0.75×ln0.75+0.95×ln0.95）=0.633

H2＝-（0.8×ln0.8+0.9×ln0.9+0.9×ln0.9+0.9×ln0.9+1×ln1+0.8×ln0.8+0.9×ln0.9）=0.736

H3＝-（0.9×ln0.9+0.95×ln0.95+0.85×ln0.85+0.85×ln0.85+0.9×ln0.9+0.9×ln0.9+1×ln1）=0.609

通过分析比较，可以看出：H3＜H1＜H2，由于熵值越大，即在信息量最少的情况下，不确定性最高，也是最容易发生事件；因此专家2估计的某建筑工程全生命周期所需时间出现的概率比较大。

利用全生命周期完成所需时间公式计算可得，某建筑工程全生命周期完成所需时间：

T＝2÷0.8＋3÷0.9＋5÷0.9＋6÷0.9＋3÷1+15÷0.8+2÷0.9＝42 个月

四、结语

由于建筑工程的单一性、复杂性，以及项目实施过程中存在着大量不可预见的风险因素，致使无法对建设项目全生命周期完成所需时间进行准确估计，从而导致项目建设过程出现工期无法按计划目标完成，项目投资超出计划目标。本文利用信息熵原理，对所收集的专家估计样本进行有效的熵值计算，由于熵值越大，即在信息量最少的情况下，不确定性最高，也最容易发生事件，即出现的概率比较大；最终以熵值最大的专家估计概率来确定建筑工程的全生命周期。

[1]黄崇福.自然灾害风险评价理论与实践[M].北京：科学出版社，2004.

[2]朱亮亮.基于信息熵扩散技术的网络计划工期研究.合作经济与科技，2009.