平面度误差可视化评定系统研究
2011-07-03万文
万 文
(南昌航空大学 航空制造工程学院,南昌 330063)
0 引言
平面是构成机械零件的重要几何要素,它常常被作为检测的基准面,因此对平面度误差进行有效和准确的评定具有重要的实际意义[1]。平面度误差的评定方法较多,常用的有最小二乘法、对角线平面法、三远点平面法和最小包容区域法。目前对于平面度误差评定主要有两大类方法,最小二乘法和最小区域法。前者具有数学理论成熟、方法简单、计算迅速、结果稳定、对误差具有平均作用、测量准确度也较高等特点,本文基于虚拟仪器技术,应用LabVIEW8.5及C语言,针对平面度误差中最小二乘法进行实例编程验证,实现从数据采集到误差分析的一整套功能。
1 最小二乘法误差评定原理
最小二乘法是以最小二乘平面作为评定基准的方法,如图1所示,设被测平面上任一点的坐标值为Pij(Xi, Yj, Zij),理想平面的方程为:=aX+bY+c,按最小二乘法的基本思想,由测量点拟合的该理想平面应使测量点到该平面的坐标值的平方和最小:

对a、b、c 求偏微商,再使偏微商等于零,得到a、b、c应满足式(1)。

图1 平面度误差测量原理图

式(1)化简得:

式(2)用矩阵表示如下:

式(3)通过线性代数即可求出a、b、c,即确定了理想平面的位置,再将各测点相应的坐标Pij(Xi, Yj, Zij)代入平面方程,即可得对应的方向坐标值,所以平面度误差为:

其最大值与最小值之差即为直线度误差f。通过LabVIEW中求最大最小值函数可实现。
最小二乘平面的a、b、c可利用LabVIEW中公式节点,采用C语言编程实现,设a1代表ΣX,b1为 ΣY,c1为 ΣXi,d 为 ΣYi,e 为 ΣXiYi,f为ΣXiZi,g 为 ΣYiZi,h 为 ΣZi,程序如下:
int i;
float a1=0.0,b1=0.0,c1=0.0,d=0.0,e=0.0;
float f=0.0,g=0.0,h=0.0;
for(i=0;i<n;i++)
{a1=a1+x[i]*x[i];
b1=b1+y[i]*y[i];
c1=c1+x[i];
d=d+y[i];
e=e+x[i]*y[i];
f=f+x[i]*z[i];
g=g+y[i]*z[i];
h=h+z[i];}
如图2所示,通过创建数组函数、重排数组函数得到式(3)中的前两个矩阵,对其中3×3矩阵进行逆矩阵转化,可求出a、b、c,即得到最小二乘平面方程,再通过平面上任一点的坐标值与对应的最小二乘平面的Z值相减Zij- (aXi+bYj+c),得到一数组,将该数组中的最大值与最小值相减,得出平面度误差。
2 实例编程
系统平台由电感式测微仪、PCI-6221数据采集卡及PC机等组成。通过采集程序保存数据,实测数据以电子表格的形式保存。可改变采样的直线数和每条直线上的采样点数,本例在采集平面均布4条直线,采用网格布点法,横向4个点,纵向取4个点,采样点数16,通过数据分析程序读出数据,数据分析前面板如图3所示,图中显示4条直线的波形图。误差分析程序可以快速准确得出三维曲面图、最小二乘平面方程、采样点偏差值Z和平面度误差,得到的结果如图4所示,采样点的测量数据如表1所示,评定的误差结果为0.15635mm,最小二乘平面方程为
Z=-0.02162X+0.0054Y+0.44699
3 结束语
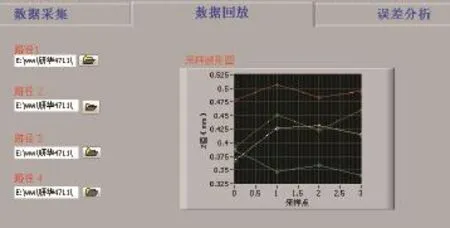
图3 数据回放前面板
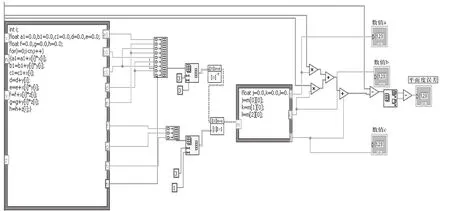
图2 最小二乘法评定平面度误差框图程序
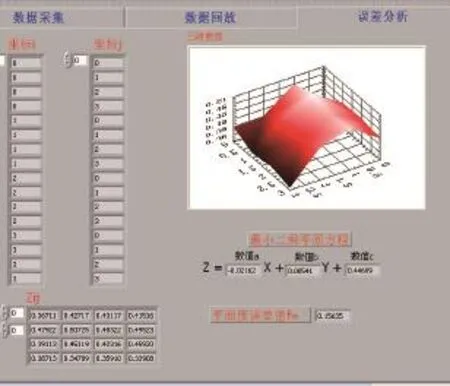
图4 误差分析前面板
用最小二乘法进行平面度误差评定,可以快速准确地完成采集、保存和误差分析,并给出三维曲面图及平面度误差值,开发的系统界面友好,实现了测试过程的自动化、数字化、可视化,提高了平面度误差测试效率、数据处理速度和测试精度。
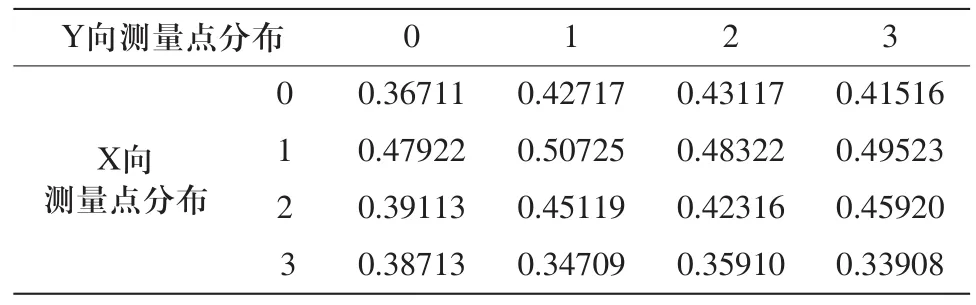
表1 采样点偏差值Z(mm)
[1] 田社平, 韦红雨, 王志武. 用遗传算法准确评定平面度误差评价[J]. 计量技术, 2007, (1): 66-69.
[2] 续永刚, 向立明, 高国生. 零件直线度误差虚拟检测系统研究 [J]. 制造业自动化, 2010, (7): 100-103.
[3] 黄松岭, 吴静. 虚拟仪器设计基础教程[M]. 北京: 清华大学出版社, 2008.
[4] 申焱华, 等. LabVIEW入门与提高范例教程[M]. 北京: 中国铁道出版社, 2006.
[5] 胡仁喜, 王恒海, 齐东明, 等. LabVIEW8.2.1虚拟仪器实例指导教程[M]. 北京: 机械工业出版社, 2008.
