基于CFX的喷嘴喷针流道的水力优化

郑发平，宋文武，冯凌寒，程 飞

（1. 西昌学院工程技术学院，四川 西昌 615013；2. 西华大学能源与环境学院，成都 610039）

1 引言

我国是一个水力资源相当丰富的国家，水能又是清洁可再生能源，开发水能是实现可持续发展战略的重要条件。但我国水力资源又相差很大，特别是西南地区多山区河流，这些河流的特点就是水头高，流量小，因而，冲击式水轮机有着很大的发展前途，该机型的特点是结构简单、造价较低，在较大的流量出力范围内具有较高的效率。目前，我国冲击式水轮机发展水平还较低，特别是高水头、大容量、多喷嘴形式的冲击式水轮机与国外先进水平相比还有较大距离。喷嘴及喷针的几何流道不仅影响喷嘴内部流场，而且也会影响射流情况和能量的转换。因此，喷嘴几何流道对水轮机的影响是不可忽视的，对其进行研究对水轮机的性能有着极其重要的意义。

2 数值模拟

2.1 研究对象

本文结合传统的三种喷嘴流道进行数值分析比较，并自行开发设计了两种喷嘴与喷针流道几何型线，以达到喷嘴几何流道优化的目的。

研究对象相关参数如表1所示。

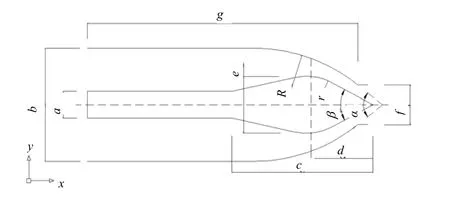
图1 喷嘴流道几何简图

表1 喷嘴喷针流道主要参数

2.2 控制方程

牛顿流体非定常流动控制方程的雷诺时均形式如下：

连续性方程

动量方程

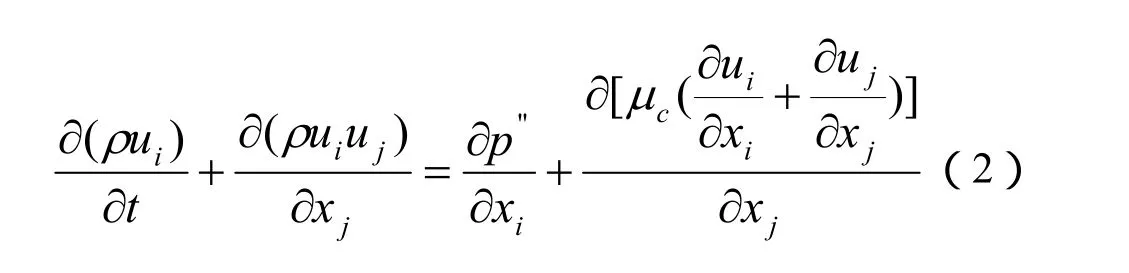
式中： ui——平均速度；

cµ——有效粘性系数，表示分子粘性系数µ与湍流涡粘性系数之和。

本次非定常计算采用标准的k-ε湍流模型：

方程（3）、（4）中，Gk表示由层流速度梯度而产生的湍流动能，Gb是由浮力产生的湍流动能，YM代表可压湍流中脉动扩张的贡献，Sk和Sε表示用户自定义的源条件。

2.3 数值模拟

为了更好地比较各流道，设计流场出口直径均为122.8mm。在WORKBENCH中，进行建模并进行网格划分，计算区域和网格划分如图2所示。

2.4 边界条件

设置进口速度为9m/s，出口相对压力为0。在求解控制器中设置 Timescale Control为 Physical Timescale，设置Physical Timescale 为0.01[s]。

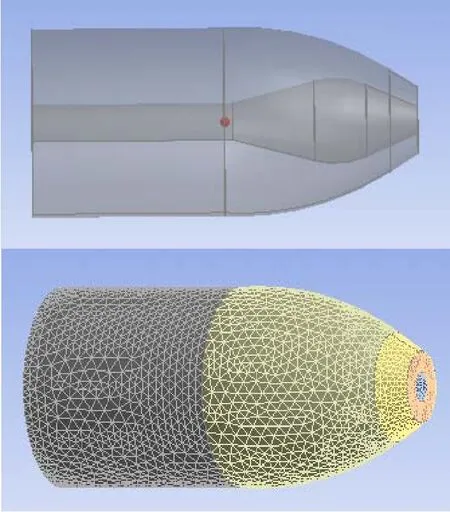
图2 流场模型及网格划分

3 计算结果及分析

3.1 流场计算结果比较分析

对模型进行CFX数值模拟后，对结果进行分析由能量方程V2/2g+P/γ+z=c进行校核。设△E为进出口的能量变化，5种方案的能量变化比较结果如下表：

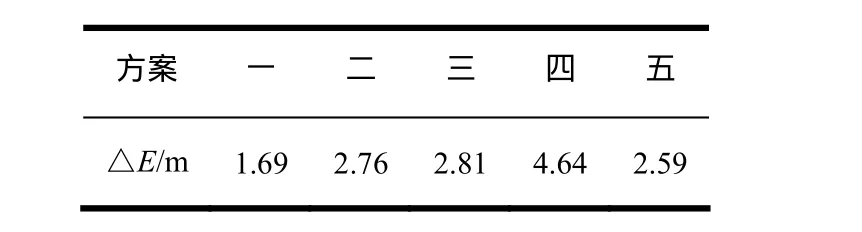
表2 进出口能量变化

5种方案中，方案一的损失最小，从能量损失来看，此为最优方案，而方案四的损失最大，将不再对方案四继续分析。将方案二，方案三，方案五进行比较，找出较优的两种方案与方案一构成较优的三种方案，达到优化三种传统方案的目的。

图3中，(a)，(b)，(c)分别为方案二，方案三和方案五的出口压力，速度和流线分布图。模拟进口速度均设置为9m/s，通过CFX模拟计算得到三种方案的出口平均速度，方案二为91.9m/s，方案三为105.3m/s，方案五为95.7m/s。

3.2 结论

通过运用CFX软件，将不同尺寸的流道进行了数值模拟分析及比较，可以得出传统的三种方案中，从能量变化上看，方案一是最优的，而方案二和三的损失接近，为得到较优的三种方案，比较结合出口参数分布云图和流线分布可以得出，方案二（图3a）参数分布较差，有明显的梯度变化，而方案三（图3b），方案五（图3c）的分布比较均匀。在相同的速度进口下，方案五的出口速度也高于方案二，这也说明了方案五的能量损失较小。从加工制造和经济性角度考虑，图1和表1所示，方案五的喷管直径b较方案二的小，方案五喷管过度圆弧半径R和喷嘴过度圆弧半径r都比方案二的大，喷管直径b较小节约了材料，过度圆弧半径较大降低了加工难度。综上所述，传统的三种方案中的方案二应该被方案五替代，从而优化了传统方案。

图3 出口压力、速度及流线分布计算结果

[1]李贵斌, 等. 冲击式水轮机喷嘴射流的CFD技术[J]. 水电能源科学, 2003, 21（1）：72-79.

[2]机械工程手册编辑委员会, 电机工程手册编辑委员会.机械工程手册[M].北京：机械工业出版社,1982.

[3]程良骏. 水轮机[M]. 北京：机械工业出版社,1984.

[4]H. K. Versteeg, W. Malalasekera. An Introduction to Computational Fluid Dynamics [M]. The Finite Volume Method. Wiley, New York, 1995.

[5]王福军. 计算流体动力学分析[M]. 北京：清华大学出版社.2004.

[6]H. Schlichting. Boundary Layer Theory [M], 8thed.McGrawHill, New York, 1979.

[7]S. V. Patanker, D. B. Spalding, A calculation processure for heat mass and momentum transfer in three-dimensional parabolic flows [J]. Int J Heat Mass Transfer, 15:1787-1806, 1972.