双PMW直驱同步风力发电的低电压穿越控制

刘胜文，包广清，范少伟，刘 峻 ，李正元

（1.兰州理工大学 电气工程与信息工程学院，兰州730050；2.甘肃电力科学研究院，兰州 730050）

引言

风力能源是理想的清洁能源，目前我国近海风场的可开发风能资源是陆上实际可开发风能资源储量的3倍，接近7.59亿kW[1]。但海上风电是陆上风电的2倍，为降低成本，海上风电场需要更大的风力发电单机容量、更少的维护成本以及更可靠的风力发电机组。直驱永磁同步风力发电机（PMSG）直接与风力机相连接，转速低，极数多，定转子尺寸大，呈扁平状结构，具有转动惯量大的特点，PMSG的这些特性有利于抑制风力起伏引起的电势波动，同时PMSG无齿轮箱，对电网有更好的融合性[2-4]，以上特点使得PMSG应用在海上风电有明显的优势。由文献[5]可知，为实现风电并网，风电场内风力发电机组应具有在并网点电压跌至20%额定电压时，能够维持并网运行0.625s的低电压穿越能力（LVRT）。

电网电压跌落时往往会使直流母线电压过高，目前PMSG系统的LVRT采取的主要措施有[6]：①选择耐压和过流值比较大的电力电子器件，并提高直流电容的额定电压值；②增加辅助网侧变流器；③在直流母线（DC-link）上接储能系统或Buck变换器；④采取变桨控制。其中措施①～③需要改变或增加器件，增加了系统的成本，措施④的动态响应比较慢。因此，本文提出一种基于功率变换的控制方法，通过机侧整流器稳定直流母线电压，网侧逆变器跟踪风力机的转速实现最大风能利用。电网跌落时，使系统输入和输出不平衡的能量转化为风力机和发电机的动能，从而提高低电压穿越能力，保证系统安全度过电网故障。

1 风力机模型

双脉宽调制(PWM)变换器因具有功率双向流动等特点，并且具有优良的运行特性,因而在风力发电技术研究中得到了广泛关注[7]。本文采用图1所示的PMSG系统，图中C为直流母线（DC-link）电容，idcDC-link电流，udc为DC-link的电压，R为电抗器及开关管的等效电阻，L为网侧电抗的电感。

图1 直驱式永磁同步风力发电系统

风力机数学模型为[8]：

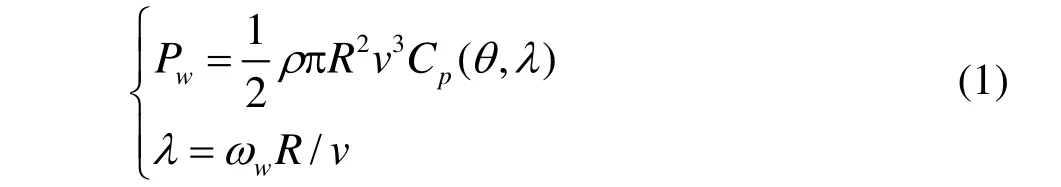
式中：Pw为轴机械功率；λ为叶尖速比；ρ为空气密度；R为风叶半径；wω为风力机转速；v为风速；Cp为风能利用系数。

风能利用系数定义为：

当桨距角θ=0o时，风力机的风能利用系数为最大值= 0 .44，而叶尖速比为= 6 .9。对于桨距角固定但风速不同的情况下，风力机的输出功率P曲线如图2所示。

图2 风力机功率特性

由图2可知，对每个风速都存在一个特定的转速，使得风力机的输出功率最大。则当P小于额定功率时，P和转子速度参考值则存在如下关系[9]：

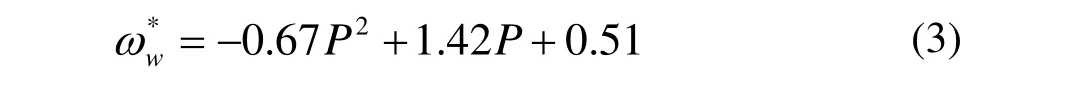
2 控制策略

忽略发电系统的功率损失，风机转速、直流母线电压和系统各有功功率之间的关系可以表示为：

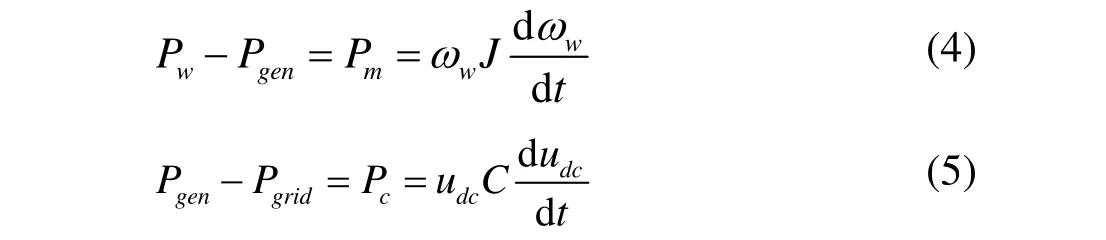
式中：Pm为转变成风力机和发电机动能的功率；cP为贮存在DC-link上电容C功率；Pgrid为注入电网中的有功功率。

在传统的控制方法里[10]，机侧整流器用来控制发电机输出功率，跟踪最佳的转速参考值；网侧逆变器用来保持的DC-link电压和向电网输出有功和无功。当电网电压跌落时，由于电流不能突变，Pgrid迅速变小。然而机侧整流器仍保持PMSG的最大功率输出，Pgen基本不变；与此同时网侧逆变器为了传送等量的有功，需增大输出电流，而流过逆变器的最大电流值由参考的限幅值决定，使输出功率增加受到限制。根据式（5），在电压跌落时，将会有更多的能量储存在DC-link的电容上，这必然导致udc升高，这会对变流器造成损坏。

为此，本文引入一种基于功率变换的控制方法，控制结构如图3所示，图中gθ为转子位置角；Ld、Lq分别为发电机在d、q轴下的电感；ugd、ugq分别为定子电压的d、q分量；igd、igq分别为定子电流的d、q分量；eω为发电机电角速度；ψf为永磁体磁链；usd和usq为逆变器的d、q轴电压分量；isd和isq为逆变器的d、q轴电流分量；esd和esq为电网电压的d、q轴分量；gω为电网角频率。

在图3所示的控制系统中，机侧整流器的目的是维持电压udc的值保持在一定的范围；网侧逆变器的目标是能根据风能捕获原则输出最佳功率。机侧整流器是采用电流igd为内环、电压udc为外环的双闭环控制结构。以DC-link的额定电压为电压参考值，实际的udc为负反馈，经PI调节得到。网侧逆变器也采用双闭环控制结构。由电网电压和电流得到系统所要输出的有功功率，利用式（3）最大风能跟踪原则中功率与风机参考转速的关系，得到转速参考值，但当转速高于或等于1p.u.时，为1。从而使系统能根据注入电网有功功率的需求，使发电机运行在最佳转速，实现最大风能跟踪。

式中Q为电网需要的无功功率；i为逆变器允许流过的最大电流值。

图3 新的控制结构

当系统联结点的电压跌落时，直流母线两侧输入功率大于输出功率。为了保持直流母线上电压为常数，由于udc的负反馈，机侧整流器将减小电流igd来减小发电机输出功率，由式（5）可知udc将得到有效的抑制。但如果系统不采用变桨控制，Pm基本不变，由式（4）可知，这将会使得风力机的转速升高，然而对于MW级的风力发电机来说，转速的提升是比常小的。

3 仿真与分析

本文针对图1所示容量为2MW的直驱式永磁同步风力发电系统，在 MATLAB/SIMULINK仿真环境下，对传统控制方法和本文提出的控制方法进行对比分析。假定风速为11m/s，图4所示的是在0.02s-0.72s并网点电压跌落至 15%时（图 4a），在传统的控制方法和新的控制方法下，系统的LRVT能力。

仿真参数如下：

（1）风力机：空气密度1.225kg/m3，风轮半径40m，额定风速11m/s；

（2）PMSG：极对数 40，定子线电压 730V，机组转动惯量 4.32，磁感应强度 1.2pu，定子相电阻为0.006pu，交轴电感 Xd为 1.305p.u.，直轴电感 Xq为0.474p.u.，额定转速2.5rad/s；

（3）变流器：直流电容0.2F，直流电压1100V，开关频率 2kHz，输出额定电压 690V，输出的限定电流1.1p.u.，无功设定值0，电网角频率50Hz。

当电网电压跌落时，系统的输出功率迅速减小，如图4b。为了保持DC-link上电压为一定值，机侧整流器将减小电流igd来减小发电机输出功率，从图4e中可以看到，在新的控制方法下，发电机的输出功率迅速变小了，由图4c可知，DC-link上电压udc在一个比较小的范围内变化，上升的幅值比在传统控制方法下的小很多。然而由式（4）可知，由于功率不平衡，会使一部的能量存储在风力机上，这样风力机的转速wω提升了一些，上升的幅度在0.08内，在安全范围内，如图4d。由于无功功率的控制在本文的控制和传统的控制方法一样，为了调节并网点电压，无功功率输出基本上没有变化，如图4f。

图4 电网电压骤降下传统的和新的控制的仿真对比

4 结论

本文在传统功率变换器控制方法的基础上，提出一种基于功率变换的控制策略，通过发电机侧整流器来调节直流母线电压，而网侧逆变器则用来从风能中跟踪最大的功率。仿真结果表明，当电网故障引起电压的大幅跌落时，本文提出的控制方法能有效地减小直流母线上的电压上升，从而提高其低电压穿越的能力，保证风电系统能安全有效地度过电网故障。但由于PMSG的转子没有阻尼绕组和励磁绕组，发电机的转速波动较大，需引入阻尼控制抵制波动，这有待进一步研究。

[1]李俊峰, 施鹏飞, 高虎. 中国风电发展报告2010[M]. 海口:海南出版社, 2010.

[2]关宏亮, 赵海翔, 王伟胜. 风电机组低电压穿越功能及其应用[J]. 电工技术学报, 2007, 22(10):173-177.

[3]Ge Jun，Tong Luyuan，Geng Juncheng，et al.Research on thyristor conduction angle characteristics in transient process of TCSC[J].Power System Technology, 2001, 25(7):18-22.

[4]范高锋, 赵海翔. 大规模风电对电力系统的影响和应对策略[J]. 电网与清洁能源, 2008, 24(1):44-47.

[5]张兴, 等. 风力发电低电压穿越技术综述[J]. 电力系统及其自动化学报, 2008, 20(2): 1-8.

[6]Carrasco J M , Franquelo L G, Bialasiewicz J T,Power-electronic systems for the grid integration renewable energy sources: A survey [J]. IEEE Transactions on Industrial Electronics, 2006, 53(4):1002-1016.

[7]宋卓彦, 王锡凡, 滕予非, 等. 变速恒频风力发电机组控制技术综述[J]. 电力系统自动化. 2010,34(10): 8-17.

[8]姚骏, 廖勇, 庄凯. 永磁直驱风电机组的双 PWM变换器协调控制策略[J]. 电力系统自动化. 2008,32(20): 88-107.

[9]Slootweg J.G., de Haan S.W.H., Polinder H..General model for representing variable speed wind turbines in power system dynamics simulations[J].IEEE Trans. Power System, 2003, 18(1): 144–151.

[10]Nicholas W. Miller, Juan J., Sanchez-Gasca.Dynamic modeling of GE 1.5 and 3.6 MW wind turbine generators for stability simulations[C].IEEE WTG Modeling Panel Session, July 2003.