基于模糊控制的车辆侧倾稳定性联合仿真
2011-06-29朱茂桃秦少隽
陈 阳,朱茂桃,秦少隽
(1.上海大众产品工程部,上海201805;2.江苏大学 汽车与交通工程学院,江苏 镇江212013)
随着汽车技术的不断发展,车辆的安全性和操纵稳定性越来越受到重视。汽车在高速行驶或在低附着系数路面上行驶时,由于受到外界干扰或驾驶员转向作用,侧向附着力常常达到附着极限,使车辆侧倾稳定性变差,容易造成交通事故。因此,提高车辆的侧倾稳定性对行驶安全意义重大[1]。
笔者选用某型号的越野车为研究对象,在ADAMS/Car模块中建立整车系统动力学模型,利用MATLAB建立模糊控制控制器模型,将控制器与整车模型相结合对横摆角速度和质心侧偏角进行联合控制仿真[2]。
1 整车系统动力学模型
1.1 整车模型的建立
研究的越野车为后置后驱式,前悬架为螺旋弹簧非独立悬架,后悬架采用的是纵置钢板弹簧非独立悬架。在ADAMS/Car中建立的整车模型如图1。
1)前悬架:主要由上下横臂、主销轴、转向横拉杆、螺旋弹簧和减震器等组成。
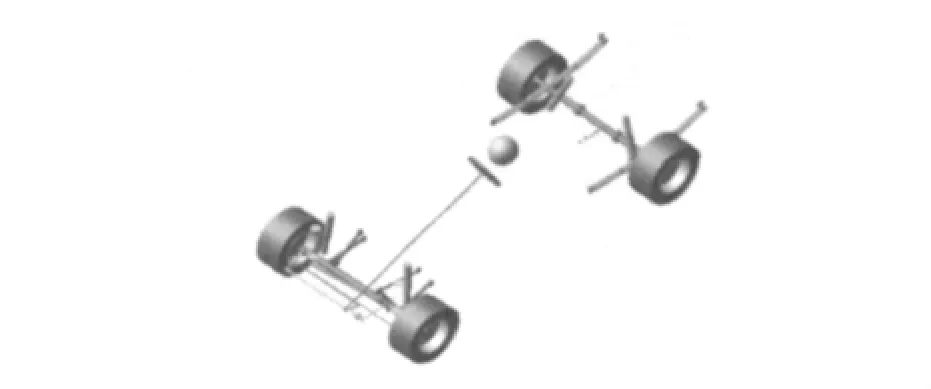
图1 整车虚拟样机模型Fig.1 Virtual prototype model of vehicle
2)后悬架:主要是由纵置单片钢板弹簧,整体桥,减振器组成。建模时,钢板弹簧简化为非线性多义梁(Nonlinear Beam)。
3)转向系统:采用拉杆式转向器。
4)横向稳定杆:采用2根断开轴中间通过转动副连接,并在转动铰链上施加扭转力进行简化建模。
5)轮胎:前后轮胎均采用Fiala轮胎模型。将轮辋简化成刚性圆板,胎体由支撑于圆板上的弹簧表示,胎冠则简化圆环梁并由弹簧支承[3]。
6)动力总成:采用后置发动机,将发动机、变速器、离合器集合成一体,用函数模拟实现各部分的功能。
7)制动系统:采用4通道盘式制动控制。
1.2 模型的验证
对比实车试验和模型仿真来验证虚拟样机模型的正确性。试验为双移线试验和蛇形试验,均在定远专用试验场地进行实车试验。
1.2.1 蛇形试验
蛇形试验按照国家标准GB/T 6323.1—94《汽车操纵稳定性试验方法蛇形试验》[4]的要求进行。初始车速50 km/h,总共10个桩,L=30 m。实验与仿真结果如图2、图3。

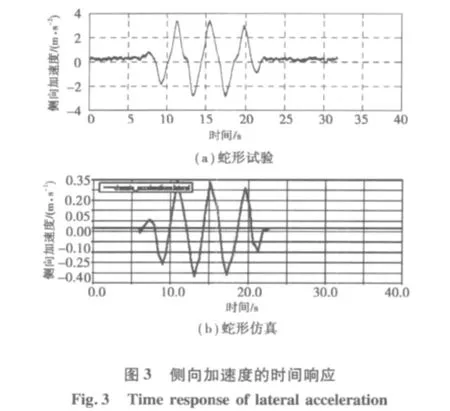
1.2.2 双移线试验
初始车速60 km/h,试验过程中采集到的数据和试验仿真数据如图4、图5。
从上述试验及相应工况下仿真试验的比较,发现表征车辆侧向稳定性的2个变量横摆角速度和侧向加速度的试验值与仿真值均能较好的保持一致,验证了虚拟样机模型的正确性,为车辆侧倾稳定性控制的研究提供了可靠的理论模型。


2 模糊控制器的设计
2.1 以横摆角速度为控制变量设计控制器
对横摆角速度进行控制时,采用二维模糊控制器,输入变量为实际横摆角速度r与理想横摆角速度rd的偏差e(r),以及偏差变化的快慢ec(r),输出变量u为横摆力矩MZ(r)。
变量误差e(r)、误差变化ec(r)及控制量u的模糊集如下:
e(r)的模糊集均为:{NB,NM,NS,PO,PS,PM,PB}
式中:NB为负大;NM为负中;NS为负小;PO为正0;PS为正小;PM为正中;PB为正大。
所取的控制力矩的原则,是当误差大或较大时,所选的控制横摆力矩以尽快消除误差为主;而当误差较小时,选择控制横摆力矩要注意防止超调,以系统的稳定性为主要出发点。根据这种原则列出控制规则见表1。

表1 模糊控制规则Tab.1 Fuzzy control rules
以横摆角速度为控制变量的控制器的输入输出关系,如图6。

图6 模糊控制器的输入、输出关系Fig.6 Relations of fuzzy controller’s input and output
2.2 以质心侧偏角为控制变量设计控制器
对质心侧偏角进行控制时,仍用二维模糊控制器,输入变量就变成实际质心侧偏角β与理想横摆角速度βb的偏差 ec(β),以及偏差变化的快慢 ec(β),输出变量u为横摆力矩MZ(β)。它们的定义范围和横摆角速度的控制是一样的,不同的是模糊控制规则的设定。基于质心侧偏角反馈控制的模糊规则表,如表2。模糊控制器的输入输出关系见图7。

表2 模糊控制规则Tab.2 Fuzzy control rules
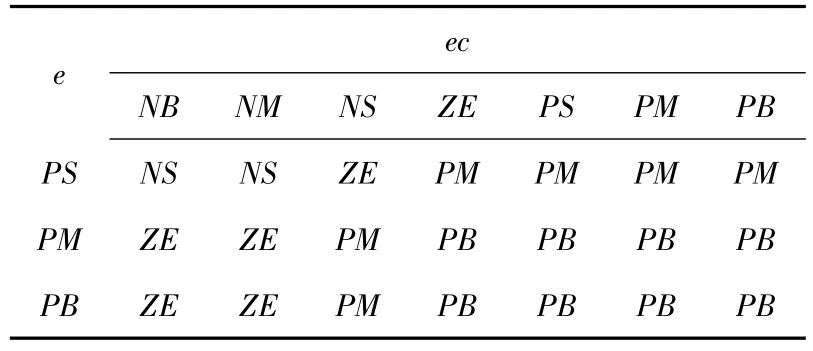
(续表2)
2.3 以横摆角速度和质心侧偏角为控制变量设计控制器
横摆角速度和质心侧偏角联合控制时,输入变量为横摆角速度的偏差e(r)和质心侧偏角的偏差e(β),输出变量为横摆力矩MZ。
联合反馈控制的输出变量是经过加权并相加后得到的总的横摆力矩[5-6]。即:
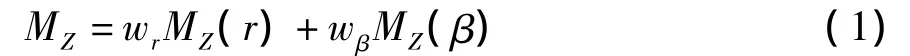
式中:MZ为控制器输出的总的横摆力矩;MZ(r),wr分别为横摆角速度控制器输出及加权因子;MZ(β),wβ分别为质心侧偏角控制器输出及加权因子。
3 联合仿真计算和结果分析
3.1 建立联合仿真模型
进行仿真前需要专家模块定义输入输出变量,实现ADAMS和控制程序之间的闭环控制。ADAMS的输入变量是四轮制动力矩变量,输出变量是车身侧向加速度、车身质心侧偏角、车身纵向车速、车身横向车速、车身横摆角度、汽车行驶车速。然后建立操纵稳定性仿真的控制文件,根据车辆试验时测力转向盘记录的数据输入,以保证仿真的真实性。
在MATLAB/Simulink里面建立整车操纵稳定性的二自由度模型,并采用单轮制动产生附加横摆力矩来控制汽车在极限情况下的横摆角速度和质心侧偏角。
联合仿真之前应该将 adams_server.py、decode.m和adams_plant.dll三个文件放在ADAMS工作目录下,否则仿真的时候MATLAB与ADAMS无法建立连接。在Controls下的Plant Export中将输入输出变量填入到对话框内,点击后自动生成(.m)文件。在ADAMS/Car中Simulate下的File Drive Events输入路面文件和控制文件,单击后自动生成ADAMS Solver数据文件(.adm)、驾驶员控制文件(.dcf)和Solver控制文件(.acf)等。修改(.m)文件,使控制的文件与之对应。打开MATLAB,修改工作路径使之与ADAMS的相同,输入相应的命令打开生成的(.m)文件,再输入 adams_sys,调出 adams_sub,然后与MATLAB建立的横摆角速度控制系统模型连接起来[7-8]。同理,将导入 MATLAB的整车模型与建立的质心侧偏角控制器相连接,建立基于质心侧偏角反馈控制的联合仿真图。
将两者结合起来,建立横摆角速度和质心侧偏角联合反馈控制的联合仿真图(图8)。
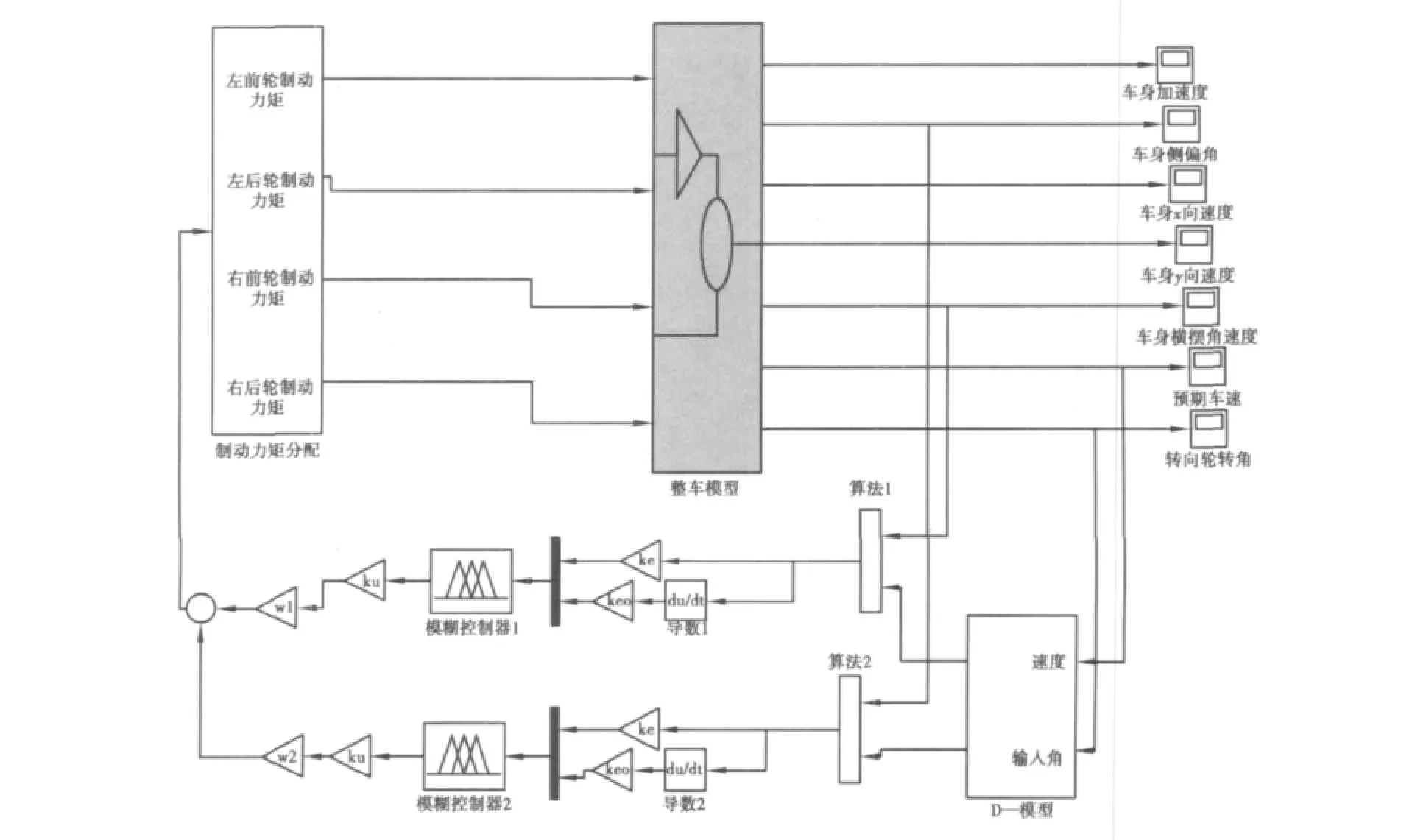
图8 联合仿真系统结构Fig.8 Structure of co -simulation model
3.2 仿真分析和仿真结果
3.2.1 单正弦输入仿真与分析
单正弦转向行驶,即汽车变路径行驶。仿真条件为前轮转向角为单正弦输入,汽车的初始车速为110 km/h,地面附着系数为1,即汽车高速时转向的极限工况下的仿真。频率为0.5 Hz,幅值为100°,约1.75 rad。仿真结果如图9、图10。

图9 不同反馈控制的横摆角速度响应对比Fig.9 Yaw velocity response of different feedback control

图10 不同反馈控制的质心侧偏角响应对比Fig.10 Sideslip angle response of centroid of different feedback control
3.2.2 角阶跃输入仿真与分析
驾驶员对转向盘进行阶跃输入,常用转向盘角阶跃输入下的瞬态响应来表征汽车的操纵稳定性。仿真条件:前轮转向角阶跃输入,汽车的初始车速为50 km/h,地面附着系数为0.2,即汽车在地附着湿滑路面上进行圆周行驶的极限工况,最大的输入角为100°。仿真结果如图11、图12。
从2个实验中横摆角速度响应和质心侧偏角响应对比图中可以明显看出,无控制情况下,汽车的横摆角速度和质心侧偏角都远远大于理想情况。


4 结论
本文基于ADAMS/Car建立整车虚拟样机模型,并通过实验验证了模型的正确性。基于模糊控制理论设计了横摆角速度反馈模糊控制器、质心侧偏角反馈模糊控制器以及这两个变量联合反馈的模糊控制器。在模糊理论的基础上建立联合仿真模型,进行了转向盘单正弦输入和在转向盘角阶跃输入的操纵稳定性仿真,比较分析了横摆角速度反馈控制器、质心侧偏角反馈控制器,以及联合反馈控制器的控制效果。结果表明:3种控制方法都可以较好的控制汽车的横摆角速度,提高了汽车行驶时的稳定性。采用2个变量联合反馈控制的控制效果优于单个变量的反馈控制,并且横摆角速度反馈控制器优于质心侧偏角反馈控制器。
[1]李白娜.汽车操纵稳定性的仿真分析研究[D].武汉:华中科技大学,2006.
[2]范成建,熊光明,周明飞.虚拟样机软件MSC.ADAMS应用与提高[M].北京:机械工业出版社,2006.
[3]陈军.MSC.ADAMS技术与工程分析实例[M].北京:中国水利水电出版社,2008:161-163.
[4]GB/T 6323.1—94汽车操纵稳定性试验方法蛇形试验[S].北京:中国标准出版社,1994.
[5]安丽华.汽车电子稳定性程序ESP可控制方法及联合仿真研究[D].南京:南京理工大学,2009.
[6]马春卉.基于MATLAB的汽车ESP系统控制模型及方法研究[D].南京:南京理工大学,2008.
[7]MSC Software Company.Getting Started Using ADAMS/Controls[M].California:Mscprc Press,2007.
[8]MSC Software Company.ADAMS/Car User`s Guide[M].California:Mscprc Press,2003.
