一种使用离散时间尺度变换技术的合成宽带雷达成像系统✴

魏麟

（中国民航飞行学院航空工程学院，四川广汉618307）

一种使用离散时间尺度变换技术的合成宽带雷达成像系统✴

魏麟

（中国民航飞行学院航空工程学院，四川广汉618307）

基于离散时间尺度变换技术，提出了一种新的适用于合成宽带信号的机载雷达成像系统。为了消除多普勒散布效应，该系统使用了尺度变换矩阵，将同一目标在不同子带上的多普勒频率变换到一个已知的频率上，以便每一个子带可使用相同的传统多普勒滤波器组形式去获得无失真的合成距离像。同时，利用FFT及CZT算法，进一步推导出尺度变换矩阵的一种快速实现算法。实验仿真结果验证了所提方法的有效性。

机载雷达；合成距离像；宽带信号处理；离散时间尺度变换；多普勒滤波器组

1 引言

高分辨距离像不仅能够充分反映出目标径向上后向散射密度的几何结构分布，提供出比低分辨雷达更多的识别特征，而且避免了二维或三维成像过程中复杂的计算问题，是现代雷达目标识别技术的基础［1］。径向距离上的高分辨力意味着所用雷达信号的大带宽，在实际中机载雷达为了克服宽带信号处理中的难题（例如多普勒散布效应等），可采用合成宽带技术来获得目标的一维距离像［2］。

合成宽带技术基本原理是发射和接收一系列不同中心频率的窄带脉冲信号，通过对回波脉冲进行运动补偿及相干合成，得到目标的高分辨合成距离像［3］。例如，步进频率信号就是其中最典型的一种信号形式［4］。

由于各个窄带信号的中心频率不同，难以利用相干脉冲雷达的动目标显示（MTI）及动目标检测（MTD）技术，这使得对严重杂波环境下如何分辨不同速度目标并对其进行成像处理，成为合成宽带技术所遇到的最大挑战之一［5］。文献［6］提出了步进频率信号使用两个同频脉冲一次对消地面杂波方法，文献［7］中提出了一种子带脉冲组串方法，即通过在每一个子带中心频率上发射一组相干脉冲，再通过脉组内传统的多普勒滤波器组来提高信噪比或估计目标速度，最后通过脉组间的相干处理，获得距离维高分辨率的效果。

要消除杂波和干扰，雷达中对相干脉冲串的处理是不可避免的。当利用多个窄带信号的相干脉冲串来合成宽带信号时，研究如何消除各个窄带信号中心频率不同而带来的多普勒散布效应以获得无失真合成距离像的方法是十分有必要的。

本文提出了一种新的合成宽带雷达成像系统，其利用数字信号处理中的离散时间尺度变换技术对各个窄带信号的相干脉冲串进行处理，使其变换到一个已知多普勒频率上，以便使用传统多普勒滤波器组来进行处理。与此同时，文中还进一步推导出所提出变换方法的快速实现算法。仿真结果表明，所提出的成像系统可有效消除多普勒散布效应，从而获得无失真的合成距离像。

2 算法模型及理论分析

2.1 多普勒散布项

图1为一个典型的合成宽带时域处理框图。如图所示，通过频分多路模块后，合成宽带信号被分成多个子带信号，每个子带内使用时域滤波器组处理相干脉冲串信号（例如MTI和MTD），接着，再对滤波器组的输出进行成像处理（考虑到效率和运算速度，可使用IDFT），以便获得合成距离像。为了避免多普勒散布项引起的失真，每一个子带的时域滤波器组不能再使用FFT作为实现方式（而改由不同参数的DFT实现），这将会提高系统硬件复杂度和降低计算效率。

图1 合成宽带距离像时域处理框图Fig.1 Temporal processing block diagram of synthetic wideband range profile

下面，我们来具体分析多普勒散布项及其对合成距离像的影响。合成宽带雷达系统参数设置如下：设有N个子带，第n个子带中心频率为fn=f0+ nΔf（n=0～N-1），其中f0为第1个子带中心频率，各个子带中心频率间隔均匀，大小为Δf，子带带宽ΔB=Δf，系统总带宽B=NΔf。脉冲重复频率及脉冲重复间隔可分别表示为fr和Tr=1／fr。一个相干积累间隔（CPI）内的相干脉冲数设置为M，c表示光速。

当子带带宽满足窄带要求时，径向速度为vt的目标在第n个子带内的多普勒频率为

其中，ant是第n个子带中心频率fn上对目标频域响应的采样值，而f0d=2vtf0／c，Δfd=2vtΔf／c，其中Δfd是由于子带中心频率差而引起的目标多普勒频率差，本文中称之为多普勒散布项。

由式（1）可知，同一径向运动目标在不同子带内会产生不同的多普勒频率值，那么，假如在每一个子带内使用相同的多普勒滤波器组结构，则在不同子带内的同一个滤波器输出会表现为不同的值，这等同于对目标频域响应采样值ant加权，从而造成合成距离像的失真。文献［8］详细分析了传统FFT多普勒滤波器组结构对所合成距离像的影响，指出由于存在多普勒散布项，所合成的距离像存在着幅度变形和位置平移。

2.2 离散时间尺度变换分析

由式（1）可看出，目标时域快拍矢量等同于以脉冲重复周期采样所获得的离散序列。以第p和第q个子带为例，目标时域矢量可表示为以下形式：

显然，此时Spt和Sqt可视为对连续信号s（t）= exp｛j4πvtt／c｝分别使用了采样周期Tsp=Trfp和Tsq=Trfq进行采样而获得的离散序列（这里Tsp和Tsq是无量纲的，因而不是通常意义上的采样周期，但由于上式s（t）中的vtt／c也是无量纲的，获得的离散序列与通常意义上的采样周期所获得的离散序列是一致的，因而不会对后续推导产生影响）。基于此，我们也可等价地认为正是由于N个子带内使用了不同的采样周期，从而造成了式（1）中的多普勒散布项的出现。

由信号理论可知，只要满足采样定理，则离散信号序列可无失真地恢复相应的模拟信号。这给我们提供了这样的思路：先通过离散序列Spt无失真地恢复连续信号s（t），再使用Tsq对s（t）进行采样，即可获得Sqt，这样就可消除由于N个子带内使用了不同采样周期而引起的多普勒散布项。

下面，我们将推导出将第p个子带的目标时域矢量Spt（采样周期为Tp）变换为第q个子带的目标时域矢量Sqt（采样周期为Tq）的具体方法。通过延伸此方法，N个子带的目标时域矢量（N个不同采样周期）可统一变换为一个固定采样周期的目标时域矢量，从而消除多普勒散布项的不利影响。

由数字信号处理理论，可将Spt视为满足采样定理的离散序列，则其频域可表示为（注意，式（2）中的Tsp和f都是无量纲的，不会对后续的推导产生影响）：

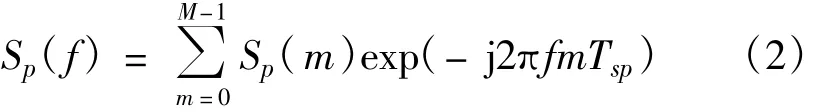
其中，Sp（m）=exp｛j4πvtfpTrm／c｝（m=0～M-1）是Spt中的第m个元素。这样，可通过下式恢复出连续信号s（t）：

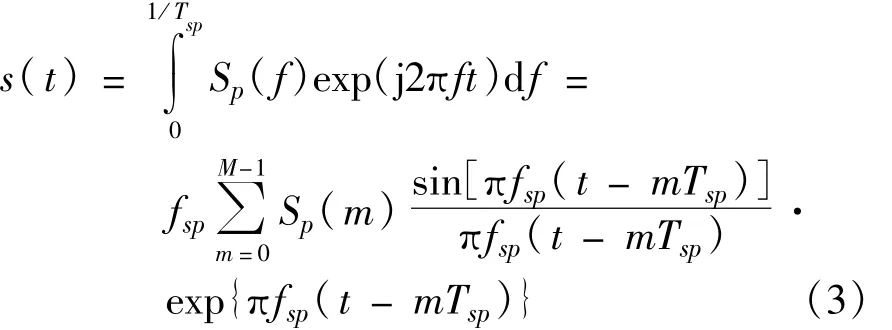
式中，fsp=1／Tsp。显然，假如再使用采样周期Tsq对s（t）进行连续M个采样，即可精确地获得Sqt。Sqt中第r个元素可表示为

由此，可将Spt变换为Sqt，其矩阵形式可表示如下（由于fsp为已知量，对成像处理无影响，故可略去）：

式中，Tpq是M×M矩阵。显然，上述处理的实质是一种离散的时域尺度变换，因此本文中称Tpq为尺度变换矩阵，其元素tr，m的表示式为

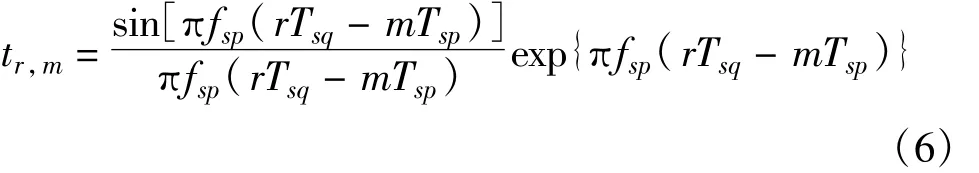
考虑到实际工程的需要，下面我们将基于FFT和CZT算法，推导出式（5）的快速实现算法，以便更高效地实现时间尺度变换。具体推导如下：

当使用频域离散采样值Sp（k）（k=0～M-1）来代替式（2）中的连续量Sp（f）时，s（t）可表示为

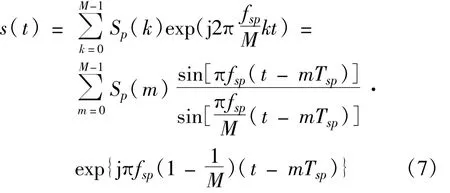
则Sqt中第r个元素可表示为

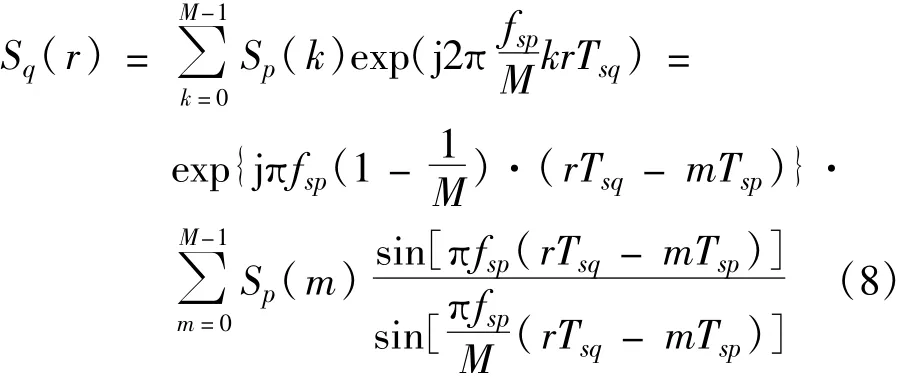
与式（4）相比，上式中指数项中多了（1-1）项。当M M较大时，可近似认为式（8）和式（4）中的s（rTsq）相等。由式（8），则Sqt的矩阵变换形式可表示为

式中，Tfft是FFT变换矩阵。显然，式（9）中TfftSpt表示对矢量Spt做FFT运算。Tidft是IDFT变换矩阵，可表示为

在式（9）中，Tfft为FFT变换矩阵，可使用高效算法来实现，因而计算的瓶颈在于IDFT变换矩阵Tidft的运算上。下面，基于CZT算法，我们可推导出IDFT变换矩阵的快速实现方法。

将β=fspTsq代入式（8）中，有：

由于

由上述推导可知，IDFT变换矩阵可以使用卷积来实现，具体实现框图见图2。这里需要指出的是，当时域卷积使用频域乘法来实现时，图2中全部的计算量可等价为（2M lb M+3M）次乘法运算，小于式（5）中M2次乘法运算（当M较大时）。

图2 时域离散尺度变换实现框图Fig.2 Temporal applicable structure of the sample rate transformationmethod

由此，我们可推导出合成距离像的离散时域尺度变换处理步骤：

（1）采集N个子带的目标快拍矢量Vpt（p=0～N-1）；

（2）在每个子带内使用前述方法对目标快拍矢量进行处理，即Vpqt=aptTpq-idftTfftSpt=antSqt，其中Sqt是指定的目标时域矢量；

（3）经步骤2处理后，N个子带的目标快拍矢量可表示为［a0tSqt，a1tSqt，a2tSqt，…，aN-1tSqt］，由于各个子带内的目标时域矢量完全相同（相同的Sqt），因而消除了多普勒散布项，则各个子带内后续的多普勒滤波器组都可使用相同的形式来实现（例如FFT），具体实现框图可参见图3。显然，与图1中使用不同参数的DFT处理相比，图3中不但减小了计算量，还可使用FFT来实现每一个子带的多普勒滤波器组，简化了硬件设计；

（4）成像处理（可使用IDFT）。

图3 合成宽带距离像时域离散尺度变换处理框图Fig.3 Temporal changing sample rate processing block diagram of synthetic wideband range profile

3 仿真试验与分析

仿真参数设置如下：第一个子带中心频率为f0=12 GHz，共有128个子带，每一个子带中心频率差和带宽均为Δf=ΔB=5 MHz，脉冲重复频率fr= 5 000 Hz，一个CPI内相干脉冲个数M=20。系统总带宽为B=640 MHz，合成距离分辨单元：ΔR= c／（2NΔf）=0.234 4m。目标由5个散射点组成，各个散射点与第一个散射点的距离间隔为2ΔR、5ΔR、7ΔR、10ΔR，散射点强度之比为1∶5∶3∶2∶7。各个散射点的随机相位是在［0，2π］内均匀分布的随机变量，第1个散射点与雷达的径向距离为450 km +22ΔR。仿真中目标径向速度设为vt=40m／s。

仿真分为两个部分，第一部分是分别仿真出使用尺度变换矩阵和FFT+CZT方法时各个子带的多普勒门输出，第二部分是分别仿真出传统多普勒滤波器组（FFT形式）和基于图3结构的合成距离像。

图4显示了128个子带的目标时域矢量在20个多普勒门的输出情况。由图可知，由于多普勒散布效应，各个子带的多普勒频率不一致，造成多个多普勒门均有输出。

图4 N个子带的多普勒门输出（使用FFT形式）Fig.4 Doppler bin outputs of N subbands（using FFT）

图5 是分别使用了尺度变换矩阵和FFT+CZT方法后，128个子带的目标时域矢量与多普勒门输出的关系。与图4相比，可看出图5中128个子带变换后的目标时域矢量的多普勒频率几乎完全一致。其中，我们特别注意到图5中在分别使用了两种方法后图形保持了很好的一致性，这表明FFT+ CZT方法的性能与尺度变换矩阵是一致的。

图5 N个子带的多普勒门输出（尺度变换矩阵和FFT+CZT方法）Fig.5 Doppler bin outputs of N subbands（usingscale transformationmatrix and FFT+CZTmethod）

图6 为使用传统多普勒滤波器组所合成距离像。由图中可看出，合成距离像出现了严重的形状和位置失真，这与图7形成了鲜明的对比：由于使用了时域离散尺度变换方法（通过FFT+CZT算法快速实现），图中合成距离像与无失真距离像几乎完全一致，有效地消除了由于多普勒散布项所引起的距离像失真。

图6 使用传统多普勒滤波器组所合成距离像Fig.6 Synthetic range profile formed using traditional Doppler filter bank

图7 使用尺度变换方法（FFT+CZT）所合成距离像Fig.7 Synthetic range profile formed using scale transformationmethod（FFT+CZT）

4 结论

本文提出了一种适用于合成宽带雷达信号的离散时域尺度变换方法，其主要特点有：

（1）利用离散时域尺度变换技术，可有效地消除子带间多普勒散布效应，从而获得无失真的合成距离像；

（2）基于FFT和CZT算法，进一步推导出了尺度变换方法的快速实现算法，为该方法的实用化提供了理论基础和具体框架；

（3）当出现多普勒模糊情况时，该方法会由于无法判断正确的多普勒散布项的值而出现距离像严重失真情况，如何解决这个问题是我们后续工作将要研究的重点之一。

［1］Skolnik M I.Introduction to radar system［M］.New York：Mcgraw-Hill Press，1980.

［2］Rabideau D J.Nonlinear synthetic wideband waveforms［C］／／Proceedings of2002 IEEE International Conference on Radar.Edinburgh，UK：IEEE，2002：212-219.

［3］Walbridge M R，Chadwick J.Reduction of range ambiguities by using irregularly spaced frequencies in a synthetic wideband waveform［C］／／Proceedingsof IEEColloquium on High Resolution Radar and Sonar.London，UK：IEEE，1999：9-14.

［4］毛二可，龙腾，韩月秋.频率步进雷达数字信号处理［J］.航空学报，2001，22（6）：16-25. MAO Er-ke，LONG Teng，HAN Yue-qiu.Digital signal processing of stepped frequency Radar［J］.Acta Aeronautica Et Astronautica Sinica，2001，22（6）：16-25.（in Chinese）

［5］王振荣，文宏武.脉间变频格式高距离像分辨力成像方法中系统误差的研究［J］.电子学报，1995，23（12）：82-85. WANG Zhen-rong，WEN Hong-wu.Research on system error of high range resolution imaging by means of pulse to pulse frequency shifting［J］.Acta Electronica Sinica，1995，23（12）：82-85.（in Chinese）

［6］张群，金亚秋.强背景杂波下的地面运动目标干涉式三维成像［J］.电子与信息学报，2007，29（1）：1-5. ZHANGQun，JIN Ya-qiu.Three-dimensional interferometric imaging of a moving ground target in strong background clutters［J］.Journal of Electronics and Information Technology，2007，29（1）：1-5.（in Chinese）

［7］hen Y Y，Liu Y T.A step pulse train design for high resolution range imaging with Dopple resolution processing［J］.Chinese Journal of Electrionics，1999，8（2）：196-199.

［8］彭卫，汪学刚，赵建宏，等.基于常规多普勒滤波器组结构的合成宽带距离像性能分析［J］.航空学报，2009，30（6）：1098-1102. PENGWei，WANG Xue-gang，ZHAO Jian-hong，et al. Analysis of Synthetic Wideband Range Profile Based on Conventional Doppler Filter Banks［J］.Acta Aeronautica Et Astronautica Sinica，2009，30（6）：1098-1102.（in Chinese）

A Synthetic W ideband Radar Imaging System Using Discrete Time Scale Transformation Technology

WEILin
（Aviation Engineering Institute，Civil Aviation Flight University of China，Guanghan 618307，China）

Based on the discrete time scale transformation technology，a new airborne radar imaging system available to the synthetic wideband signal form is proposed.By using scale transformationmatrix，different Doppler frequencies relating to the samemoving target over each subband can be transformed to a known frequency so as to remove Doppler dispersion effect.In thisway，all subbands are able to apply the same traditional Doppler filter bank structure in order to acquire distortionless synthetic range profile（SRP）.At the same time，a corresponding fast computing algorithm is deduced by using FFT and CZT algorithm.The simulation results show the effectiveness and efficiency of the proposedmethod.

airborne radar；synthetic range profile；wideband signal processing；discrete time scale transformation；Doppler filter bank

the M.S.degree from the Northwestern Polytechnical University in 2005. He is now an associate professor.His research direction is avionics.

1001-893X（2011）09-0039-05

2011-05-04；

2011-07-18

TN959.6

A

10.3969／j.issn.1001-893x.2011.09.008

魏麟（1972—），男，四川资阳人，2005于西北工业大学获硕士学位，现为副教授，主要研究方向为航空电子学。

Email：weilin＠cafuc.edu.cn

WEILinwasborn in Ziyang，Sichuan Province，in 1972.He