基于改进PSO-WNN的电能质量扰动分类研究

韩富春 孙碣 令狐进军 郝彩云

(1.太原理工大学 电气与动力工程学院，山西 太原 030024;2.太原供电分公司，山西 太原 030012;3.吕梁供电分公司，山西 吕梁 033000)

0 引言

随着现代工业的不断发展，大量非线性负载和电力电子器件的应用，使得电能质量问题日趋严重。目前对电能质量的检测分析已有多种方法，如小波变换，神经网络，数学形态学等方法，这些方法虽然取得了一定的成果，但还不能完全满足实际工程的需要。本文提出了一种基于PSO-WNN的电能质量扰动分类方法。该方法首先利用小波变换对电能质量扰动信号进行多尺度分解，重构后得到各尺度信号能量的特征向量，然后将特征向量作为PSO-WNN的输入向量进行识别，最后经改进后的粒子群小波神经网络获得电能质量扰动分类结果。由于使用了改进粒子群优化神经网络结构，所以具有收敛速度快，不易陷入局部最优的特点，经实例计算，结果表明该方法具有较强的电能质量扰动分类识别能力。

1 基本原理与方法

1.1 小波多分辨方法

多分辨分析(MRA)是小波分析的一个重要特性，利用MRA对电能质量的检测，是小波分析在电力系统中的重要应用之一［1］。

MRA是由四个元素构成的系统［2］，记为MRAS(Multiresolution Analysis System)，可表示为

其中φ(t)为尺度函数，ψ(t)为 φ(t)对应的小波函数;Vj和Wj(j∈Z)分别是ψ(t)的尺度空间和小波空间。

对φ(t)和ψ(t)进行平移和伸缩可得

设信号函数为f(x)，则在尺度j下的平滑信号为

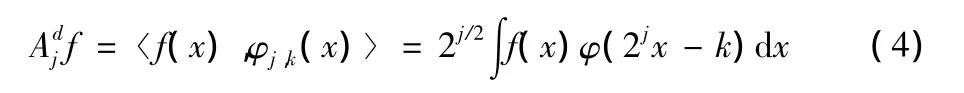
在尺度j下的细节信号为

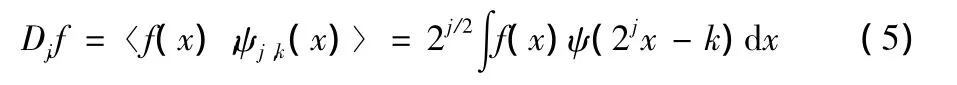
信号f(x)的分解过程是从j+1尺度到j尺度的逐步分解过程，即

其中g和h分别为高通滤波器系数和低通滤波器系数。小波结构树分解如图1所示。

1.2 提取特征向量

首先利用小波变换对电能质量扰动信号进行多尺度分解，分解后得到各小波系数，然后进行重构得到各尺度信号能量组成的特征向量，令其作为神经网络的输入向量。

本文选用db4小波，采样频率为6.4 kHz，对扰动信号进行j个尺度的小波多尺度分解，得到的小波变换系数为dj(k)和aj(k)。由此可得到小波变换能量分布如(7)式

图1 小波结构分解树图

式中 j为分解层数，且 j=1，2，…，J

根据(7)式，采用各特征量构建向量E

将E进行归一化，结果作为小波神经网络的输入向量。

1.3 小波神经网络结构设计

本文选用Morlet母小波［3］，其公式如下

其小波神经网络结构图如图2所示

在本结构中根据小波多分辨分析所确定的特征向量元素，作为小波神经网络的输入节点个数。本文选取输入神经元的个数为7个。

根据小波函数的紧支集取值空间确定节点个数［7］，通过计算本文取隐含层数为13层。

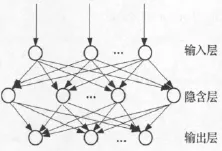
图2 小波神经网络的结构

2 改进PSO算法

粒子群算法是一种简单实用的群集智能计算技术，主要用于求全局最优解。单一的粒子群算法常会出现不收敛和“早熟”现象，本文采用了“粒子进化”和“多粒子群”相结合的改进算法［4］。

改进后的算法公式如下

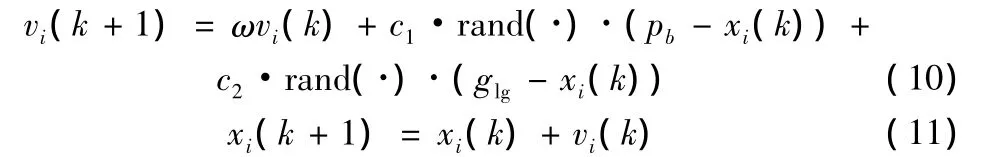
其中ω为惯性因子;c1与c2为学习因子;rand(·)为［0，1］之间随机的数

pb个体最优值;glg为粒子群中各子种群的最优值

本文提出的改进PSO神经网络算法步骤如下

(1)数据预处理，对样本进行归一化运算。

(2)对小波神经网络的参数进行初始化，设定输入层，隐含层，输出层节点个数，将小波的伸缩因子ak，平移因子bk，网络连接权重wik和wk作为粒子的位置向量，即:

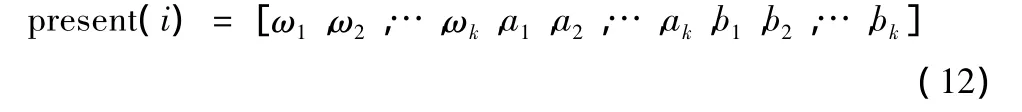
其中k为隐含层节点个数。

(3)计算粒子适应值，更新粒子的当前最优位置pb和全局最优位置glg。

适应值为第d次迭代后网络实际输出y^与期望输出y间的最小均方差

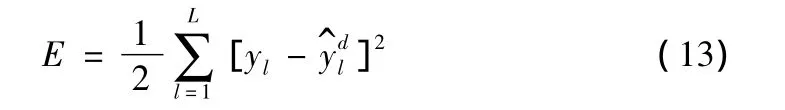
其中d=1，2，…，D，D为最大迭代次数，yl为第l个样本向量输入网络得到的实际输出，y^dl为第l个样本向量经过网络的期望输出。

(4)将新的位置向量输入算法中重新迭代，若迭代次数达到最大迭代次数或者达到预先设定的最小目标差，则停止迭代，否则转到(3)。

(5)搜索全局最优的位置，得到一组接近最优的网络权值，将其代入小波神经网络进一步优化，得到最佳的权值。

(6)根据最佳权值对电能质量扰动进行分类识别。

3 实例分析

本文采集了200个训练样本，其中的100个作为测试样本，100个作为计算样本。分别对小波神经网络算法和改进PSOWNN算法进行识别计算，PSO-WNN计算结果如表1，对比结果如表2所示。

表1 PSO-WNN计算结果表

表2 两种方法计算分类结果表

由表2看出，小波神经网络的整体分类识别准确率为92%，本文方法整体识别率为95%以上，此外本文方法在识别电压暂升和振荡暂态中较WNN识别准确度更高。

4 结束语

本文提出了一种改进PSO-WNN的电能质量扰动分类方法，通过对小波神经网络算法和本文算法的分析比较，结果表明，本文算法使网络的收敛速度更加加快，识别准确率更加提高，从而验证了本文方法的有效性和正确性。

［1］胡铭，陈珩.电能质量及其分析方法综述［J］.电网技术，2000，24(2):36-38.

［2］李建平，唐远炎.小波分析方法的应用［M］.重庆:重庆大学出版社，1999.

［3］McCullough J E，Lands J F.Apollo Comm and Module Land Impact Test［R］.NASA，1970.

［4］刘利芳.粒子群算法的改进及应用［D］.太原:太原理工大学，2009.

［5］郭旭航.小波神经网络在电力谐波检测中的应用［J］.科学技术与工程，2010(11):2784-2788.

［6］侯媛彬，杜京义，汪梅.神经网络［M］.西安:西安电子科技大学出版社，2007:207-210.

［7］徐永海，肖湘宁，杨以涵，等.基于dq变换和ANN的电能质量扰动辨识［J］.电力系统自动化，2001，25(14):24-28.

［8］边海龙，陈光礻禹，杜天军.基于小波神经网络的时变谐波信号检测［J］.中国电机工程学报，2008(7):104-109.

［9］A.M.Gaouda，M.M.A.Salama，M.R.Sultan，A.Y.Chikhani，Power quality detection and classi?cation using wavelet-multiresolution signal decomposition［J］.IEEE Trans.Power Deliv，1999，14(4):1469-1476.

［10］Santo S，Powers E J，Grady W M.Power Quality Disturbance Identification Using Wavelet Transforms and Artificial Neural Networks［J］.In:Proceedings of the 7th IEEE ICHQP，Las Vegas，USA，1996:615-618.

［11］左磊，侯立刚，高大明，彭晓宏，吴武臣.基于粒子群-小波神经网络的模拟电路故障诊断［J］.北京工业大学学报，2010(3):306-309.

［12］Gaing ZL.Implementation of power disturbance classifier using wavelet-based neural networks［J］.In:IEEE Bologna Power Tech Conference;2003.

［13］陈哲，冯天瑾.小波分析与神经网络结合的研究进展［J］.电子与信息学报，2000(3):496-504.