用龙格-库塔法优化一种模糊控制器
2011-06-26王江荣
王江荣
(兰州石化职业技术学院 信控系,甘肃 兰州 730060)
0 引言
带有可自调整因子的模糊控制器输出的一般形式为U=-{α(t)E(t)+(1-α(t))EC(t)}(0<α<1),其中 E(t)和 EC(t)是模糊论域上量化后t时刻的误差和误差变化。α(t)是时刻t的可调整因子(可在线实时调整)。U=U(t)是模糊论域上的输出,其值取决于对误差和误差变化的加权。对可调整因子α(t+1)=α(t)+Δα的在线修改往往根据人们的经验或实验调试确定,这样的修改会有一定的主观性和盲目性。本文利用四阶龙格一库塔公式逼近被控对象,再结合梯度下降法实现了可调整因子中的Δα(t)中的在线修改和在线优化,仿真曲线表明,在响应时间相同的情况下,具有优化后的调整因子的模糊控制器在稳定时间、超调及鲁棒性等几方面的性能均优于未优化的模糊控制器,显著地改善模糊控制系统的控制精度和稳态性能。
1 龙格-库塔
龙格-库塔法是求解常微分方程初值问题的有效数值方法。这种方法的特点是区间[xk,xk+1]上取N个点,以这N个点的斜率值f(xk,yk)的线性组合为加权平均斜率,构造近似公式
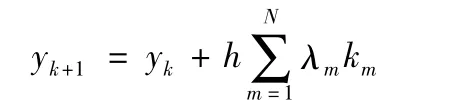
其中 k1=f(xk,yk)
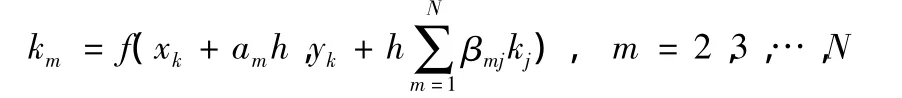
确定这些常数的原则和方法是:将精确解y(xk+1)在xk作Taylor展开,ki在(xk,y(xk))点作二元Taylor展开,将展开式按h的幂次整理后,令h0,h1,h2,…等项的系数为零,使Tk+1首项中 h的幂次尽量高。
在近似公式中取N=4,可得到四阶龙格-库塔法公式yk+1其中 k1=f(xk,yk)

四阶龙格-库塔法的优点是它的精确度高且是一步法,即已知yk就可以算出yk+1,另外容易用程序实现。
2 可调整因子α(t)的自动优化过程
设t时刻的可调因子值为α(t),t时刻算出的α(t)的增量为Δα(t),t时刻后算出的修改因子为 α(t+1)=α(t)+Δα,Δα 可由t时刻采样所得的误差e(t)求得。对α(t)的实时修改和优化具体推理过程如下:
设t时刻的误差e(t)和误差变化ec(t)量化后得到模糊论域上的误差为E(t)和误差变化EC(t),则t时刻模糊控制器在模糊论域上的输出为

该输出乘以输出比例因子Ku就得到t时刻的控制器的实际输出 u(t),即
设被控对象的状态方程(可用MATLAB软件将被控对象的传递函数H(s)转化为状态方程)
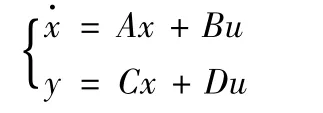
其中,A,B,C,D 是系数矩阵。u为式(1)。
用龙格-库塔法逼近被控对象如下

则t+1时刻系统的输出为

t+1时刻的误差
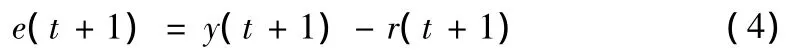
这里的r(t+1)是系统输入。
Δα(t)的计算
这里的λ和μ是比例系数。
按负梯度方向求t时刻可调整因子α(t)的增量Δα(t),即
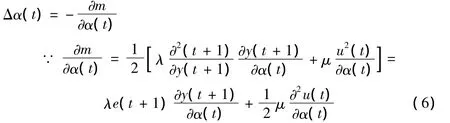


由(2)可得
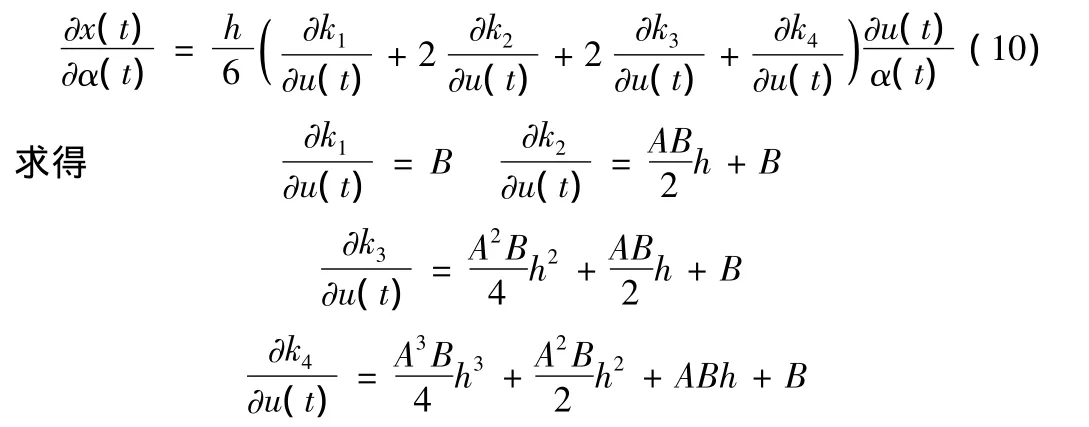
将上四式代入(9)得

将(8)、(9)及(11)代入(7)得
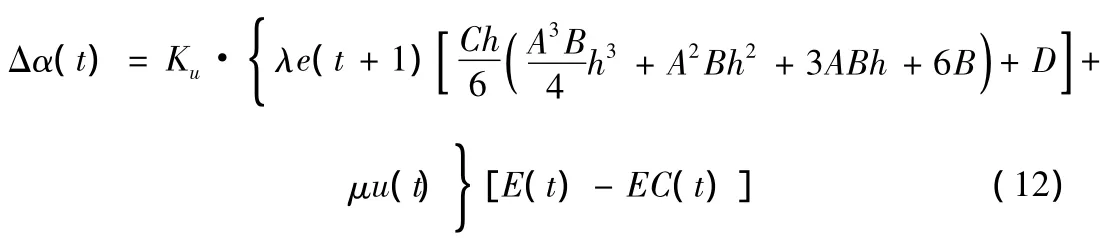
当系统确定时,即A,B,C,D及h确定时

由(12)知只需调整参数β和γ就能计算出Δα(t)(并不依赖状态方程中的系数矩阵),进而实现对模糊控制器的优化。
3 仿真结果
利用MATLAB进行仿真实验
(2)假设系统的模型可以用二阶加纯滞后表示,即传递函数为采样时间间隔为 ΔT=0.01 s,输入为阶跃函数r(t+1)=1.5,α 的初始值取 0.5,β=0.065,γ =0.015时,系统的输出响应为如图2中的曲线1.图2中的曲线2是没有加修改的 Δα(t)的情形。可以看到用龙格-库塔法进行修改 Δα(t),模糊控制器的输出曲线上升时间短(到达稳态),且具有很好的稳态性能(振荡幅度小),说明本文方法起到了优化效果。

4 结束语
本文利用龙格-库塔法改进了自寻优模糊控制器的可调因子α(t),实现了对α(t)的在线实时优化。从仿真曲线表明,在响应时间相同的情况下,具有优化后的调整因子的模糊控制器在稳定时间、超调及鲁棒性等几方面的性能均优于未优化的模糊控制器。它最大限度地识别和利用控制系统所提供的信息,不断的修正控制规则,使控制器本身的控制规律适应系统的需要,从而显著地改善模糊控制系统的控制精度和稳态性能。
[1]李国勇.模糊控制神经控制和智能控制论及应用[M].北京:电子工业出版社,2010(1):164-224.
[2]雷德明.一种新型自学习模糊控制器[J].信息与控制,2000,29(6):559-562.
[3]李荣华,等.微分方程数值解法[M].北京:高等教育出版社,2002(8):59-60.
[4]侯忠生.非参数模型及其自适应控制理论[M].北京:科学出版社,1999:30-80.
[5]刘航,徐社.MATLAB在模糊控制系统设计与仿真中的应用[J].计算机应用研究,2001(1):27-28.
