基于Hopf分岔理论的风电系统电压稳定性研究

李季 周雪松 马幼捷

(天津理工大学 自动化学院，天津 300384)

0 引言

近年来，风力发电在世界范围内发展迅猛，风电并网乃是风电发展的必然选择。然而随着风电容量在电网中的比例迅速增加，风电对电网的影响日益突出［1-2］。大规模的风电接入可能会影响电能质量、线路传输功率越限、短路容量增加及电力系统稳定性发生变化等问题。国内外风电场运行经验表明，大规模风电入网产生的联网问题主要是电压稳定问题，电压失稳是含风电的电力系统(下文简称风电系统)失稳的主要形式［2］，这给大规模风电利用带来了巨大的挑战。

正是由于分岔理论在常规电力系统电压稳［1］定性研究中的丰硕成果［3-5］，结合风电系统的非线性动态特征，分岔理论被引入来研究风电系统电压稳定性［6-7］。而目前风电系统分岔研究大都是基于鞍结分岔研究［8-9］，很少涉及风电系统的Hopf分岔的研究。Hopf分岔是电力系统极限运行点的标志之一，对常规电力系统研究表明:发生Hopf分岔的系统都运行在接近“鼻形曲线鼻尖”部分，此处运行点的吸引区域非常小，系统抗扰性差。因此应用Hopf分岔理论研究风电系统的电压稳定性也就很有意义。

本文应用Hopf分岔理论，研究了异步发电机等值的风电场的有功功率和无功功率对风电系统电压稳定性的影响;并对静止无功补偿器(static var compensation，SVC)对Hopf分岔的控制作用进行了分析，以期得到一些对风电系统稳定运行有参考价值的结论。

1 HOPF 分岔理论简介［10］

非线性动力系统的参数变化不能使系统从一种流连续地过渡为另一种流的现象称为分岔，分岔理论主要包括静态和动态两个方面。静态分岔指的是平衡点的数目和稳定性随参数变化而发生的变化，如鞍结分岔。动态分岔则是对系统结构稳定性的否定，对于结构不稳定的系统，一个小扰动就可能破坏轨线的拓扑等价，Hopf分岔是最基本也最具有代表性的动态分岔。

对于非线性动力系统，其运动方程一般为

式中μ∈R是分岔参数，如果在平衡点(x0，μ0)处的系统的Jacobian矩阵有一对纯虚非零特征值，这对虚根横截的穿越虚轴时，在临界点附近会出现周期解，即为Hopf分岔，Hopf分岔也可以理解为形成极限环或周期解的分岔。

Hopf分岔理论研究的是自治系统平衡点解分岔产生稳态周期解的问题，基本思想是基于经典稳定性理论，从方程的摄动方程零解稳定性来判别平衡点解的稳定性。Hopf证明了系统在(x0，μ0)处将从平衡点解分岔出一个非常量的周期解，即对应系统的极限环，系统发生振荡或振荡失稳，在电力系统中就发现了这种现象。因此追踪系统平衡解流形、确定分岔点位置，对于了解电力系统稳定性及其变化规律有重要的意义。

2 平衡解流形的追踪［11］

对于动力学系统

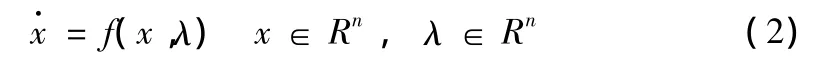
式中x为状态变量，λ为控制参数。

若系统式(2)在平衡点(x，λ)处满足霍普夫分岔，则在该系统的雅可比矩阵A≡∂f/∂x在该点处分别对应一对共轭纯虚根，记为jω。对霍普夫分岔，有

上述方程为复数形式，即向量q和q0。该方程的未知数为(x，λ，q，ω)，可以分析方程个数和未知数的个数是相等的。

式(2)的平衡点满足方程f(x，λ)=0，可以认为，该方程在n+1维空间y≡(x，λ)∈Rn×R1定义了一个1维的广义曲线(或称流形)M，称之为平衡解流形或平衡解曲线，而延拓法可用来追踪该流形，它是用一系列满足平衡点要求的离散点(y1，y2，…)来逼近曲线M的。在追踪该流形的过程中，通过检测局部分岔条件来判断是否在该流形上存在分岔点。一般延拓法只能追踪计算得到一维流形，因而也只能计算得到单个参数的分岔值。

为了追踪风电系统二维参数分岔边界。现假设已算得式(2)的单个参数分岔点，由此可探索将延拓法应用于求解直接法所处理的数学方程。其意义等价于利用延拓法来追踪局部分岔所满足的流形，而非上述意义下平衡解流形，此时可计算得到式(2)中二维参数的局部分岔边界。本文利用这种思想来求取风电系统的二维分岔边界。

3 风电系统Hopf分岔算例分析

3.1 风电系统模型

本文采用的风电系统模型，如图1所示。该模型由一个等值风电场和两个发电机组成，其中发电机G1母线被处理成松弛母线，等值发电机G2采用二阶模型，风电场G3采用动态Walve负荷模拟。

3.1.1等值发电机模型

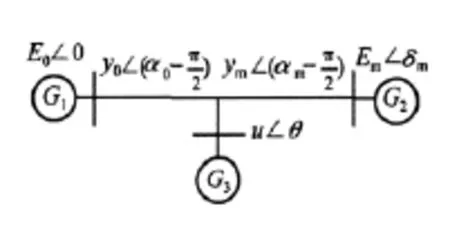
图1 风电系统模型

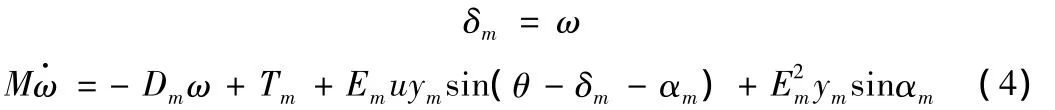
其中M、Dm、Tm和Em分别为发电机的惯量、阻尼系数、输入转矩和发电机机端电压;δm、ω、θ、u分别为发电机功角、发电机角频率、节点电压相角、节点电压;ym和 am为网络参数。

3.1.2风电场模型

异步发电机是目前风力发电中应用较广泛的机型，由于异步发电机运行时输出的有功功率的大小取决于风速和风向，和系统负荷变化无关;同时异步发电机组运行时要从电网吸收无功功率，势必会引起电网电压的降低，尤其会引起风电场与电网联络线的电压损耗增加。

为了研究风电场的异步发电机组发出的有功功率和吸收的无功功率对风电系统电压稳定性的影响，所以可以把风电场等值为电力系统的特殊动态“负荷”，动态负荷模型［12］如下

其中P为风电场发出的有功功率;Q为风电场吸收的无功功率，P1+jQ1为感应电动机并联的静态恒功率负荷，对于风电场P1就对应风速转化的有功功率，其余参数含义见文献［13］。

3.1.3风电系统模型

将系统各元件模型和网络方程联立就可以得到描述系统的综合模型，一般形式为，其中 f定义了发电机和负荷的动态行为。系统的状态变量x=［δm、ω、θ、u］，变量的含义，式中参数的含义及推导可参阅文献［13］。

3.2 仿真分析

电力系统Hopf分岔是一种很重要的动态分岔，是其余动态分岔的基础。电力系统中的Hopf分岔与参数有密切的关系，不同的参数对Hopf分岔的影响不同。本文针对有功功率和无功功率对Hopf分岔的影响进行研究。

3.2.1有功功率和无功功率对Hopf分岔的影响

在电压稳定分析中，当系统的无功功率Q1发生变化，使系统电压处于稳定或不稳定平衡点状态时，对应的系统电压稳定或不稳定;图2给出了风电场端电压u随无功功率Q1变化而发生分岔的情况，系统平衡解流形的下半个分支是不满足运行要求的的，所以把分析的重点就放在平衡解流形的上半支上。

从图2可以看出，从初始状态Q1=0，u=1 开始，随着风电场吸收的无功功率Q1的增加，风电场电压u持续下降，在系统达到运行极限点 LP(limit point)之前，即风电系统 Q1达到1.499884时，系统发生Hopf分岔，即图2中的H1，此时系统电压(u=0.908584)满足运行要求时，由Hopf分岔理论可知，当系统发生Hopf分岔时，对应的系统开始出现振荡，所以风电场消耗的无功功率会对系统的动态电压稳定性产生影响。

风电场运行时，有功功率和无功功率都在变化，所以对风电场进行两参数的Hopf分岔研究更有意义，图3给出了当P1和Q1同时变化时系统的二维电压Hopf分岔边界，随着有功功率P1的增加，系统的电压u升高，随着无功功率Q1的增加，系统电压u降低，相应的，随着风电场无功功率的增加，造成了风电场在发出较少的有功功率时，就可能发生Hopf分岔，即为了避免系统发生Hopf分岔，当无功功率消耗较大时，必须限制风电场的有功功率的输出，所以Hopf分岔的消失是以牺牲风电场的有功出力为代价的。

3.2.2静止无功补偿器SVC对Hopf分岔的影响

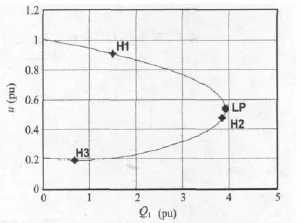
图2 Q1对风电系统Hopf分岔的影响

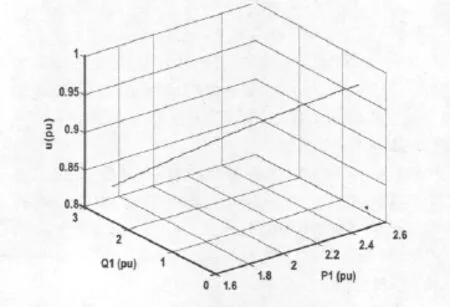
图3 P1和Q1对风电系统Hopf分岔边界的影响

Hopf分岔的出现有可能导致电力系统的电压崩溃，因此控制系统中的分岔是避免电压崩溃的一种途径。通过前面分析P1、Q1，y0对风电系统电压稳定性影响分析，可知系统发生Hopf分岔和风电场吸收的无功功率有密切关系，而静止无功补偿器SVC作为动态无功补偿装置，是实现分岔控制的有利工具。

图4 加装SVC的风电系统模型

本文采用在上述风电系统的风电场端安装SVC，如图 4所示，数学模型如式 5所示。

式中，uref为参考电压，u为补偿点电压，Kr和 Tf为控制器放大倍数和时间常数，bSVC为等值电纳，发出无功功率Q=bSVCu2。

本文以Q1对风电系统 Hopf分岔点的影响为例，说明风电场在加装SVC之后，Q1的变化对系统分岔点和电压稳定性的影响。图5给出了Kr=1.5和Tf=0.02时的风电系统分岔参数Q1对加装SVC后的风电系统Hopf分岔点的影响，通过与图2比较可知，加装SVC后的风电系统，当 Q1增加时，系统的电压提高了，同时系统发生Hopf分岔时的的无功功率(Q1=11.531989)大大提高了，且Hopf分岔点H1点非常接近于系统的极限运行点LP，如图6所示，仿真表明SVC为风电场提供的无功功率，延迟了Hopf分岔的发生，增加了风电系统的稳定域。

4 结束语

风电系统随着无功功率消耗的增加，会降低风电场的电压水平，同时相应要限制风电场的有功出力，以避免Hopf分岔对风电系统电压稳定性的影响。SVC作为动态无功补偿设备，可以延迟系统的Hopf分岔点，增加负荷极限，提高了风电系统系统的电压稳定性。

［1］Driesen J，Belmans R.Distributed generation:challenges and possible solutions［C］.2006 IEEE Power Engineering Society General Meeting，Montreal，Canada，2006.

［2］孙涛，王伟胜，戴慧珠，等.风力发电引起的电压波动和闪变［J］.电网技术，2003，27(12):62-67.

［3］李宏仲，程浩忠，朱振华，等.分岔理论在电力系统电压稳定研究中的应用述评［J］.继电器，2006，(04):69-73，79.

［4］李宏仲，程浩忠，滕乐天，等.以简化直接法求解电力系统动态电压稳定分岔点［J］.中国电机工程学报，2006，26(8):28-32.

［5］江伟，王成山，余贻鑫，等.直接计算静态电压稳定临界点的新方法［J］.中国电机工程学报，2006，26(10):1-6.

［6］ZengG Zhiyuan，Li Xianqi，Zhou Jianzhong，et al.Investigation of Wind Farm on Power System Voltage Stability Based on Bifurcation Theory［C］.Power and Energy Engineering Conference，APPEEC 2009.Asia-Pacific:1-4.

［7］Ami Radunskaya，Robert Williamson，and Robert Yinger.A Dynamic Analysis of the Stability of a Network of Induction Generators［J］.IEEE TRANSACTIONS ON POWER SYSTEMS，2008，23(2):657-663.

［8］马幼捷，张继东，周雪松，等.基于分岔理论的含风电场电力系统静态电压稳定问题研究［J］.电网技术，2008，32(9):74-79.

［9］马幼捷，问虎龙，周雪松，等.基于延拓法的风电系统稳定模型二维参数分岔边界的计算与研究［J］.中国电机工程学报，2011，30(19):26-30.

［10］罗成，程时杰，江全元.电力系统次同步谐振中 Hopf分岔现象的研究［J］.继电器，2002(05):1-5.

［11］曹国云，刘丽霞，赵亮，等.基于延拓法的电力系统稳定模型中二维参数局部分岔边界的计算［J］.中国电机工程学报，2005，25(8):13-16.

［12］刘邵峰，高金峰，李鹏.基于 Walve负荷模型典型电力系统多参数分岔分析［J］.继电器，2004(19):13-17，33.

［13］Dobson L，Chiang Hsino-dong，James S，et al.A Model of Voltage Collapse in Electric Power Systems［A］.In:IEEE Proceedings of 27th Conference on Control and Decision［C］.1988:2104-2109.