基于不完全扑灭的应急物资最优分配决策模型
2011-06-26庞海云
庞海云
应急物流是为应对严重自然灾害、突发性公共卫生事件、公共安全事件及军事冲突等突发事件,从而对物资、人员、资金的需求进行紧急保障的一种特殊物流活动。它具有突发性、不确定性、非常规性及弱经济性等特点[1]。城市是人口高度集聚地区,一旦发生突发性公共事件,各个受灾点急需大量的应急物资,如食品、救援设备、药品等,这时需要通过应急物资分配来完成[2-3],以降低突发性公共事件带来的后继损失,加快重建工作。若应急物资分配不当,则会影响城市机能恢复,势必造成更加巨大的损失。应急物资分配非常重要,决定了救灾减灾的效果。
人们针对不同的目标、背景和要求对应急物资分配开展了研究。在建模方面,汪欲等[4]以出救点数目最少、出救时间最短为目标,Ray[5]、Rathi[6]、Equi[7]在不同的约束条件下以最小化运输费用为目标,Özdamar[2]以所有应急物资的未满足需求之和最小为目标,将多商品应急物资分配问题与车辆调度问题结合起来建立模型。关于求解模型的算法研究,目前为止,应用和发展了许多优化技术和方法。如Sheu[8]针对建立的救灾阶段应急物资的联合分配模型,提出了一种混合模糊聚类优化方法来求解;Yi等人[9]用蚁群算法求解车辆路径选择和多商品调度问题的模型;Özdamar[2]和缪成等[10]应用拉格朗日松弛法求解模型。
分析现有国内外相关文献后,笔者认为可以在以下方面进行改进:首先,决策以系统损失最小为目标,更能反映应急物资分配的基本原则,因为灾后最重要的事情是以最有效的方式来减少生命和财产损失[11],与节省时间和成本相比较,减少损失应该是第一位的;其次,在由于供给短缺或运力限制造成灾害无法全部扑灭(即不完全扑灭)的情形下,应考虑如何通过全局优化保证不同受灾点物资分配的相对公平性;研究对象扩展到对多个出救点、多个受灾点、多种物资的分配,这是应急物资分配中更真实的情况。
本文将沿着以上思路构建城市应急物流中不完全扑灭的物资分配决策模型,即将完全扑灭供给的研究扩展到不完全扑灭供给情形,将单出救点或单种物资分配模型扩展到多出救点、多种物资分配的模型,并从理论上分析最优性条件,利用优化技术求解模型的最优解。
1 问题的描述及数学模型
1.1 问题的描述
设有l个出救点,存储m种应急物资,n个受灾点,第i(i=1,…,l)个出救点储存应急物资j(j=1,…,m)的存储量为aij,受灾点k(k=1,…,n)对物资j的需求量为djk,dj为全部受灾点对物资j的总需求量,为出救点i到受灾点k的运力,现假设不同应急物资能够混载,各受灾点对各种物资的最低保障率为e。要求给出一方案,确定出救点i分配到受灾点k的第j种物资的数量Sijk,同时保证物资分配方案能够尽量减少各受灾点的系统损失,并兼顾受灾点的相对公平。
1.2 数学模型
针对上述问题的背景、目标和要求,建立数学模型如下。
1.2.1 决策变量
1.2.2 目标函数

1.2.3 约束条件

其中,式(2)表示从出救点i发出的应急物资j的总量不大于其储备量;式(3)表示各个受灾点的运力限制,从各出救点分配到各个受灾点的物资总量不能超过该受灾点的运输能力;式(4)表示各个受灾点的需要量限制,从各出救点分配给每个受灾点的每种物资的总量不能超过该受灾点对该种物资的实际需求量;式(5)为物资分配的相对公平约束;式(6)为非负约束。
2 模型求解分析
2.1 利用MATLAB优化工具箱求解
本模型为目标函数为非线性的约束优化问题。求解此问题本研究选择MATLAB语言实现,是因为MATLAB相对于其他包括FORTRAN和C在内的多种高级语言来说,不仅具有语言简洁紧凑、库函数丰富等优点,而且具有功能强大的工具箱,特别是优化工具箱对于求解非线性规划非常方便。优化工具箱中fmincon函数使用较多,用此函数迭求解约束优化问题迭代次数少,但是如果有多个不同局部最优解,不同的初值会收敛到不同的值,所以使用该函数求解必须证明模型是凸规划问题,如果这个结论成立,则可以说明问题的任何局部最优解也是其全局最优解。
根据凸规划的定义首先证明目标函数L是凸函数,则需证明其Hessian矩阵是半正定阵,经计算Hessian矩阵是由l×l个相同的对角阵组成的一个实对称阵,而对角阵的对角元素是目标函数L对决策变量的二阶偏导数,即:

由于α≥1,因此二阶偏导数非负,经计算Hessian矩阵的左上角各阶主子式都大于等于零,则Hessian矩阵是半正定阵,故目标函数L为凸函数。又因为所有约束条件都是线性函数,则把约束式(2)、(3)、(4)看成是凸函数,把约束式(5)、(6)看成是凹函数,则可以证明该模型为凸规划,所以模型可以用fimincon函数求解。
使用fmincon函数时选用中型算法(序列二次规划法),在每步迭代中求解二次规划问题,并用BFGS法更新拉格朗日Hessian矩阵。具体求解过程分为3步:第一步,建立M 文件定义目标函数;第二步,建立M 文件定义约束条件;第3步,激活优化工具箱,选择选项“fmincon”和“Active set”,把2个 M 文件名及初值输入,点击“start”即可获得最优方案。
2.2 模型应用举例
设某洪涝灾区有4个受灾点,由于受灾点的建筑结构、人口分布、天气情况都有差异,所以受灾程度不同,对各种物资的需要量也不同。各受灾点对药品、设备、食品、衣物和帐篷5种应急物资的需求情况如表1所示。
设有2个出救点,表2表示各个出救点储存的几种应急物资的数量aij,表3表示各出救点到各受灾点的运力cik。
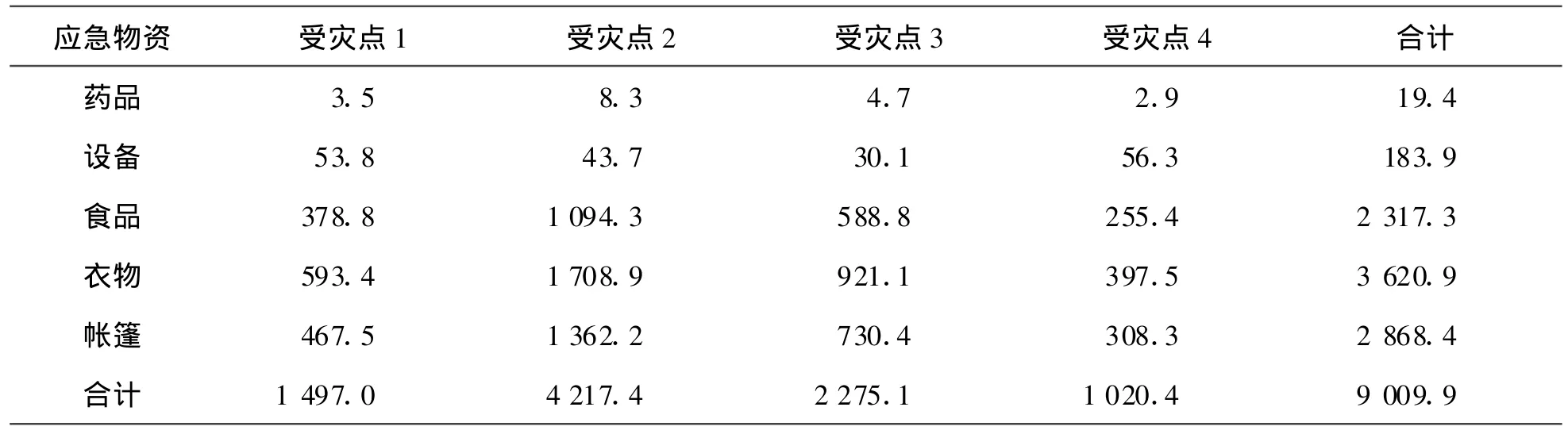
表1 各受灾点的应急物资需求情况Table1 Demand for each type of relief commodity in each affected area t

表2 出救点可供应的应急物资情况Table 2 Storage of each relief commodity in depot t

表3 出救点到各受灾点的运力情况Table 3 Transport capacity from depot to each affected area t
根据物资的作用和其对受灾人员的重要性,设定物资系数ω′j。根据各个受灾点的属性(如在地震中受灾点房屋损坏程度、次生灾害发生情况、天气情况等)和受灾人员的属性(如受灾人员的受伤程度、年龄、性别、饥饿时间等)设定受灾点系数 ω′jk。根据公式 ωjk=ω′j×ω′jk,求出差异系数 ωjk如表4所示。
根据各种应急物资的储备情况和出救点到各受灾点的运力情况设定公平度系数e。各种物资储备量与其需求量的最小比值为0.790,出救点到各受灾点的运力与各受灾点物资需求量的最小比值为0.782,则公平度系数e必须小于这两个比值的最小值,即小于0.782。则设公平度系数e为0.70。
当灾害指数α=2时,使用MATLAB7.9的fmincon函数,得到最优目标函数值为0.125 5,最优解及各受灾点各种物资的满足率如表5所示。

表 4 差异系数 ωjkTable 4 Difference indexωjk

表5 α=2时的最优解Table 5 Optimal solution whenα=2
从总体来看,各受灾点获得药品的满足度是最高的,其次是救援设备,说明在运力有限的情况下,比较重要的物资优先得到分配;而对于同一应急物资,受灾点对其需求的紧迫性越大,其满足率也相对较高,如受灾点3相对其他受灾点对设备的需求比较紧迫,所以满足率也是最高的(84%),说明物资优先分配到对物资需求比较紧迫的受灾点。
如果去掉式(5)的公平约束,重新求解,得到最优目标函数值为0.082 5,最优解及各受灾点物资的满足率如表6所示。

表6 α=2时的最优解无公平约束Table6 Optimal solution whenα=2(without equity constraints)
观察表6的数据可以发现,在无公平约束情况下,各受灾点的物资满足率分布很不均匀,最高的药品的分配几乎达到100%,而最低的衣物满足率只有24.8%,远远低于设定的公平度系数0.7,未达到这个指标的共有6个,其中有6个是对受灾点4的分配,如此分配方案对其来说是非常不公平的。由此验证了没有公平约束,很难保证最优分配方案的公平性。
对比具有公平约束和不具有公平约束情况下的目标函数值可以发现,具有公平约束条件下的系统损失更大,也就是说相对公平的物资分配方案的实现是以增加系统损失为代价的。如果系统增加的损失在可以接受的范围内,那么公平约束还是有很大意义的。
如果把灾情指数α取不同的值,损失函数的最优取值如表7所示。可以看到当α比较小时,损失函数相对比较大,而随着α值的增大,损失函数减少,而且有无公平约束对函数值的影响也同时减少,这就是说,当灾情比较严重时,应用此模型可以在系统效率提高的同时兼顾公平,即达到效率与公平的统一。

表7 不同α值时的损失函数比较Table7 Comparison of loss functions with differentα
3 结 语
在分析城市应急物资分配研究现状的基础上,本研究在构建多出救点、受灾点、多种应急物资分配决策模型时,以受灾点系统损失最小为目标,考虑了公平约束。本研究构造的系统损失函数考虑了各种应急物资的重要性和各受灾点对物资的需求紧迫性,以及受灾程度。在理论上证明了该模型是凸规划后,提出用MATLAB优化工具箱的fmincon函数求解具有速度快且没有初解依赖性,能够得到全局最优解,最后用一个算例证明模型的有效性。但是本研究所构建的模型为静态的,而实际情况具有动态性,如需求量、供应量、运力条件及差异系数是随着时间变化的,因此需研究各种参数的动态演化规律,这些有待作进一步的研究。
[1] 高东椰,刘新华.浅论应急物流[J].中国物流与采购,2003(23):22-23.
[2] ÖZDAMAR L,EKINCI E,KUCUKYAZICI B.Emergency logistics planning in natural disasters[J].Annals of Operations Research,2004,129(1):217-245.
[3] YI W,ÖZDAMAR L.A dynamic logistics coordination model for evacuation and support in disaster responseactivities[J].European Journal of Operational Research,2007,179(3):1177-1193.
[4] 汪欲,何建敏.应急系统中多资源出救方案的研究[J].东南大学学报:自然科学版,2002,32(3):510-513.
[5] RAY J.A multi-period linear programming model for optimally scheduling the distribution of food-aid in West Africa[D].University of Tennessee,Knoxville,TN,1987.
[6] RATHI A K,CHURCH R L,SOLANKI R S.Allocating resources to support a multicommodity flow with time window[J].Logistics and Transportation Review,1992,28:167-188.
[7] EQUI L,GALLO G,MARZIALES,et al.A combined transportation and scheduling problem[J].European Journal of Operational Research,1997,97(1):94-104.
[8] SHEU J B.An emergency logistics distribution approach for quick response to urgent relief demand in disasters[J].Transportation Research Part E,2007,43(6):687-709.
[9] YI W,KUM ARA.Ant colony optimization for disaster relief operations[J].Transportation Research Part E,2007,43(6):660-672.
[10] 缪成,许维胜,吴启迪.大规模应急救援物资运输模型的构建与求解[J].系统工程,2006(11):6-12.
[11] HAGHANI A,OH S C.Formulation and solution of a multi-commodity,multi-modal network flow model for disaster relief operations[J].Transportation Research Part A,1996,30(3):231-250.
