基于稳态模型异步电机的效率优化控制策略

黄日俊

（柳州五菱汽车工业有限公司，广西 柳州 545007）

在电动汽车的电机驱动方案中，矢量控制的感应异步电机目前被普遍采用。感应异步电机结构简单，制造工艺成熟，有过载能力强、弱磁控制容易等优点，其缺点是在轻载运行时的效率会降低。而电机的运行效率，直接决定电动汽车运行的经济性，因此如何提高异步电机在低载工况下的运行效率，受到关注，并且有较高的应用价值。

1 效率最优控制思想

异步电机的损耗由铁耗、铜耗、机械损耗和杂散损耗构成，其中铁耗、铜耗为主要损耗。通常情况下，铁耗、铜耗占总损耗的80%～90%，因此异步电机效率最优控制，是运用相应的控制策略，使得电机铁耗与铜耗的总和最小。

由电机理论可知，电机铁耗与磁链成正比，电机铜耗与电流的平方成正比。在矢量控制的算法中，将电机定子电流解耦为正交的激磁电流分量isd和力矩电流分量isq。

其中，isd与电机磁链近似成正比，也近似正比于电机铁耗，力矩电流分量isq2正比于铜耗。通过对isd和isq的单独控制，改变电机的运行转速、转矩和功率。

以电机转矩为例，电机转矩与isd和isq围成的矩形面积成正比，对于电机运行的任一扭矩值，可以有无数的isd和isq的组合与其对应，而其中isd的降低，必然会导致isq的上升，反之依然。

由此可得异步电机效率最优控制思想是：由电机的转速和转矩给定指令，调整定子电流中的激磁电流分量isd和力矩电流分量isq的大小，目标是使得电机的铜耗与铁耗之和最小，通常的做法，是在异步电机的轻载工况采取弱磁策略，即减小isd。

2 效率最优控制的理论推导

异步电机是一个多变量、高阶、强耦合的非线性系统，为了便于分析研究，对实际电机进行如下假设，抽象出理想化电机模型：

（1）三相定子绕组和转子绕组在空间均对称分布，即在空间互差120°电角度，所产生的磁动势沿气隙圆周按正弦分布，即忽略空间谐波；

（2）忽略磁路饱和的影响；

（3）忽略定、转子的漏感；

（4）不考虑频率和温度变化对电阻的影响。

在上述假定条件下，异步电机在任一两相坐标系中的动态数学模型抽象如下：

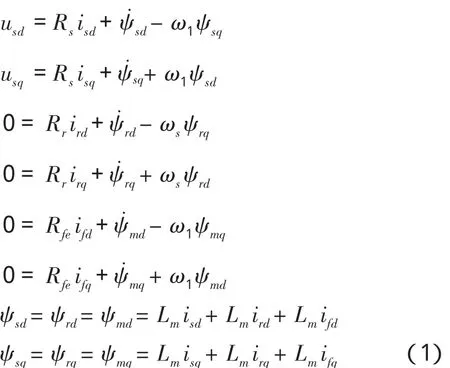
式中，

Rs、Rr、Rfe为定、转子绕阻电阻及铁损等效电阻；

Lm为定、转子绕阻间的互感；

ifd、ifq为两相坐标系中d、q轴铁损等效绕阻电流；

isd、isq、ird、irq为 d、q 轴的定、转子电流；

ψmd、ψmq为 d、q 轴主磁链；

ψsd、ψsq、ψrd、ψrq为 d、q 轴定、转子磁链；

usd、usq为 d、q 轴定子电压。

电机动态等效模型如图1所示。

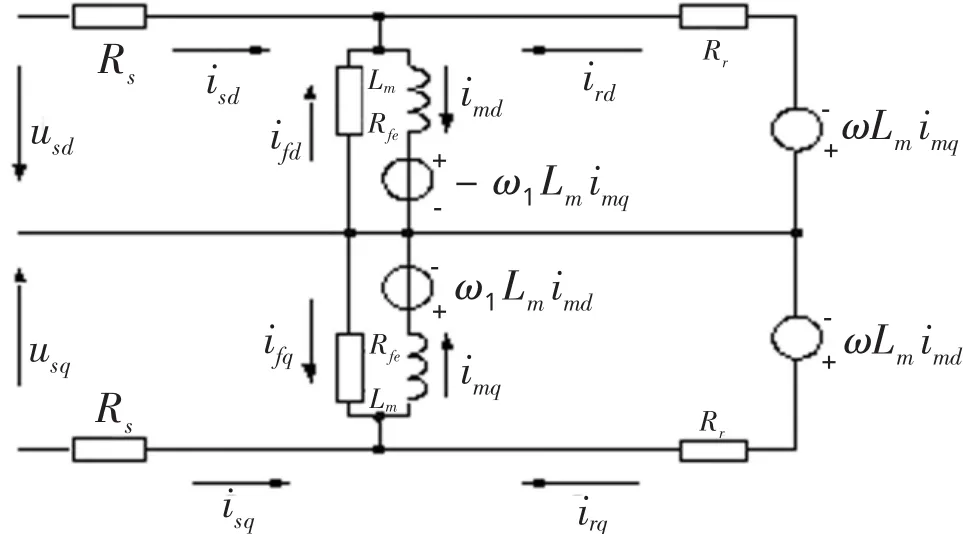
图1 考虑铁耗并忽略定转子漏感时d、q坐标系下电机动态等效模型

为了简化分析过程，将d、q坐标系按转子磁场定向。在转子磁场坐标系下有

ψrd=ψr；

ψrq=ψsq=ψmq=0，

将模型进一步简化，当电机稳定运行时，电流的d、q轴分量为直流，其导数为0，推出电机的稳态方程为

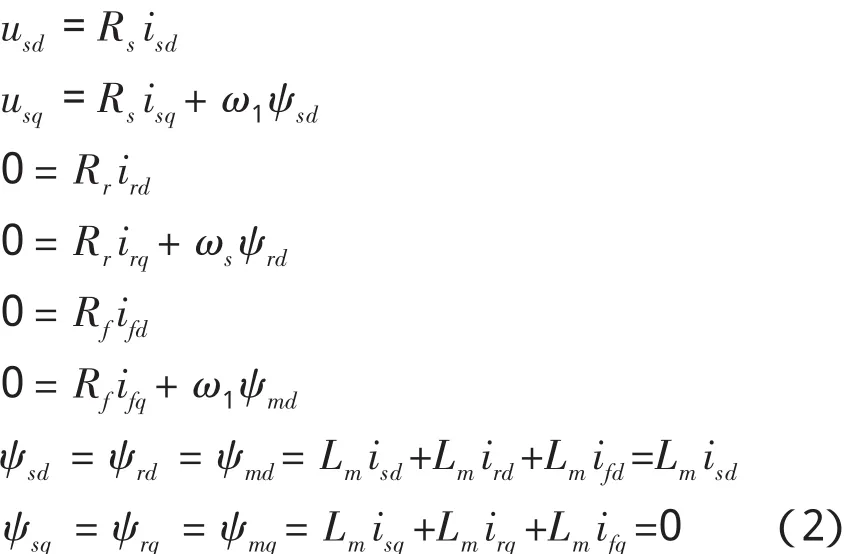
由上式可得出

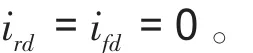
由此作出电机的稳态等效模型如图2所示。

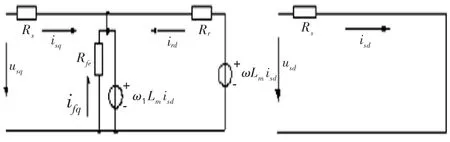
图2 转子磁场定向异步电机的稳态等效模型

由该模型，列方程如下：

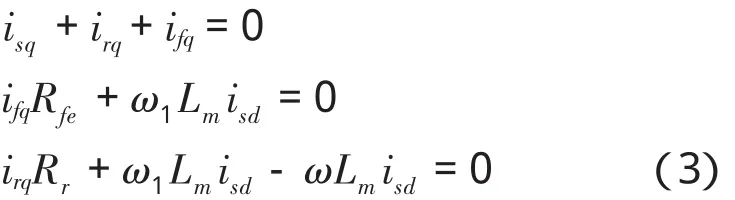
令isqm=isq+ifq，irqm=irq

解此方程组得

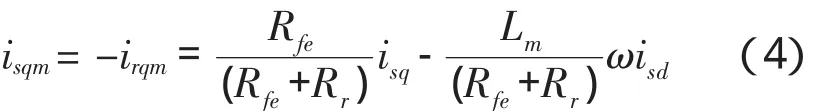
定子铁损为

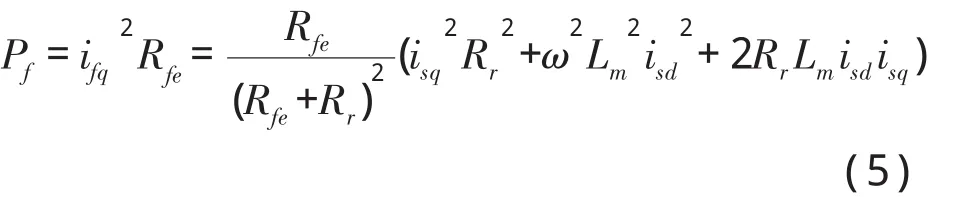
由此，定子铜耗为

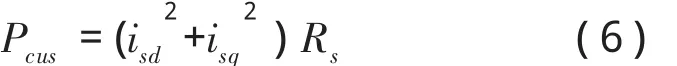
转子铜耗为

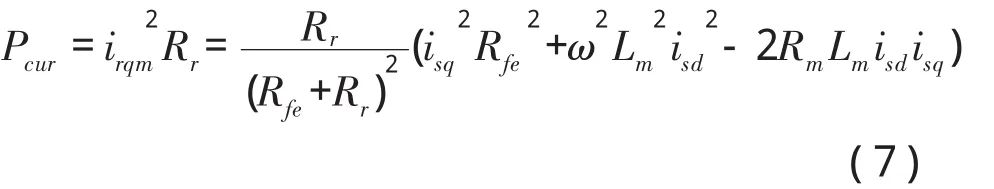
电机总损耗为

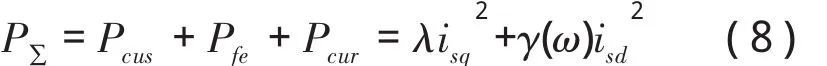
式中，

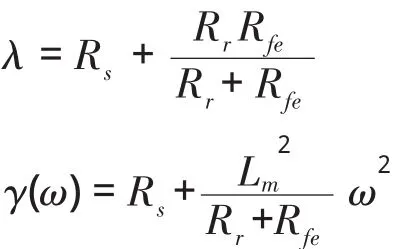
感应电机的电磁转矩为

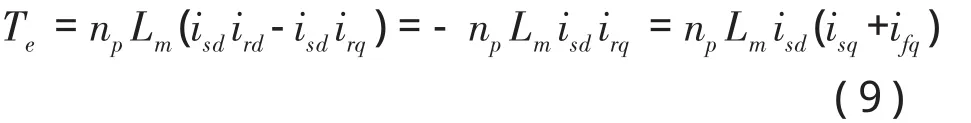
式中，np为电机极对数。

一般ifq与isq比相对很小，可忽略不计，则感应电机的电磁转矩近似为

于是得

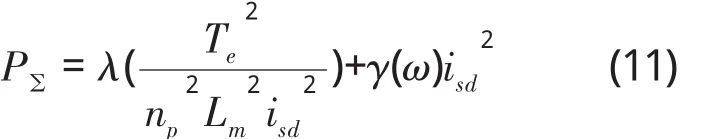
当电磁转矩Te和电机转速ω一定时，求功率损耗对isd的导数并令其为0，得到总损耗最小的关系式

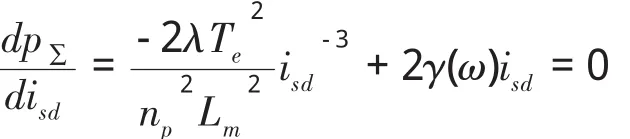
解之，

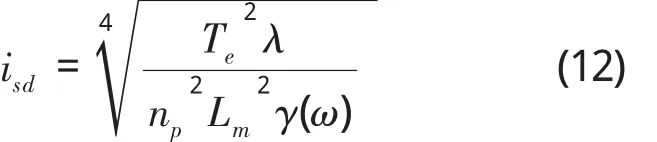
因为转子磁链为

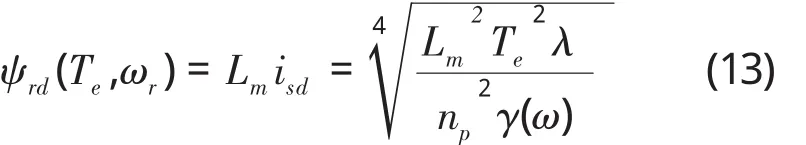
上式即为效率最优控制条件下的定子磁链给定。

在此磁链给定条件下，电机的工作效率为

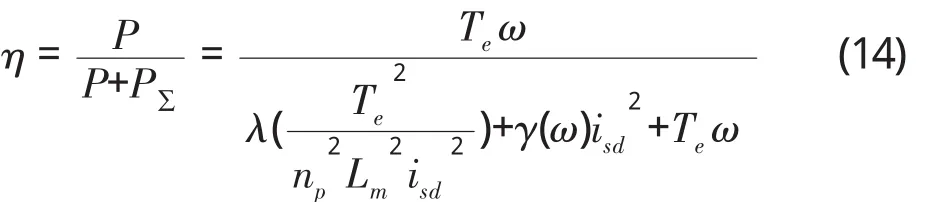
式中，P为电机的输出功率。

3 效率最优控制系统设计

系统采用转子磁场定向矢量控制算法，为实现效率最优控制，在常规的控制模型中加入效率最优化控制模块，该控制模块依据电机的转速反馈和系统的转矩给定，调整定子电流的激磁电流分量isd和力矩电流分量isq，得出定子电流is的给定值，在实现矢量控制的同时，实现效率最优控制。

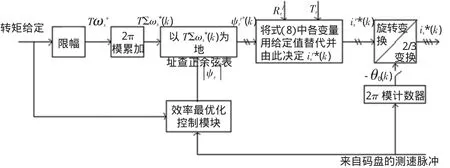
图3 效率最优控制矢量控制系统模型

4 理论计算结果

在实践中，选用了一款6 kW异步电机，参数为

Rs=0.0117 Ω；

Rr=0.0098 Ω；

Lm=0.0018 H；

Rfe=75 Ω；

np=2；

额定转速ω=3000 r/min；

额定转矩Te=19 N·m。

用式（13）和（14）进行计算，计算结果绘制成图，如图4、图5所示。

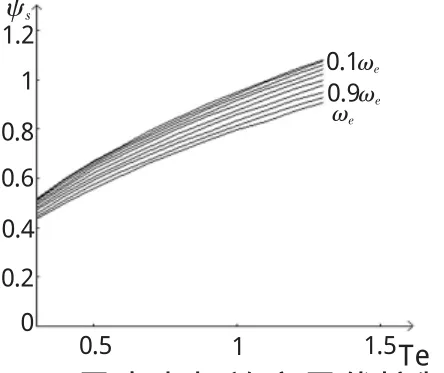
图4 6kW异步电机效率最优控制磁链给定

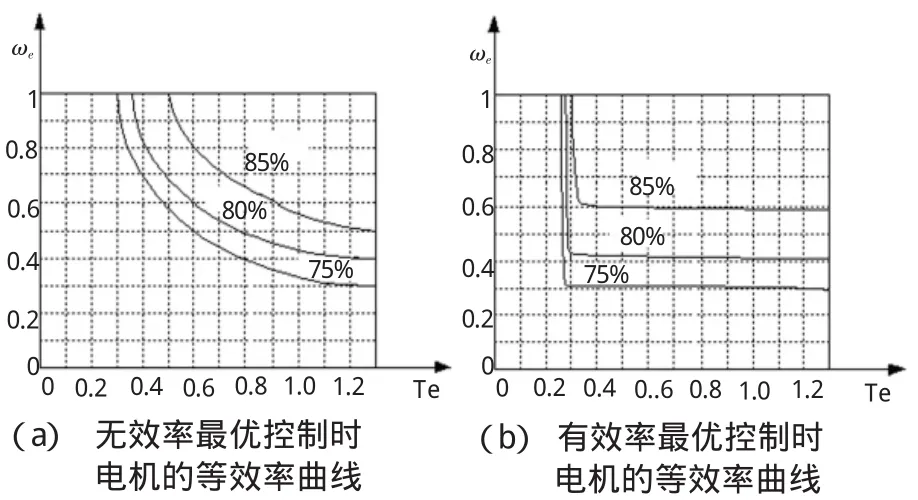
图5 6kW电机高效率运行区的前后比较

从计算结果看出，实施了效率最优控制后，电机在低速轻载运行工况效率有明显的改善，异步电机的高效率运行区域增大，考虑低于75%的效率区域，实施效率最优控制后也有明显改善。

在实施效率最优控制的同时，还应兼顾电机的快速响应性能。在快速的动态响应中，电机的激磁过程比较缓慢，效率最优控制采取的弱磁策略，有可能影响到电机对转矩指令的响应速度，因此激磁给定应设一个下限值，工程实践表明，激磁下限应不低于额定激磁的50%。

5 结束语

本文通过电机的动态模型，推出了电机的稳态模型，并基于稳态模型设计了一种易实现的效率最优控制方法。而实际上的车用电机运行工况非常复杂，所以该方法在电机动态过程的效率最优控制有待于进一步完善。

同时，本文假定电机的定转子参数恒定,假定铁耗与ω无关，这与电机实际运行的状态也有差异，所以采用该方法时，应考虑电机参数变化的控制结果的影响。

[1]陈伯时.电力拖动自动控制系统——运动控制系统（第3版）[M].北京：机械工业出版社，2003.

[2]夏超英.交直流传动系统的自适应控制[M].北京：机械工业出版社，1998.

[3]冯畹芝.电机与电力拖动[M].北京：轻工业出版社，1991.

[4]李海发，王 岩.电机与拖动基础（第3版）[M].北京：清华大学出版社，2005.