永磁电机电磁场的边界元方法

陶瑞民

（新余学院，江西 新余 338031）

与有限元方法相比边界元方法最大的优点是可以降低分析问题的维数，对于拉氏方程，不需要离散整个求解区域，只需对边界进行离散，因此未知数相对减少。边界元方法与有限元方法的区别之一是兼有解析和数值的特点，计算精度高，适合开域场分析。但边界元方法存在奇异积分问题，必须解决这个问题。本文对边界积分方程的建立，边界积分方程的离散和奇异积分的处理及多种材料时边界元方法的处理及应用进行了深入的研究。

1 基本方程

永磁电机的静磁场具有一类和二类边界S1，S2，求解区域D上满足拉氏方程

无限域问题的基本解

式中，r表示电荷集中的作用点（又称源点）P到观测点 Q（又称场点）之间的距离，是场点Q的坐标，（ xp, yp, zp）是源点P的坐标。在区域D内，用加权余量法。以拉式方程的基本解作为权函数，利用高斯积分公式，在边界上得到边界元基本方程。

边界积分方程的推导和积分方程的推导很类似，两者的不同之处只在于需要将源点P移到边界S上。当边界S上的场点Q与源点P趋于接近时，和具有奇异性，这将给问题的求解带来很大的麻烦。为求得良好的计算，必须消除奇异性。为此，需以P点为中心，以ε为半径作球面去掉奇点，具体做法是在三维区域边界上以很小的ε作半球，然后使其半径趋于零，则此点变为边界点。假设边界是S2，且被分成两部分，若已知半球表面积为 2 πε2，令ε→0 ，且φ→φ*，则可得

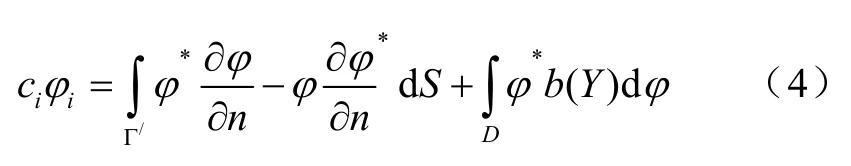
式中，φi是边界上的值。式（4）就是直接边界积分方程。当i点处于光滑表面时， ci= 1 /2；当i点处于不光滑表面时， ci的系数不是1/2，而是与边界上i点所处的立体角有关。

由此可见，奇点本身对积分的贡献已经分离出来，包含在 ciφi项中。式（4）中的面积分不再包含奇点，b为空间电荷量。当b=0时，即为当空间电荷为零时电场满足拉普拉斯方程。

用边界元法对式（4）进行数值计算时，首先对边界进行离散。

将单元上任意点的坐标、电位及电位的方向导数用单元上的局部坐标(ξ ,η)和插值公式来表示，这样就将任意四边形单元变换为边长为2的正方形基单元，如图1所示。对式（4）边界积分方程进行离散，于是有

式中，D(e,l)表示单元e上第l 个节点在N个总体节点编号中的序号，J为雅可比矩阵，l为1到8节点，Nl为插值基函数。由式（5）可以看出积分号中不含未知量，可以经过积分得到确定值。式（5）可以列出N个方程，而每个节点有两个变量，但其中一个是已知的，所以，式（5）成为 N个变量的 N个方程的方程组，用矩阵表示为

离散方程式中，H矩阵和G矩阵的元素中含有二重积分

如果源点P不在当前单元e上，r就不会趋于零，积分无奇异性，可以直接采用高斯积分计算。如果源点P是当前单元e上的某一节点时，积分 l1和 l2就具有奇异性，l1和 l2分别为一阶和二阶奇异积分。这时，应先取消积分奇异性，然后再用高斯积分来计算。

2 处理奇异积分的电位特解法

由上面的分析可见，用传统的边界元方法计算场量时，一个关键而又棘手的问题是奇异积分的处理问题。因此，在边界元方法的研究中，消除奇异性的问题一直是一个重要的研究课题。本文在研究了边界元方程的特点后，采用了一种新的边界元奇异积分的处理方法 电位特解法。

图2 退化单元

积分 l1奇异性的降阶可以通过退化单元来实现。在图2（a）所示奇异单元上，设第1点为奇点，消除奇异性的方法是以此节点为顶点，将奇异单元划成两个三角形单元，如图2（b）所示。把每个三角形都看作是由图2（c）所示的四边形单元退化而成，即三角形单元的奇点是由四边形的一条边退化成的。

在退化单元中，场点Q到源点P的距离r以及雅可比J可用插值公式求得。

对于只有一阶奇异性的积分 用退化单元消除奇异性，再用高斯积分来计算。对于有二阶奇异性的积分 用退化单元还不能消除奇异性。二阶奇异性的积分 l2只出现在 H矩阵的对角线上，因此本文采用电位特解法，由已确定的元素值来推算出对角线上元素。在无外电荷作用下，设

式中，φ0是任意给定的值。将式（9）代入式（6）式得

上式右端是已经确定的矩阵元素。这样不仅确定了H阵中的奇异元素，而且连 ci也不用再单独计算了。

3 计算实例

160kVA永磁电机的结构如图3所示，本文用边界元方法计算了永磁电机的电场,获得了比较满意的结果，图4、图5是永磁电机的磁场分布情况。

图3 160 kW稀土永磁同步发电机三维结构图

图4 磁场沿径向分布

图5 磁场沿角度分布

4 结论

（1）本文用边界元方法计算了永磁电机的磁场，解决了边界元方法中奇异积分问题。

（2）本文的研究对永磁电机的设计起到一定的作用。

[1]B.H.Mcdonaid,A.Wexler “Boundary element solution of unbounded field problems” IEEE Prans. MTT Vo1.mtt 20 pp.841-847,1992.

[2]许强,孙焕纯.厚壳三维分析的虚边界元最小二乘法[J].大连理工大学学报,1996(4).

[3]郭航,冯之鑫,韩朔.轴对称恒定电磁场的标量边界元法[J].电工电能新技术,1994(3).

[4]云玉新,赵笑笑, 罗壬彤等.采用 BEM 计算高压变电站工频电场[J].山东电力技术,2009(5).

[5]刘士利.基于线-面模型的边界元计算特高压交流变电站设备附近工频电场[J].电工技术学报,201(3).

[6]江中和.两种电极结构等离子体发生器的静态电场计算[J].高电压技术,2007,33(9):192-195.

[7]张占龙.多介质工频电场分析的快速多极子边界元法[J].电机与控制学报,2010,14(4):80-85..