基于Fuzzy-PI的BLDCM控制系统的研究
2011-06-22周广旭章松发宋森森李珍国
周广旭 章松发, 宋森森 李珍国
(1.山东省科学院自动化研究所,济南 250014;2.燕山大学,河北 秦皇岛 066004)
永磁无刷直流电机(permanent magnet brushless DC motors,BLDCM)结构简单、功率密度高、调速性能良好,在工业领域中得到了日益广泛的应用[1-3]。
无刷直流电机调速系统快速性、稳定性和鲁棒性的好坏直接决定电机性能优劣的重要指标。BLDCM 是一个高阶、强耦合的系统,有的应用场合对控制系统的要求越来越高,采用传统PI控制方法,难以达到理想的控制效果。因此,本文以数字信号处理器(DSP2812)为核心建立控制平台,主要研究的是基于Fuzzy-PI控制的BLDCM控制系统。
1 无刷直流电机数学模型
本课题电机采用两相导通星形三相六状态,3个霍尔元件在空间相隔120°对称位置。现在建其数学模型,为了满足一般工程的应用,同时又能够抓住无刷直流电机的主要矛盾,则在以上结构基础上,作如下假设以简化分析过程[4-6]:
(l)忽略电机铁心饱和,不计涡流损耗和磁滞损耗。
(2)不计电枢反应,气隙磁场分布近似认为是平顶宽度为120°电角度的梯形波。
(3)忽略齿槽效应,电枢导体连续均匀分布于电枢表面。
(4)驱动系统逆变电路的功率管和续流二极管均具有理想的开关特性。
电机电压平衡方程式
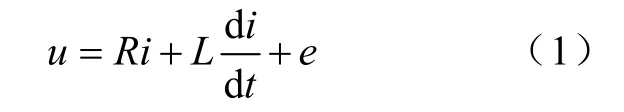
对于三相无刷直流电机,根据上式,可以得到无刷直流电机相电压方程的矩阵形式,如式(2)所示。
电压方程为式(1)
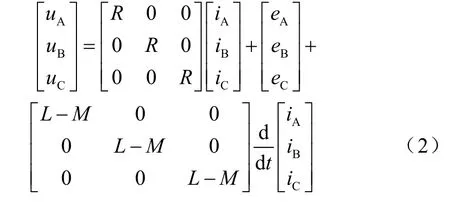
式中,uA, uB, uC为三相定子电压(V);eA,eB,eC为三相定子的反电动势(V);iA, iB, iC为三相定子相电流(A);R为三相定子绕组的相电阻(Ω);L为三相定子自感(H);M为三相定子绕组之间的互感(H);P为微分算子
无刷直流电动机的电磁转矩方程与普通直流电动机相似,其电磁转矩大小与磁通和电流幅值成正比,即

式中, Te为电磁转矩;Ω为电机机械角速度。运动方程

式中,B为黏滞摩擦系数;J为转子转动惯量; TL为负载转矩。
由式(2)的电压方程,可得电机的状态方程为
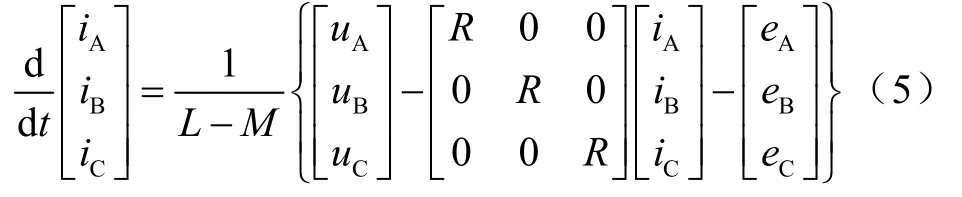
2 Fuzzy-PI控制方法
目前,无刷直流电机的研究和发展取得了长足的进步,但其还有很多需要有待深入研究的主要问题[7]。
转矩脉动、最佳换相、无位置传感器转子位置检测、控制算法、抗干扰等。
无刷直流电机是多变量、非线性、强耦合的系统,使用常规的PI算法难免出现较大的超调、较长的响应时间,而模糊PI控制器的结构是一类被广泛应用的 PI控制器,该控制器改进传统 PI控制器的固定参数 Kp、 Ki的控制策略,提出了可以根据跟踪误差信号等动态改变控制器参数的方法,达到改善控制效果,扩大应用范围的目的。
PI参数模糊自整定是找出 PI两个参数与 E和Ec之间的模糊关系,在运行中通过不断检测E和Ec,根据模糊控制原理对两个参数进行在线修改,以满足不同要求,而使被控对象有良好的动、静态性能。根据参数 Kp、 Ki的作用,在不同的E和Ec下,对PI控制器参数 Kp、 Ki的整定要求如下。
(l)当偏差较大时,为了加快系统的响应速度,应取较大的 Kp;防止出现较大的超调,对积分作用加以限制,通常取 Ki=0。
(2)当偏差处于中等大小时,为使系统响应具有较小的超调, Kp应稍变小, Ki取值要适当。
(3)当偏差较小即接近设定值时,应增加 Kp和减小 Ki的取值,为了避免出现振荡,应增强系统的抗干扰性能[8]。
下列为模糊控制隶属曲线和模糊规则表,如图1和表1所示。

图1 模糊控制的隶属曲线

表1 模糊控制规则表
3 控制策略的研究方案
模糊控制和PI相结合的Fuzzy-PI控制:模糊控制一直是近年来研究的热点,它不依赖于被研究对象精确的数学模型,对系统动态响应有较好的鲁棒性,但难以消除调节终了时系统的稳态误差,而模糊控制和PI相结合的控制方法能很好地解决这一不足。图2所示为系统控制框图。
由于无刷直流电机是多变量、非线性、强耦合的系统,使用常规的PI算法难免出现较大的超调、较长的响应时间。而Fuzzy-PI控制器的结构是一类被广泛应用的PI控制器,该控制器不同于传统的PI控制器的结构参数 Kp、 Ki的控制策略,提出了可以根据跟踪误差信号等动态改变控制器参数的方法,达到改善控制效果,扩大应用范围的目的。

图2 控制框图
4 仿真与实验
以下是无刷直流电机仿真,分别做了电机本体、电流环,传统转速环、Fuzzy-PI转速环等四部分仿真。以下是仿真电机参数如下:
规格型号:92BL430。
额定电压 Ud:310VDC。
额定功率 P2:400W。
额定转速 nN:3000r/min。
额定电流i:1.5A。
最大电流:3.2A。
重量:3.3kg。
4.1 无刷直流电机本体仿真
关于无刷直流电机的本体仿真,速度给定3000r/min,不考虑负载转矩;电压不变,即不做斩波PWM;没有电流环与转速环,即开环。得出的图形有:相电压、相电流,转矩、角位移、反电势等。
仿真分析如下:
由电流波形可以看出,与理想波形几乎一样,额定电流为1.5A,唯有在每相电流导通的120°电角度内,在导通60°电角度后,产生脉动,是由于电机换相时,二极管续流导致而成。相电压的波形与反电势波形相似,只是在换相时,相电压波形上表现出有续流过程,导致中性点电压不同,使相电压产生尖峰值。
额定转矩为1.27N· m,但是在换相时,转矩突变为小于 0.5的值,换相完成,又上升为额定值。角位移的波形是以2π为周期进行变化。反电势波形完全符合无刷直流电机的理想梯形波,幅值为133.33V,为计算值,如图3所示。
4.2 无刷直流电机电流环仿真
本次仿真中,计算端电压的周期是50μs,采用计数的方式来实现,保证开关频率不会高于20kHz。关于相选择:在程序中采用的方式是,在每个扇区中,当某相电流在上一个扇区存在时,被选择与指令电流I进行比较,例如:第一扇区是AB相导通,选择ib,因为在第六扇区CB导通时,ib存在,此时电流差为I-ib。依此类推其他扇区。当ωc选取5000rad/s时, Kp= 6 .61,Ki= 79351。仿真结果见图 3-图 4。

图3 相电压、相电流、转矩、角位移和反电势的波形

图4 三相电流、PI输出电压、转矩、反电势的波形
仿真分析如下:
由于加了电流环,端电压每 50μs运算更新一次,所以转矩的波形与本体时的波形相比,也有很大差别。在指令电流发生突变时,从1.5A变为1.0A,再变为1.5A,在电流环的调节下,电流随即变化,使转矩得到明显的调节,达到设计电流环的目的。随着指令电流的变化,使电流差产生变化,引起PI输出的变化,最终使电机的端电压发生变化。在每次换相时,实际电流会有大的波动,导致电流误差变大,所以u在每次换相时,都有明显的脉动。从电流波形可知,加了电流环后,电流的波形没有本体仿真的波形平滑,因为在换相后,电流须上升到指令值,通过PI调节作用,所以存在超调。电流的波动,引起转矩也存在超调现象。从波形上可以看到,实际电流的变化的效果也很明显,由此可体现PI控制器的调节作用,如图4所示。
4.3 无刷直流电机传统转速环仿真
关于无刷直流电机的转速环仿真,在电流环的基础上加上PI转速控制器,即转速控制系统,仿真结果见图5。

图5 转速、三相电流、PI输出端电压、转矩、反电势波形
仿真分析如下:
从图5可以看出,电机从起动开始,反电势e由0升到133.33V,电流i以3.2A作为限幅值。当电机启动完成,反电势为 133.33V,电流的幅值保持为额定值1.5A内。在0.18s时,将指令转速n从3000r/min突变为 2000r/min,反电势开始下降,电流变得很小,并有波动,图中看的不是很明显。当实际转速n1降到2000r/min时,反电势不再减小,电流恢复到幅值为1.5A的范围内波动。同理,指令转速n从2000r/min突变为1000r/min时,反电势与电流的变化同上。
电机起动过程,指令转速n为3000r/min,在转速环PI调节器的作用下,角速度的差值,引起指令电流的变化,从而使电流差值变化。在电流环PI调节器的作用下,端电压的积分量在变化,使端电压从0开始上升,起动电流大,使起动转矩也大,使实际转速从0开始上升。当实际转速达到指令转速时,电机启动完成,端电压持平,电磁转矩变为幅值为1.27N·m的范围内波动。在指令转速突变为 1500r/min时,电流变化,端电压积分量变化,端电压也随之变化,转矩下降,实际转速下降为1500r/min,如图5所示。
4.4 无刷直流电机Fuzzy-PI转速环仿真
采用Fuzzy-PI控制的转速环,反电势、三相电流波形,转速、转矩、端电压波形,仿真结果与传统控制的仿真结果类似。主要需要说明的是转速波形的区别,具体波形与分析,在下一部分进行详细说明。
4.5 传统PI与Fuzzy-PI转速环仿真结果比较
为了使对比更加明显,将波形进行放大处理。
如图6所示,给出传统PI的转速波形,此处将转速调到1000r/min,可以在0.055s时,看到有明显的超调存在,为一个超出额定值15的峰值。
如图7所示,为Fuzzy-PI控制转速环的转速波形,与传统转速环的转速波形相比,稳态性能变好,没有超调,具有较好的鲁棒性。这是单纯的PI控制难以实现的。从响应时间上比较,比传统的快了0.001s。
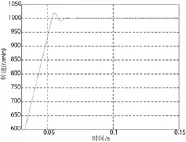
图6 传统PI转速波形
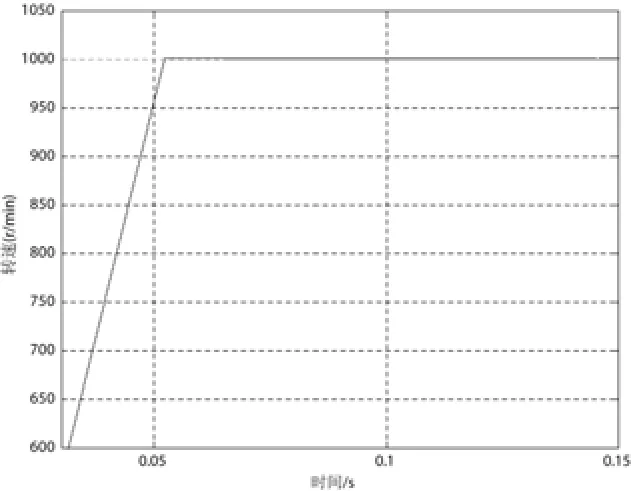
图7 Fuzzy-PI转速波形
4.6 仿真与试验对比
如图8所示,列出的是B相电流、C相电流,还有AB间线电压仿真波形。

图8 B相电流、C相电流、AB间线电压仿真波形
如图9所示,列出的是B相电流、C相电流,还有AB间线电压实验波形。
对比仿真与实验波形,理论与实际是相符的。
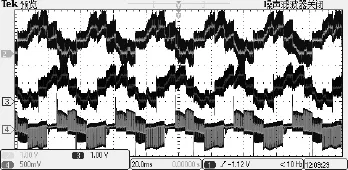
图9 B相电流、C相电流、AB间线电压实验波形如图10所示,为三路霍尔位置信号波形。霍尔位置信号交替输出有一个宽为180°电角、相伴互差120°电角的矩形波信号。

图10 三路霍尔位置信号波形
如图11所示,为A、B相上下桥臂的PWM波形,方式是H_PWM-L_ON,低电平有效。

图11 A、B相上下桥臂PWM波形
5 结论
无刷直流电机具有输出转矩大、调速性能好、运行可靠等一系列优点,具有广泛的应用前景。同时,BLDCM又是一个非线性系统,致使传统的PI控制难以满足高的控制要求,促使Fuzzy-PI控制得到应用。仿真和实验结果表明,本文所做工作是具有意义的。
[1]夏长亮,李正军,杨荣,等.基于自抗扰控制器的无刷直流电机控制系统[J].中国电机工程学报,2005,25(2):82-86.
[2]夏长亮,郭培健,史婷娜,等.基于模糊遗传算法的无刷直流电机的自适应控制[J].中国电机工程学报,2005,25(11): 129-133.
[3]夏长亮,刘均华,俞卫,等.基于扩张状态观测器的永磁无刷直流电机滑模变结构控制[J].中国电机工程学报,2006,26(20):139-143.
[4]Krause P C. Analysis of Electric Machinery. Kinsport Town: Kinsport Press Inc.,1986.
[5]Pillay P, Krishnan R. Modeling, simulation, and analysis of permanent-magnet motor drives, part II:The brushless DC motor drive. IEEE Transactions on Industry Application, 1989, 25(2):274-279.
[6]Pillay P, Krishnan R. Modeling, simulation, and analysis of permanent-magnet motor drives, part I: The brushless DC motor drive. IEEE Transactions on Industry Application,1989,25(2):265-273.
[7]罗隆福,杨艳,方日杰.无刷直流电动机中有待深入研究的主要问题[J].微电机,2002(1).15-16.
[8]卢旭.电动汽车驱动控制系统的研究与设计[D].长安大学,2007.
