加筋土筋材拉伸力学特性与模型分析

林宇亮，杨果林，刘冬

(中南大学 土木工程学院，湖南 长沙，410075)

加筋土筋材被誉为“继钢筋混凝土之后又一造福于人类的复合材料”。目前，加筋土结构已经得到了广泛研究和推广[1-5]。加筋土筋材的拉伸力学特性是加筋土结构设计最基本的技术指标，筋材的应力应变特性直接影响到加筋体的侧向位移、竖向沉降、安全使用寿命等[6]。国内外一些单位和学者对加筋土筋材的拉伸力学特性开展了一定的研究，如：杨果林等[6]研究了土工带、土工布、土工格栅和土工网等4种筋材在循环荷载作用下的应力应变特性；Masahiro Shinoda等[7]研究了3种土工格栅(PET, PP和HDPE)在拉伸力作用下的竖向和侧向变形特性；Boisse等[8-9]进行了材料的双向拉伸试验。很多学者也研究了拉伸速率、试件尺寸等因素对拉伸试验结果的影响[7,10-12]。Perkins[13]建立了加筋土筋材的本构关系，并通过一系列拉伸试验进行了对比验证。尽管如此，不同筋材的力学特性相别很大，具体的拉伸力学特性还须采用拉伸试验来确定。另一方面，采用不同的力学模型来模拟筋材的力学特性，确定合适的力学模型，从而进一步揭示筋材的内部变形特性，是一个值得研究的课题[14-15]，然而，这方面的研究成果却并不多见。鉴于此，本文作者以湖南省湘潭至衡阳高速公路加筋土实体工程为依托背景，选取MAC土工格栅、70RE和80RE土工格栅、格宾金属丝(直径2.7 mm)、金属丝直径为2.2 mm和2.7 mm格宾网(网孔型号80 mm×100 mm)、金属丝直径为2.2 mm格宾网(网孔型号60 mm×80 mm)、无PVC包裹金属丝直径为2.7 mm格宾网(网孔型号80 mm×100 mm)等筋材进行拉伸试验(文中未特别注明的均指有PVC包裹层的格宾网)，得到了这些筋材的拉伸力学特性，并采用标准线性三元件模型、非线性三元件模型和 Kawabata 改进模型对筋材拉伸曲线进行了模拟。其中，MAC土工格栅、格宾网等在国内为新型的加筋土材料，格宾结构以其良好的工程特性和价格优势在公路工程、铁路工程、市政工程以及5.12汶川特大地震灾后重建等工程项目中得到了很快的推广和应用。

1 试验概况

格宾金属丝(直径2.7 mm)拉伸试验也在拉伸试验机上进行，共进行了6组平行试验。为减少夹具给格宾金属丝带来的应力集中现象，在夹持处外裹土工布。

70RE和80RE土工格栅拉伸试验采用了4片专门的夹具，并采用 MTS施加拉伸荷载。筋材的一端固定在2片夹具上，并通过夹具固定在底下的横梁上，不会发生竖向和水平位移；另一端通过另外2片夹具固定在MTS作动器上。70RE和80RE土工格栅各进行了5组平行试验。

格宾网为双绞合六边形。各种型号和尺寸的格宾网的拉伸试验也采用夹具固定，并通过 MTS施加拉伸荷载。夹具有2排不同尺寸的横向夹孔，能应用于网孔型号分别为80 mm×100 mm和60 mm×80 mm的格宾网。格宾网的网孔紧紧地有序地固定在2片夹具的夹孔上，夹具的两端有2个侧向夹孔(A和B，如图1所示)，能有效地限制试件夹持处的横向变形。

对金属丝直径为 2.2 mm和 2.7 mm的格宾网(80 mm×100 mm)分别进行了2种几何尺寸的拉伸试验，5～6组平行试验，共计试验22次。对2.2 mm格宾网(60 mm×80 mm)进行了5组平行试验。对无PVC包裹层的金属丝直径为 2.7 mm格宾网(80 mm×100 mm)进行了2组平行试验。

图1 格宾网的夹持方式(单位：mm)Fig.1 Clamping method for gabion mesh

试验均在常温下进行，单位时间(每分钟)的拉伸长度为20%l，其中，l为名义夹持长度。试验中各组平行试验结果离散性小。

2 试验结果与分析

2.1 筋材拉伸试验结果与分析

MAC土工格栅为片状结构，拉伸试验选取单片土工格栅，共进行了6组平行试验。试验在100 t位的拉伸机上进行。为减少锲形夹具对筋材的损伤，在夹持处筋材外裹土工布。试验中，筋材一端固定，另一端匀速张拉，筋材受力均匀，且拉伸过程中筋材没有发生滑移。

每种筋材试验结果平均值如表1所示。筋材拉伸实验曲线和破坏形式分别如图2和图3所示。

单片 MAC土工格栅的典型拉伸曲线如图 2(a)所示，其破坏形式如图 3(a)所示。由于单片土工格栅所占的宽度为116 cm，因此，可以推算出MAC土工格栅的拉伸力学参数(如表1所示)。从表1可以看出：单片MAC土工格栅的拉伸曲线并没有出现明显的屈服阶段，当弹性变形达到一定程度直接发生破坏，之后抗拉强度迅速下降。单片MAC土工格栅可以承受58.1 kN的力，经换算后MAC土工格栅抗拉强度高达501.2 kN/m，表现出显著的高强度特性。

70RE和80RE土工格栅(以下简称土工格栅)拉伸曲线如图2(b)所示。土工格栅破坏形式如图3(b)所示。可以看出：土工格栅的拉伸曲线出现了弹性阶段、屈服强化阶段以及软化阶段；在拉伸荷载作用下，土工格栅的破坏模式为多条筋肋同时崩断，断裂后拉力发生突变并迅速降为0 kN。

格宾金属丝(直径 2.7 mm)的典型拉伸曲线如图2(c)所示。可见：格宾金属丝在较小的应变下就出现了屈服现象，其应力应变曲线呈现出很长的屈服台阶。试验中格宾金属丝均在中间位置发生断裂。

格宾网拉伸曲线如图2(d)所示。格宾网的破坏形式通常表现为六边形网孔中斜向网丝发生断裂(如图3(c)所示)。结合表1可以看出：格宾网发生网丝断裂前没有出现明显的屈服阶段，格宾网断裂形式为网丝逐条断裂，拉伸曲线呈现出锯齿状，有别于土工格栅多条筋肋同时崩断的现象。对比直径为2.7 mm和2.2 mm格宾网(80 mm×100 mm)的试验结果发现：几何尺寸影响筋材最大负荷下伸长率的试验结果，试件尺寸越长，最大负荷伸长率越小，对筋材的拉伸强度影响不显著；PVC包裹层对格宾网的抗拉强度影响不大；PVC包裹层主要作用为防腐，增加筋材的使用寿命；不同的网孔型号(60 mm×80 mm和80 mm×100 mm)格宾网拉伸力学性能差别较大，小型号格宾网由于格宾网丝较为密集，其拉伸强度大于大型号格宾网的拉伸强度。

2.2 筋材受力集中情况

单片MAC土工格栅在拉伸荷载作用下发生整片屈服破坏，70RE和80RE土工格栅为多条筋肋同时崩断的破坏现象，因此，它们在拉伸荷载作用下可以认为受力均匀。

拉伸试验中格宾网破坏形式为网丝逐条断裂。尽管如此，从格宾金属丝(直径为2.7 mm)的拉伸曲线(图2(c))可以看出：格宾金属丝在小应变时就具有较高的抗拉强度，且呈现出很长的屈服台阶。因此，格宾网在产生了一定的拉伸变形之后，能很好地调整格宾网丝的受力状况，使每一根格宾网丝都具有较高的抗拉强度。

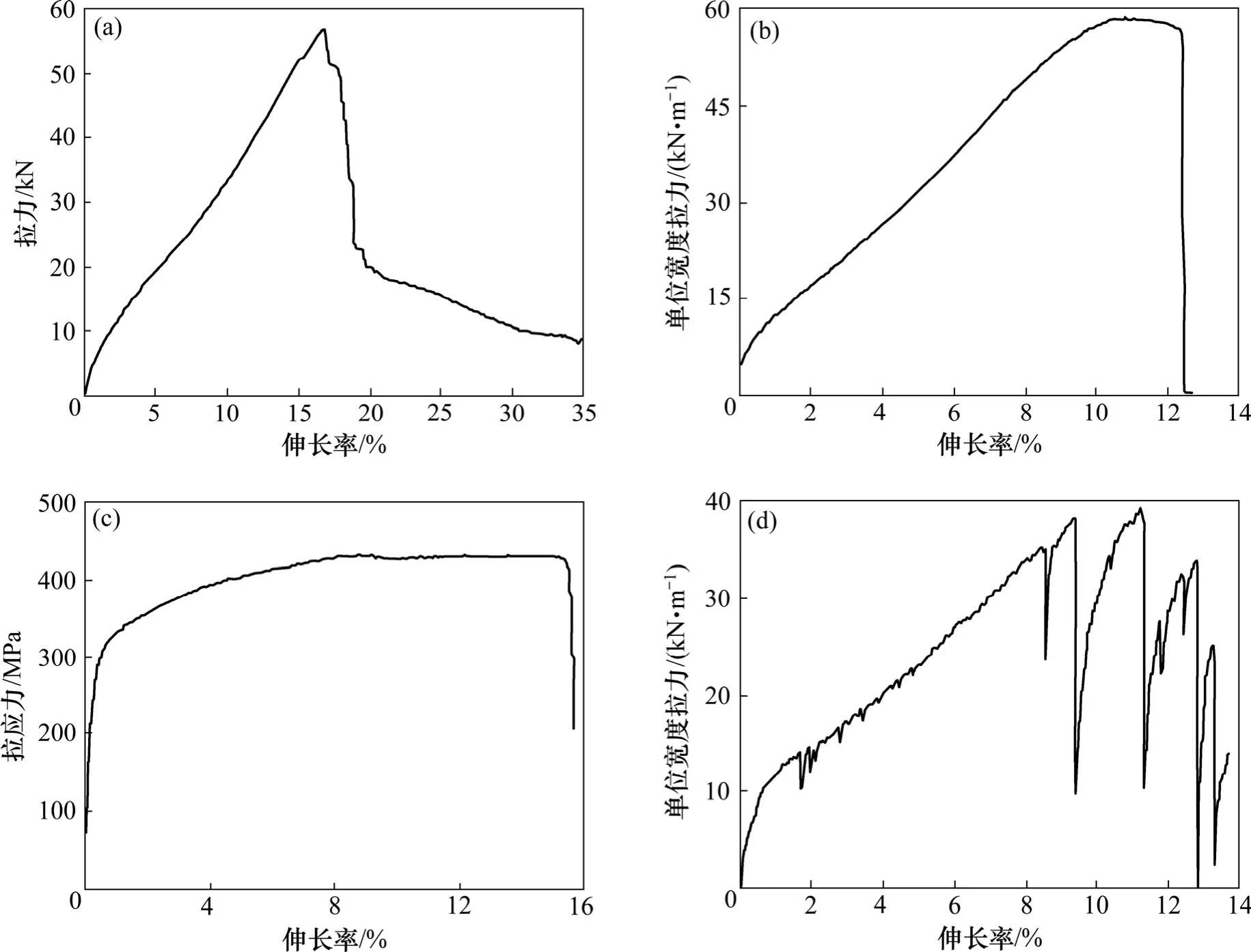
图2 筋材拉伸试验典型曲线Fig.2 Typical tensile curves of reinforcements

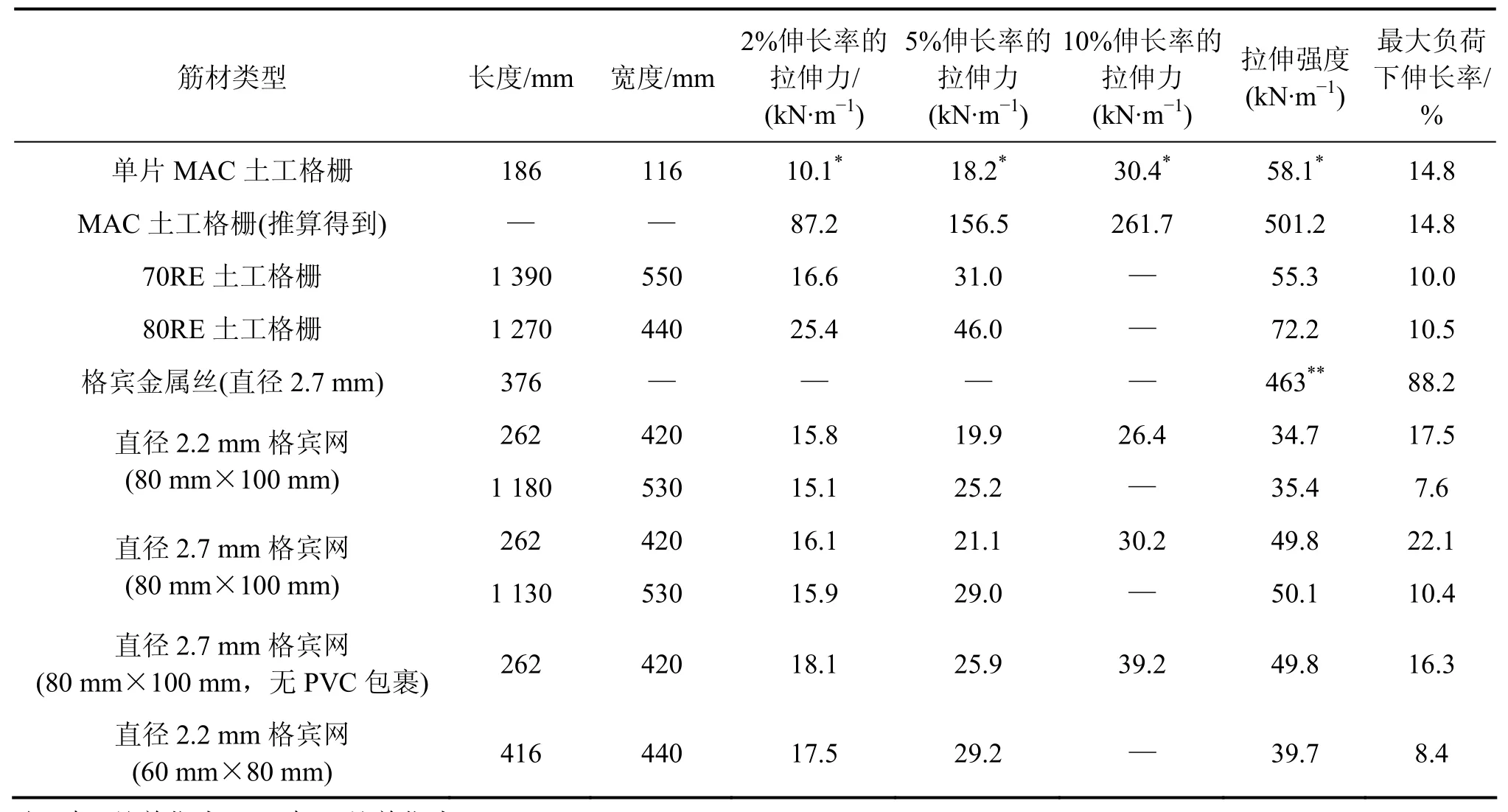
表1 筋材主要力学性能指标的拉伸试验结果Table 1 Main mechanical indexes of reinforcements based on tensile test

图3 筋材的破坏形式Fig.3 Failure modes of reinforcements

为定量描述格宾网受力集中情况，定义受力集中系数K：

其中：T0为按格宾金属丝抗拉强度换算得到的格宾网单位宽度拉伸强度，kN/m；T为试验得到的格宾网单位宽度拉伸强度，kN/m。受力集中系数K越大，格宾网受力集中现象越严重。

以网孔型号为80 mm×100 mm、直径为2.7 mm格宾网为例，其抗拉强度为f=463 MPa，因此，每根格宾金属丝能承受的拉力为F=2.648 kN。网孔型号80 mm×100 mm的格宾网的网丝密度为ρ=25根/m，由此可得：T0=F·ρ=66.2 kN/m。由拉伸试验得到的T=49.8 kN/m，将T0和T代入式(1)可求得K=1.33。在上述计算中，计算T0时并没有考虑格宾网中斜向网丝给拉伸强度带来的折减，这样将使得T0偏大，K也偏大。由此可见：格宾网在拉伸荷载作用下能很好地调整格宾网丝的受力状况，不会产生很大的受力集中现象。

2.3 格宾伸长率计算方法探讨

格宾网在拉伸荷载作用下还会产生一定的横向变形，即颈缩现象。在对格宾网伸长率计算时作如下假定：(1) 拉伸荷载均匀地分布在每根格宾网丝上，拉伸过程格宾网始终保持为一平面；(2) 不考虑格宾网的边界影响；(3) 不考虑颈缩现象和格宾网丝屈服变形引起的双绞合六边形的畸变。

根据以上假定，选取其中1个六边形网孔单元，并对结点作受力分析，如图4所示。格宾网拉伸变形量Δl由 2部分构成：六边形网孔中双绞合网丝(如图4(a)中的AB段)引起的变形量Δl1和斜向网丝(如图4(a)中的BC段)产生的变形量Δl2。即：

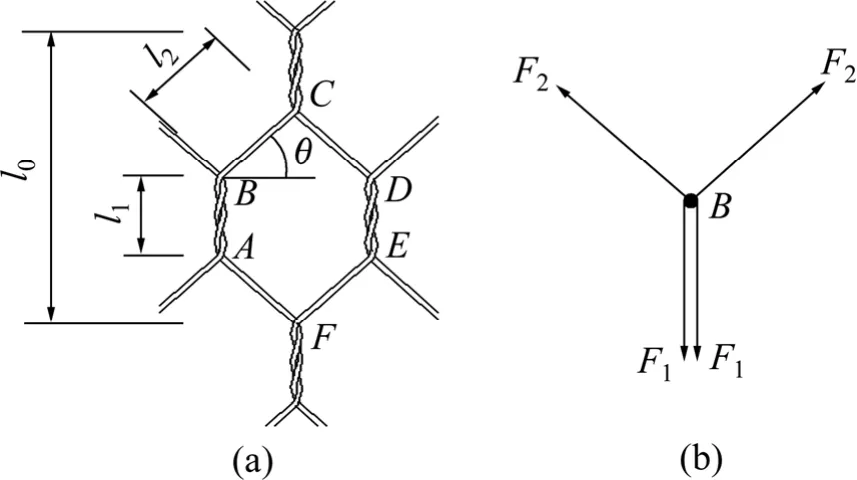
图4 格宾伸长率计算示意图Fig.4 Schematic diagram for unit elongation calculation of gabion mesh

而

式中：A为网丝的截面面积；E为网丝的割线变形模量；n为某一长度格宾网沿拉伸方向具有六边形单元的个数。设格宾网长为l，1个六边形单元拉伸方向长为l0，则有：

则格宾网的伸长率ε为：

对结点作受力平衡分析，有

由于θsin≤1，六边形网孔中斜向网丝将率先达到破坏强度，即 F2=Fb，这与拉伸试验中格宾网通常表现为六边形斜向网丝发生断裂破坏的结论一致。此时有F1= Fb·sin θ 。将其代入式(6)可得：

其中：l0，l1，l2和θ取决于格宾网六边形的形状特点。由此可知：格宾网的伸长率取决于六边形网孔的形状特点、格宾网丝的截面面积、割线变形模量、破坏强度等参数。

3 拉伸曲线模拟

确定能描述筋材力学特性的合理力学模型，对研究筋材内部变形具有重要意义。本文选取标准线性三元件模型、非线性三元件模型和 Kawabata 改进模型[14-17]分别对筋材拉伸曲线进行模拟。

3.1 模型简介

3.1.1 线性与非线性三元件模型

标准线性三元件模型由Maxwell体和胡克型弹簧体并联而成；非线性三元件模型由Maxwell体和非线性弹簧体 σ =bε2(其中，σ为应力，b为参数)并联而成，如图5所示。由此可求解这2种模型的本构关系。

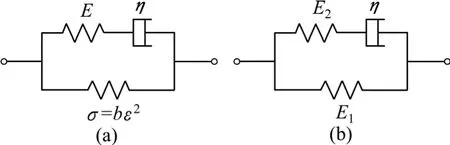
图5 线性与非线性力学模型Fig.5 Linear and nonlinear model

线性模型为：

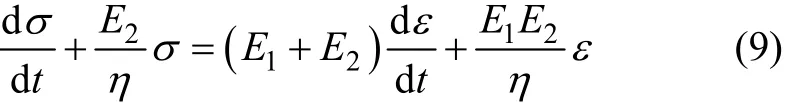
非线性模型为：

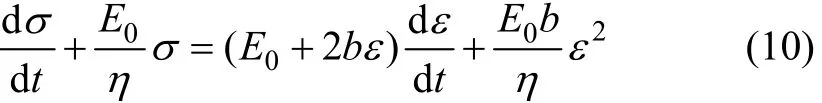
式中：E0，E1，E2和η均为模型参数。

当等速拉伸时，应变ε与时间t成正比，即ktε=(k为常数)。将ktε=分别代入式(9)和(10)，并由初始条件(即当时间t=0时，初应力00σ=)求解微分方程，可得到2种模型的应力应变公式。

线性模型为：

非线性模型为：

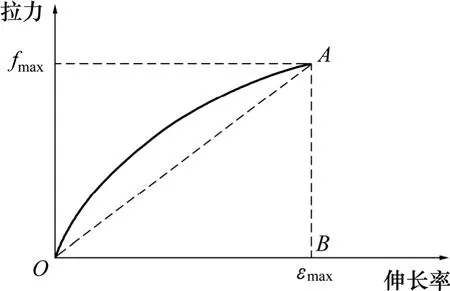
图6 Kawabata改进模型计算示意图Fig.6 Schematic diagram for calculation of Kawabata improved model

3.1.2 Kawabata改进模型

Kawabata改进模型的拉伸力为：

其中：fmax为最大应变(断裂伸长率)所对应的应力；Wt为单位面积的抗拉能，其值等于筋材拉伸曲线与横轴所围成的面积；Lt为拉伸线性比，其值为Wt与三角形OAB面积之比：当拉伸曲线向上凸时，Lt＞1；反之，Lt＜1，如图6所示。

3.2 拉伸曲线模拟与分析

针对不同的筋材类型，分别选取单片MAC土工格栅、70RE土工格栅、格宾金属丝和直径为2.2 mm格宾网(80 mm×100 mm)进行典型分析，并只对筋材发生破坏前的拉伸曲线进行模拟。采用线性模型和非线性模型进行拉伸曲线模拟时，对应式(11)和(12)为非线性回归问题，根据最小二乘法可求得3种模型的拟合参数，结果如表2～4所示。4种筋材的拉伸曲线模拟情况及残差分布如图7～10所示。

对于单片MAC土工格栅，3种模型与实测曲线的模拟效果均非常好。模拟效果最优为非线性模型。其次为标准线性模型，最差为Kawabata改进模型。

对于70RE土工格栅，非线性模型和标准线性模型的模拟结果非常接近。3种模型均难以模拟土工格栅拉伸曲线出现峰值前后变化的情况，无法反映土工格栅断裂前应力减小软化的特征。非线性模型和标准线性模型的模拟断裂点高于实测点，而Kawabata改进模型则低于实测点。

对于格宾金属丝，非线性模型和标准线性模型的模拟效果比较好，其中，标准线性模型略优于非线性模型。Kawabata改进模型的模拟效果比较差，Kawabata改进模型无法模拟格宾金属丝拉伸曲线小应变屈服、长屈服台阶的特征。

对于直径为2.2 mm格宾网，非线性模型和标准线性模型具有较好的模拟效果，Kawabata改进模型次之。3种模型均无法模拟格宾网拉伸曲线锯齿状的特点。

表2 单片MAC土工格栅的模拟参数Table 2 Simulation parameters of MAC geogrid

表3 土工格栅和2.2 mm格宾网的模拟参数Table 3 Simulation parameters of geogrid and 2.2 mm gabion mesh

表4 格宾金属丝的模拟参数Table 4 Simulation parameters of gabion wire

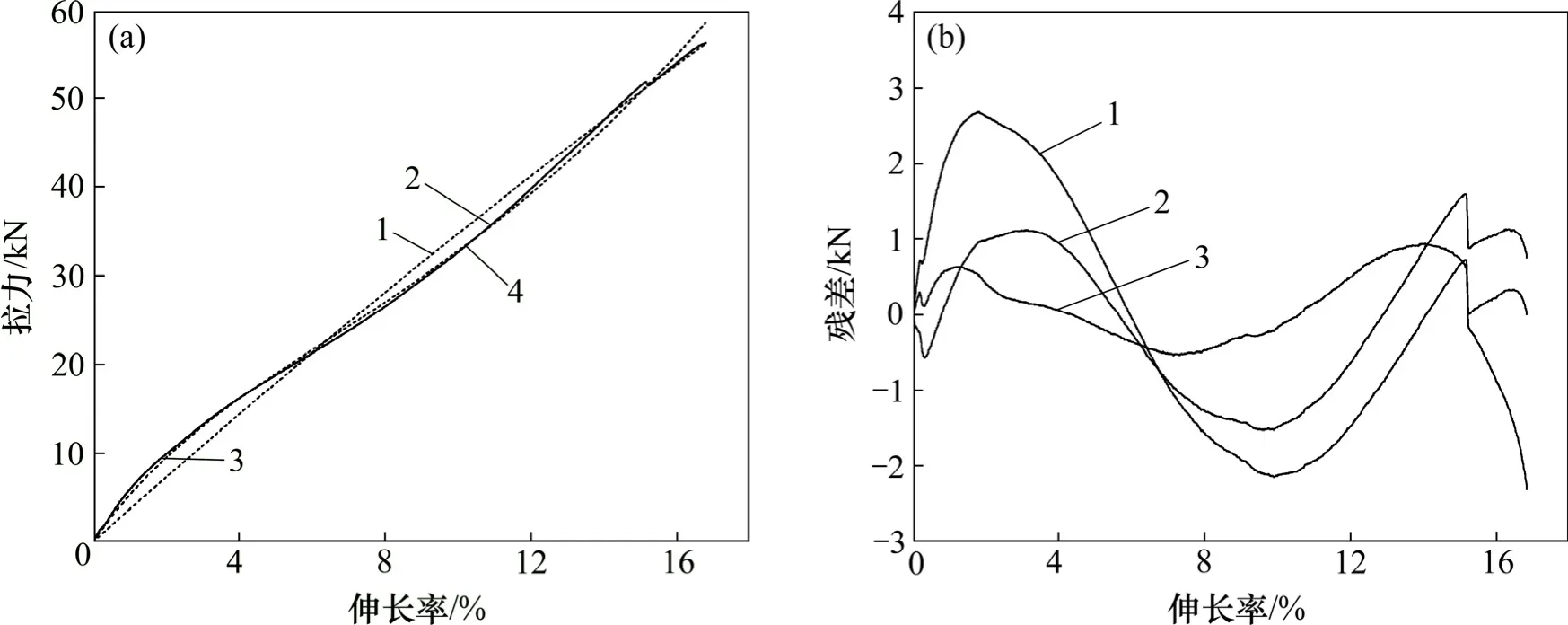
图7 MAC土工格栅拉伸曲线模拟与残差分析Fig.7 Tensile curves simulation and residual analysis of MAC geogrid

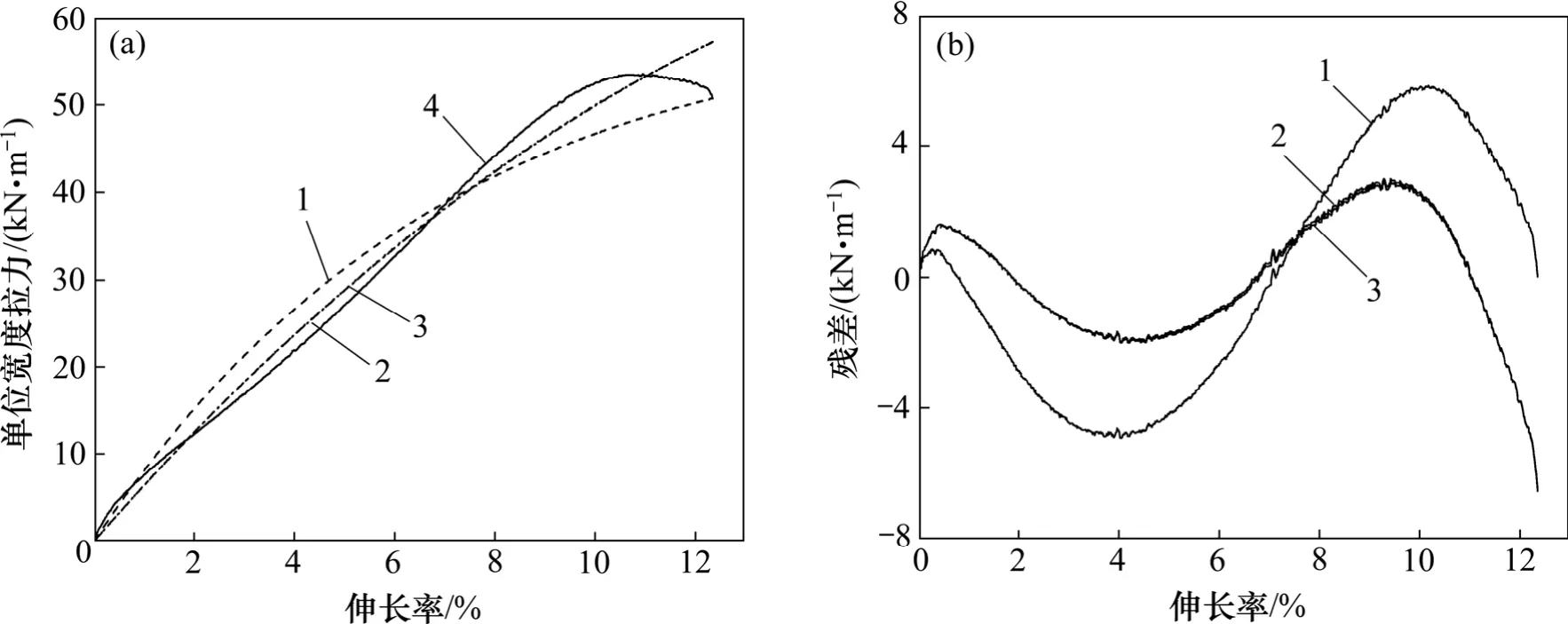
图8 土工格栅拉伸曲线模拟与残差分析Fig.8 Tensile curves simulation and residual analysis of geogrid

3.3 讨论

对不同的力学模型模拟效果进行比较，选取合适的力学模型，并考虑力学模型各参数的变化情况，对进一步研究筋材的内部变形特点具有重要的意义。如对于标准或非线性三元件模型的Maxwell单元体，若η越大，则表示筋材弹性增加，若η→∞，则模型完全呈现胡克弹性体的变形特性。因此，η反映了黏性流动单元的变形，η越小，表示流动变形能力大。能否对加筋土筋材的力学特性研究上升到微观角度，揭示筋材内部分子变形机理，有待于进一步的探讨。

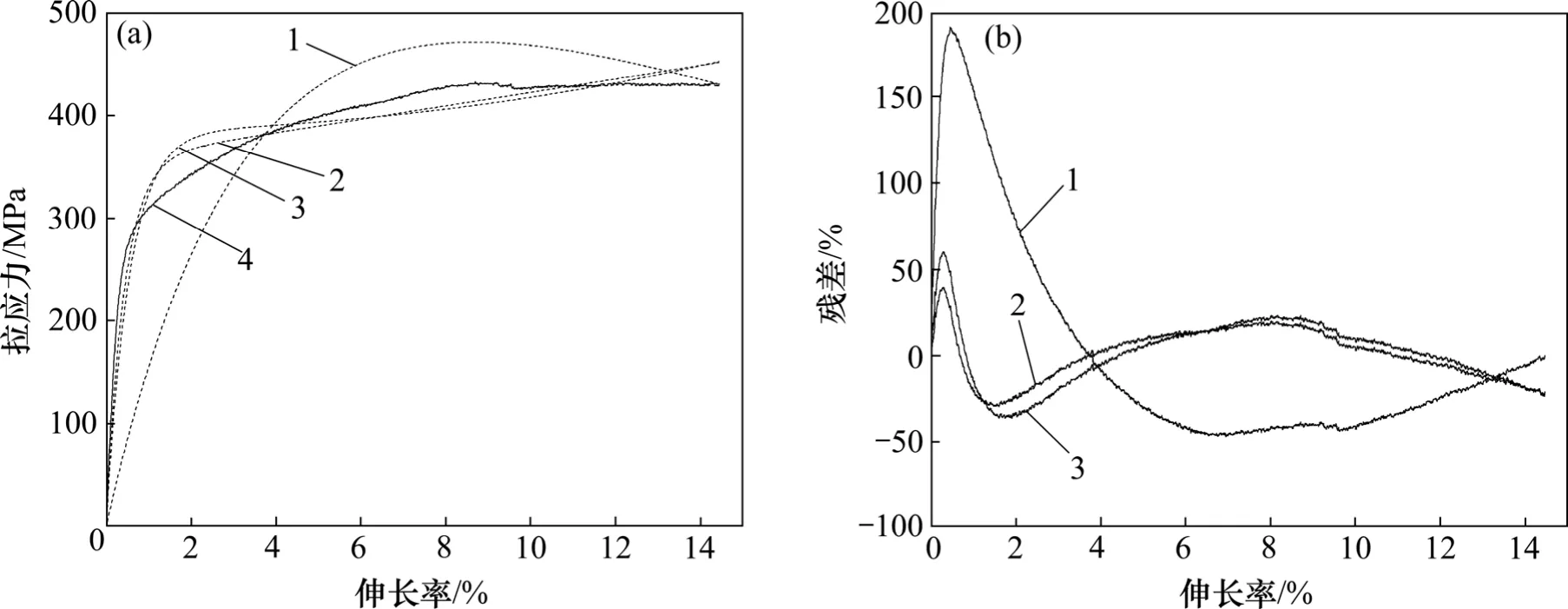
图9 格宾金属丝拉伸曲线模拟与残差分析Fig.9 Tensile curves simulation and residual analysis of gabion wire

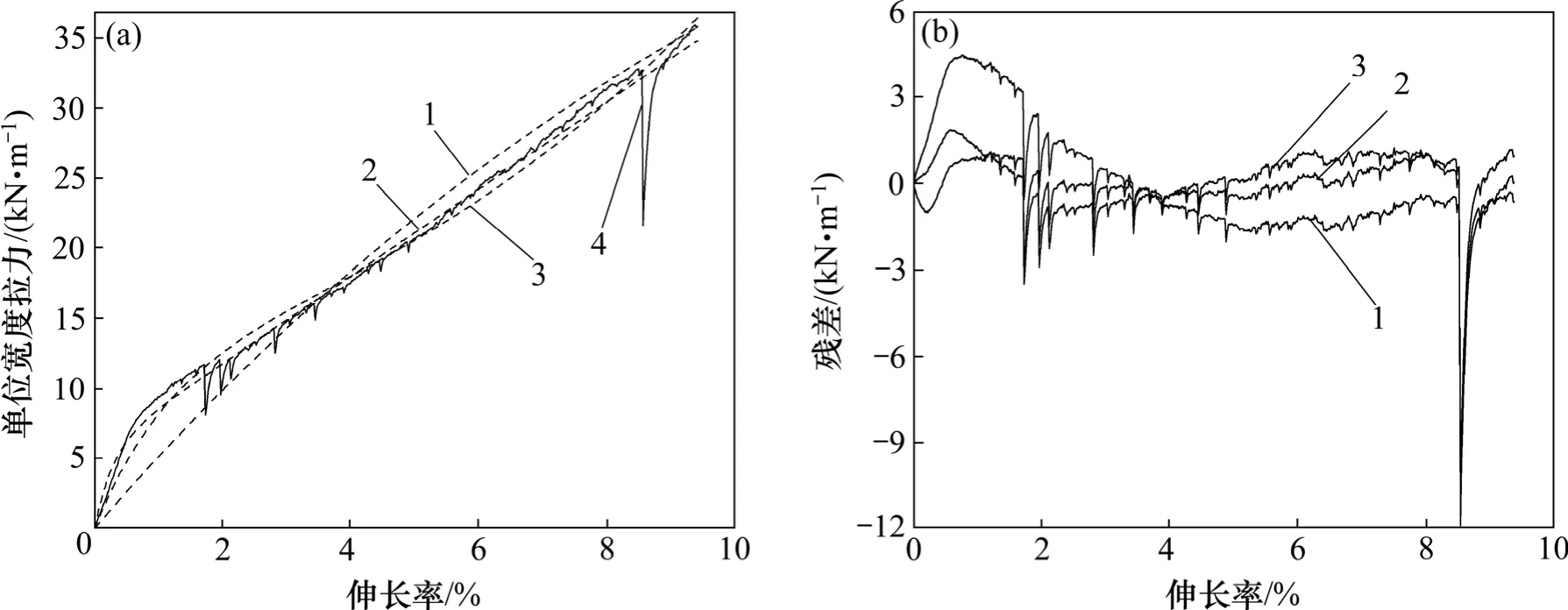
图10 格宾网拉伸曲线模拟与残差分析Fig.10 Tensile curves simulation and residual analysis of gabion mesh

4 结论

(1) 本文所采用的夹具能很好地夹持宽带土工格栅和格宾网，取得了较好的试验效果。

(2) MAC土工格栅表现出显著的高强度特性。70RE和80RE土工格栅的拉伸曲线都出现了线弹性阶段、屈服阶段和软化阶段。其破坏模式为多条筋肋同时崩断。

(3) 格宾金属丝为小应变屈服，且呈现出长屈服台阶。格宾网拉伸曲线呈现出锯齿状，PVC包裹层对其抗拉强度影响不大。不同型号的格宾网拉伸力学性能指标差别较大。

(4) 格宾网在拉伸荷载作用下能较好地调整网丝的受力状况，不会产生很大的受力集中现象。

(5) 格宾网的伸长率取决于六边形网孔的形状特点、格宾网丝的截面面积、割线变形模量、破坏强度等参数。

(6) 标准线性三元件模型、非线性三元件模型对MAC土工格栅、格宾网金属丝和格宾网模拟效果良好，Kawabata 改进模型对MAC土工格栅模拟效果良好。对于70RE土工格栅3种模型模拟效果不佳。

[1] Quang T S, Ghazi H, de Patrick B. A multiphase approach to the stability analysis of reinforced earth structures accounting for a soil-strip failure condition[J]. Computers and Geotechnics, 2009,36(3): 454-462.

[2] ZHANG Ling, ZHAO Ming-hua, HE Wei. Working mechanism of two-direction reinforced composite foundation[J]. Journal of Central South University of Technology, 2007, 14(4): 589-594.

[3] Zhang M X, Zhou H, Javadi A A, et al. Experimental and theoretical investigation of strength of soil reinforced with multi-layer horizontal-vertical orthogonal elements[J].Geotextiles and Geomembranes, 2008, 26(1): 1-13.

[4] Viswanadham B V S, Konig D. Centrifuge modeling of geotextile-reinforced slopes subjected to differential settlements[J]. Geotextiles and Geomembranes, 2009, 27(2):77-88.

[5] 李献民, 王永和, 律文田, 等. 土工格栅加固路桥过渡段的动测试分析[J]. 中南大学学报: 自然科学版, 2004, 35(4):860-864.LI Xian-min, WANG Yong-he, LÜ Wen-tian, et al. Dynamic test analysis on roadbed-bridge transition section reinforced by geogrid[J]. Journal of Central South University: Science and Technology, 2004, 35(5): 860-864.

[6] 杨果林, 王永和. 土工合成材料在加卸循环荷载作用下的应力应变特性研究[J]. 铁道学报, 2002, 24(3): 74-77.YANG Guo-lin, WANG Yong-he. Study on stress-strain relationship of geosynthetics under cyclic loaded-unloaded[J].Journal of the China Railway Society, 2002, 24(3): 74-77.

[7] Masahiro S, Rrchard J B. Lateral and axial deformation of PP,HDPE and PET geogrids under tensile load[J]. Geotextiles and Geomembranes, 2004, 22(4): 205-222.

[8] Boisse P, Gasser A, Hivet G. Analyses of fabric tensile behaviour: Determination of the biaxial tension-strain surfaces and their use in forming simulations[J]. Composites Part A, 2001,32(10): 1395-1414.

[9] Buet-gautier K, Boisse P. Experimental analysis and modeling of biaxial mechanical behavior of woven composite reinforcements[J]. Experimental Mechanics, 2001, 41(3):260-269.

[10] 李俊伟, 黄宏伟. 土工格室 HDPE片材拉伸应变率相关特性[J]. 建筑材料学报, 2008, 11(2): 47-51.LI Jun-wei, HUANG Hong-wei. Strain rate dependent tensile behavior of HDPE geocell strip[J]. Journal of Building Materials,2008, 11(2): 47-51.

[11] Wesseloo J, Visser A T, Rust E. A mathematical model for the strain-rate dependent stress-strain response of HDPE geomembranes[J]. Geotextiles and Geomembranes, 2004, 22(4):273-295.

[12] Subaida E A, Chandrakaran S, Sankar N. Experimental investigations on tensile and pullout behaviour of woven coir geotextiles[J]. Geotextiles and Geomembranes, 2008, 26(5):384-392.

[13] Perkins S W. Constitutive modeling of geosynthetics[J].Geotextiles and Geomembranes, 2000, 18(5): 273-292.

[14] 李作攀, 储才元. 非织造布力学性能的模拟及其应用探讨[J].中国纺织大学学报, 1998, 24(2): 1-4.LI Zuo-pan, CHU Cai-yuan. Investigation of mechanical properties simulation and its application for nonwoven fabrics[J].Journal of China Textile University, 1998, 24(2): 1-4.

[15] 林宇亮, 杨果林, 李昀, 等. 加筋土筋材在拉伸荷载作用下的力学特性[J]. 中国铁道科学, 2009, 30(5): 9-14.LIN Yu-liang, YANG Guo-lin, LI Yun, et al. The Mechanical characteristics of the reinforcements under tensile load[J]. China Railway Science, 2009, 30(5): 9-14.

[16] 周蓉, 刘逸新. 土工合成材料拉伸性能模拟及模型分析[J].青岛大学学报: 工程技术版, 2004, 19(2): 47-50.ZHOU Rong, LIU Yi-xin. The analysis of tensile property modeling for geosyntheics[J]. Journal of Qingdao University:Engineering and Technology, 2004, 19(2): 47-50.

[17] Taibi E H. 织物的拉伸应力应变模型[J]. 夏涛, 译. 国外纺织技术, 2002, 205(4): 36-38.Taibi E H. Tensile stress-strain model of fabric[J]. XIA Tao,trans. Textile Technology Abroad, 2002, 205(4): 36-38.