变积分参数模糊PID控制器的设计
2011-06-20马祥兴南京铁道职业技术学院苏州校区
马祥兴 南京铁道职业技术学院苏州校区
在现代温度控制系统中,经常会遇到大惯性、大滞后、非线性的复杂对象,它们都存在许多不确定因素,如采用工业控制中常用的PID控制,很难建立精确的数学模型,难以取得令人满意的控制效果。
近30年来得到迅速发展和受到广泛应用的模糊控制技术,与神经网络、专家控制并称为智能控制技术,在工业控制中特别受到青睐。模糊控制具有鲁棒性强、快速性好、超调量小等优点,对动态特性不易掌握或变化非常显著的复杂系统非常适合。但传统模糊控制由于量化等级有限显得精度不高,且由于量化因子和比例因子是固定的,不能对控制规则进行有效调整,还有它不具有积分环节,很难消除稳态误差,因此,应用范围受到局限。
近一阶段,许多设计者将PID控制与模糊控制结合起来构成模糊PID"双模"复合控制,达到了比较理想的控制效果。它既保留了PID控制无静差、稳态精度高的特点,又保留了模糊控制自适应能力强、动态性能好的特点。
尽管模糊PID控制不失为目前工业控制中一种较好的控制方式,但研究分析和仿真实验表明,该控制方式存在着一些弊端。其主要不足一是引入的积分环节是固定的,使系统存在较大的静态误差;二是量化因子和比例因子是固定的,使系统的动、静态性能难于兼顾。
积分环节的固定,意味着积分参数在控制过程中是一成不变的,系统很难依据控制规则去根据实际工况进行有效调节,降低了系统的自适应能力,使系统存在较大的控制误差。为此,本文提出带有变积分环节的模糊PID控制的方法,即在模糊PID控制的基础上进行改进,引入积分参数可变的控制策略,这不但消除了极限环振荡,还可以完全消除系统静差。
针对量化因子和比例因子固定的不足,本文增加了比例因子可调环节,利用模糊推理产生调节规律,使系统的动、静态性能相得益彰,仿真实验证明控制效果比较理想。
1 变积分参数模糊PID控制原理
1.1 变积分参数模糊PID控制器原理结构
为了实现变积分参数的模糊PID控制方式,对控制器进行改进,其基本原理框图如图1所示。它由模糊PID复合控制器、模糊变积分控制器组成。模糊PID复合控制器由模糊量化、模糊推理、解模糊化和控制规则库A等组成。设控制误差e、误差变化率ec为系统的输入变量,系统的总输出u为输出变量。输入变量经模糊量化后转换成模糊语言变量E、EC,再根据控制规则A进行模糊推理、解模糊化(模糊决策),由控制算法计算出Fuzzy-PID控制器的输出量uf。
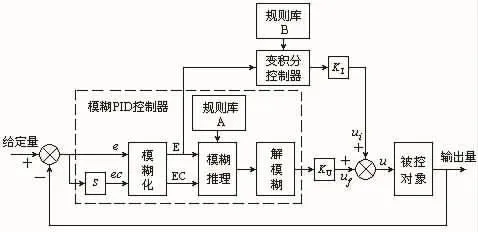
图1 变积分参数Fuzzy-PID控制器的原理框图
模糊变积分控制器实质上也相当于一个模糊控制器,也有与之对应的控制规则库B和控制算法。控制误差e的模糊值E经模糊变积分控制器在线调节后,形成可调的积分参数,以满足不同工况调节的需要。模糊变积分控制器的输出为,则系统总输出的表达式为:

1.2 变积分参数模糊PID控制器的控制方法
常规Fuzzy控制器仅相当于PD控制器,系统的稳态误差较大,为消除系统静差,必须引入积分环节。但引入积分作用的时机要合适,否则会影响系统的控制性能。变积分参数Fuzzy-PID控制器的控制方法采用分段复合控制的方法,分段控制的切换点为:

(2)式中λ为相对给定值的百分比。切换点的控制可采用智能判断的方法,在系统调节初期,控制误差e较大,此时,积分时间常数最大,PID调节作用不突出,可采用模糊控制方式,使系统快速接近期望值。在系统调节后期,系统误差逼近零点时,此时,控制误差e较小,积分时间常数慢慢变小,控制方式将切换为以PID控制为主。由于调节处于误差零值附近,可将系统近似为一个线性系统,只要合理调节PID的参数,尤其是其中的积分参数,就可发挥PID控制在线性系统中的控制优势,实现无差控制。适时引入可变积分环节,采用PID控制+模糊控制的方式,可消除极限环振荡,也可完全消除系统静差,使系统成为无差控制系统。
综观整个调节过程,变积分参数的模糊PID控制原理是:根据不同阶段对控制参数的要求,结合系统各阶段的控制误差e和误差变化率ec的状况,采用分段控制的方法,以满足系统对控制的要求。在调节后期,突出变积分控制的功能,控制中自动在线调整积分参数,以增强实时控制性能,提高稳态精度和自适应能力。因此,它是一种高精度高性能的"双模"结构的模糊PID控制器,系统的鲁棒性强,控制精度高,大大提高了系统的控制品质。
2 变积分参数模糊PID控制器的设计
2.1 确定输入、输出变量的论域和模糊子集
根据一般温控系统的工作特点,结合铝箔退火炉温度控制的操作经验,确定e、ec、uf和ui的基本论域分别为(-3,3)、(-0.3,0.3)、(-5,5) 和(-0.6,0.6),则它们对应的论域和模糊子集为:
将E、EC量化为15个等级,离散化的论域 E、EC={-6,-5,-4,-3,-2,-1,-0,0,+0,+1,+2,+3,+4,+5,+6};
将Uf分为13个等级,离散化的Uf={-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6};
将Ui分为4个等级,离散化的Ui={0,0.02,0.04,0.06}。
将E、EC的模糊子集分为9档,能完全满足高性能控制的要求,即{NB,NM,NS,NZ,Z,PZ,PS,PM,PB};
Uf的模糊子集分为 8 档:{NB,NM,NS,NZ,PZ,PS,PM,PB};
Ui的模糊子集分为 4 档:{Z,PS,PM,PB}。
考虑到对论域的覆盖程度、鲁棒性和稳定性,选择分辨率较高的三角形隶属函数为各模糊子集的隶属函数。
2.2 确定模糊控制规则
为减少控制规则数,分设两个规则库,规则库A用于模糊PID控制,规则库B用于模糊变积分参数控制。模糊PID控制高于变积分参数控制,所以uf的模糊子集较多,规则库A中的规则也多些。
2.2.1 确定规则库A
设计时先确定PID参数与误差e和误差变化率ec间的模糊关系,以便确定模糊控制算法。控制过程中则不断检测误差e和误差变化率ec的即时数值,按控制规则对PID参数进行在线自动调整。模糊PID控制器的控制规则常采用下列语句:
If e is A and ec is B then u is C
设计规则库A时应考虑系统的误差值尽可能地小,并充分考虑PID3个参数kP、ki和kd对系统性能的影响,按各自的影响程度在不同的e和ec以及在不同的调节阶段作出不同的调节策略,形成一系列的模糊规则。模糊PID控制器的规则表如表1所示。
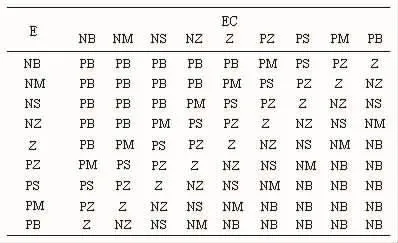
表1 Fuzzy-PID控制器规则表
2.2.2 确定规则库B
设计规则库B时应考虑系统的静差和超调量要尽量地小,设计的关键是能满足不同阶段对积分参数的要求。在系统调节初期,以规则库A为前件控制,此时误差e较大,ki为零,控制方式主要为模糊控制,利于系统有较强的鲁棒性和较好的快速性。在系统调节后期,误差e接近零点,此时误差e较小,ki将逐步增加,将控制切换为PID控制+模糊控制,这时两个规则库A与B重叠控制,实现模糊变积分参数下的模糊PID控制。在切换过程中,由于积分参数连续可调,避免了切换时产生的"毛刺"。变积分环节的控制规则表如表2所示,表中"×"为积分控制死区,它由模糊控制实现。该表采用不对称结构,是为了在系统出现超调时能迅速抑制。
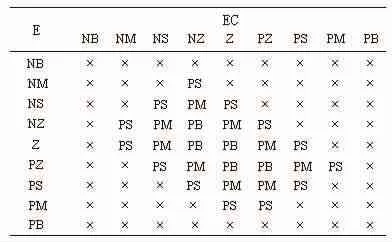
表2 变积分环节控制规则表
由于输出采用两路叠加的方法,因此,必须把所有规则对应的输出值,根据实际应用的需要进行统整,使所有控制规则有机融为一体。
2.3 模糊推理及比例因子调节的设计
设计中一般用控制规则来表达控制策略,再用模糊推理及控制算法,计算出模糊控制表,实时控制时采用在线查询控制表的方式来确定输出控制量化值,最后,计算机将此量化值乘以调节因子α,得到实际输出的控制量。控制表一般事先通过离线计算的方法来确定。
常规模糊控制器输出比例因子kU的值会直接影响系统性能,如要系统快速性好则应加大kU值,如要系统稳态精度高则应减少kU值,为解决这一矛盾,可在变积分环节中增加相应的比例因子kI。在仿真中,通过整定kU来保证快速响应,通过调节kI来保证稳态精度。参数的优化可通过仿真来确定,以避免盲目性。在整个输出响应过程中,设定α(t)为一个调整因子,调节规律由模糊推理过程产生。根据当前的控制误差e、误差变化率ec,结合动态响应和控制经验,产生一个模糊变量H,经解模糊化得到新的调整因子,即:

(3)式中 η 为α(t)的调整率。将kU乘以调整因子得到实时控制下的kU(t)的调节规律:

根据(4)式的调节规律,可在线调节kU(t)的动态参数。
按类似方法,kI也可设一个调整因子α1(t),专门用于积分作用的调节,以满足积分输出有一个合适的控制量,kI(t)的调节规律为:

这样,用kI(t)就可调节积分环节的输出控制量,间接调整了控制规则。kU(t)和kI(t)两者有机配合,可使系统的动、静态性能互相兼顾,大大提高了控制效果。
3 系统仿真研究
仿真的目的是根据上述设计的控制方案,利用Matlab语言,通过跳跃逃逸控制算法,求得优化的积分参数ki、比例因子kU(t)和kI(t),以增强系统的控制效果。
3.1 仿真模型和仿真过程
选择代表典型的二阶系统铝箔退火炉温控系统作仿真对象,系统的传递函数为:

利用Matlab的simulink和Fuzzy logic toolbox工具箱对变积分参数模糊PID控制系统进行仿真,图2是它的仿真模型。仿真过程分为两步:一是对积分参数ki、比例因子kU(t)和kI(t)、调整因子α(t)进行仿真,仿真中不断优化参数的取值,二是对系统响应进行仿真,重点考察系统响应特性,如响应速度、调节时间、超调量和稳态误差。

图2 变积分参数Fuzzy-PID控制仿真模型
3.2 仿真结果与比较
根据定义和操作经验,kU和kI的初始值由下式给定:

选取调整因子的初始值为α=0.5、α1=0.4,选取 PID 参数kP=7.6、ki=0.02、kd=32。经过优化仿真后得到:ki=0.015~0.035,kU=2.4、kI=0.6,α(t)=0.35~0.65,α1(t)=0.15~0.45。仿真中得到的系统动态响应曲线如图3所示,曲线1是采用常规PID控制的响应曲线,曲线2是采用变积分参数模糊PID控制的响应曲线,通过比较可以看到,变积分参数模糊PID控制的超调量、稳态误差和动态响应速度都有了明显的改善,控制性能大大优于常规PID控制。
仿真实验不但优化了相关的控制参数值,为系统的开发应用提供了宝贵的数据;同时也完善了控制方案,奠定了方案的可行性,为现场设备升级积累了实际经验,产生较好的指导作用。
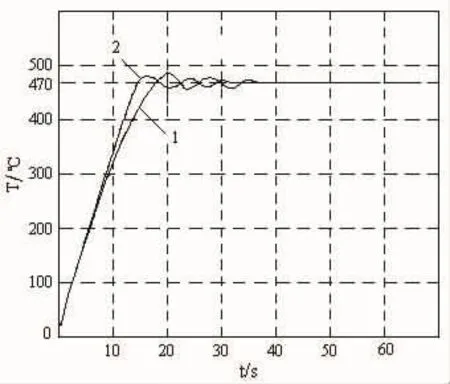
图3 系统输出响应曲线
4 结束语
本文提出的变积分参数的模糊PID控制方案,它以模糊控制为前件,模糊变积分参数控制为后件,以模糊控制为粗调,变积分参数控制为细调。采用分段控制的方法,在模糊控制的基础上切换到PID控制,以满足不同工况对调节的要求,最终使控制误差逐步向零点逼近,实现无差控制。在系统结构上,增设了模糊变积分环节和控制规则库B,通过模糊推理对积分参数进行实时在线调节,增强了系统的鲁棒性和自适应能力。同时,在设计中增加了可调节的比例因子,兼顾了系统的动、静态性能,大大提高了控制效果。
本文以现场的设备升级为背景,可行性强,系统开发快、成本低、可靠性强,智能化程度高,控制品质好,可推广到其它大滞后、大惯性、非线性的复杂温控场合。
