HMX/TNT炸药爆速与曲率及组分关系实验研究*

张宏亮，Shakeel A R，黄风雷

(北京理工大学爆炸科学与技术国家重点实验室，北京 100081)

爆轰波传播问题是爆轰物理研究的重要问题之一，目前带反应区的爆轰波传播理论问题仍没有完全解决。20世纪80年代，在Whitham冲击动力学基础上，J.B.Bdzil等［1］提出了爆轰冲击波动力学方法，即DSD方法。该方法使多维爆轰波传播研究走向实用阶段，可解决一些工程设计问题。DSD方法被认为是目前研究爆轰波非理想传播的可行途径，该方法证明爆轰波法向速度Dn与当地曲率κ密切相关。目前Dn(κ)关系难以从理论上导出，一般通过曲面爆轰波传播实验标定。在J.B.Bdzil之后，针对DSD实验参数标定做了大量工作［2-4］，这些工作主要集中在PBX-9501、PBX-9502和EDC-35炸药。孙承纬［5］、谭多望等［6］、赵继波等［7］针对JB-9014炸药标定了大量DSD实验参数，并相应开展了一系列有关DSD方法的研究;A.R.Shakeel等［8］针对 RDX/TNT炸药开展了 DSD方法的实验研究。目前针对HMX/TNT炸药的DSD方法研究工作还不多，本文中，采用光电联合测试方法测量常温下质量配比分别为60/40、50/50和40/60时HMX/TNT炸药的定态爆速和波形，根据拟合的爆轰波形标定DSD实验参数，并进一步分析不同炸药配比对法向速度Dn与当地曲率κ关系的影响。

1 实验方法

爆轰装置如图1所示，用雷管起爆主装药(HMX/TNT注装炸药)药柱，主装药药柱长度必须足够长以保证在测速段之前形成拟定态爆轰波。实验装置布局如图2所示，爆速由2组对称布置的电探针测量，拟定态爆轰波形通过转镜式高速摄影相机测得，相机扫描速度为1 r/ms，即 3.003 km/s。

图1 爆轰装置示意图Fig.1 Rate stick design

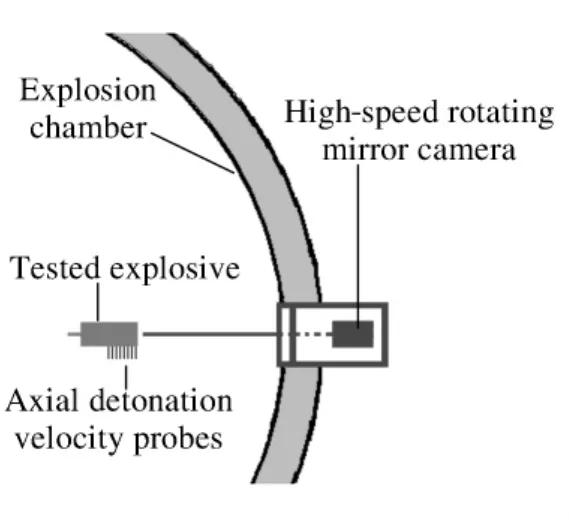
图2 实验装置布局图Fig.2 Experimental layout

2 实验结果及分析

2.1 定态爆速及定态波形

定态爆速及药柱参数列于表1。典型的波形测量结果如图3所示，底片中定态爆轰波形前沿和边界都很清晰，说明采用高速扫描相机直接从爆轰装置端部狭缝中测爆轰波形的方法是可行的。读取底片波形数据的方法如下:先根据相机的扫描速度计算爆轰波到达药柱端面的时间，将该时间乘以定态爆速D0得到波阵面曲线波形。

常见的波阵面曲线拟合形式ln(cos(r))级数、ln(J0(r))级数(J0为零阶Bessel函数)和Chebyshev多项式。本文中采用ln(cos(r))级数对DSD实验参数进行拟合，具体表达式为

式中:z(r)是波阵面曲线，r是波阵面上的截面圆半径，R是药柱半径，an和b是拟合参数。拟合参数列于表2，拟合结果如图4所示。

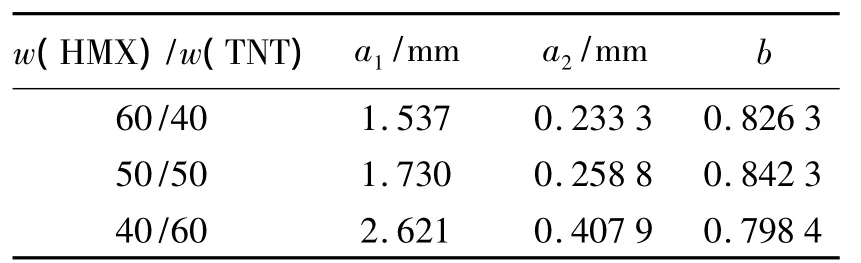
表2 波阵面曲线拟合参数Table 2 Fitting parameters of wave front

图3 典型的爆轰波形数字底片Fig.3 Typical film record of detonation

图4 波阵面z-r曲线Fig.4 Wave front data of z-r

2.2 D n(κ)曲线

Dn(κ)由定态爆速D0和波阵面曲线z(r)计算。由几何关系可得法向爆速表达式为

表3 D n(κ)关系拟合参数Table 3 Fitting parameters of D n(κ)

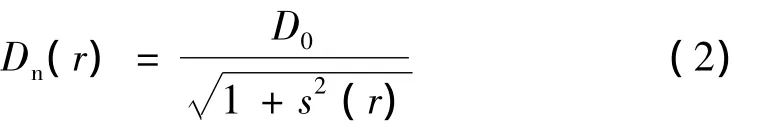
波阵面上当地平均曲率κ表达式为

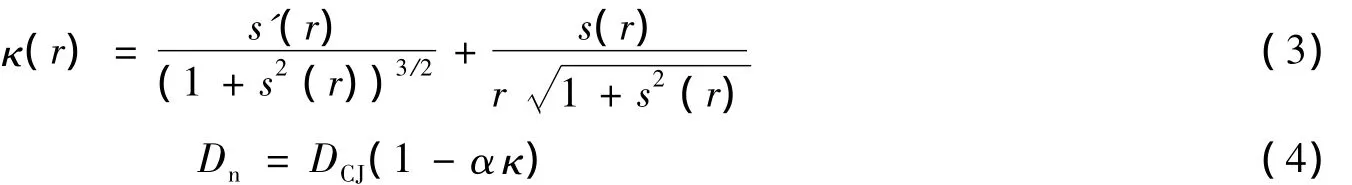
式中:s(r)=dz/dr。联立式(2)～(3)可得Dn(κ)关系，然后根据式(4)标定DSD实验参数，其中DCJ和α是需要实验标定的参数，拟合参数列于表3。根据拟合结果给出Dn(κ)关系如图5所示，TNT含量从40%变化到60%，Dn(κ)曲线的斜率逐渐增大，且斜率增大的速率为正值。

图5 D n(κ)关系图Fig.5 Relation curves of D n(κ)

3 广义D n(κ)关系

利用DSD方法研究炸药的非理想爆轰行为需要确定Dn(κ)的定量关系，即标定DSD实验参数。为了减少实验标定费用，通过分析实验数据对不同配比条件下的Dn(κ)关系进行了研究。

由图4分析知，HMX/TNT注装炸药随着TNT含量增加，爆轰波延滞距离z增大，即满足

随着炸药密度ρ增大，爆轰波延滞距离z减小，即满足

炸药中TNT含量w(TNT)和炸药密度ρ是影响DSD实验标定参数的主要因子，现引入新变量

通过变量Rt将实验标定的Dn(κ)关系推广为广义Dn(κ)关系，即Dn(κ，Rt)关系。Dn(κ，Rt)关系是将需要实验标定的参数DCJ和α通过含有Rt的函数求出，即根据式(8)和式(9)求得参数DCJ和α，式(8)和式(9)是根据已有实验参数归纳拟合出的关系式。将式(8)和式(9)代入式(4)可得Dn(κ，Rt)关系，如式(10)所示。任意给定变量Rt就可以通过Dn(κ，Rt)关系得出相应未标定的Dn(κ)关系，进而减小实验标定费用。

已有实验数据:w1(TNT)=40%，ρ1=1.744 g/cm3，Rt1=22.936 cm3/g;w2(TNT)=50%，ρ2=1.716 g/cm3，Rt2=29.138 cm3/g;w3(TNT)=60%，ρ3=1.685 g/cm3，Rt3=35.608 cm3/g。因此，该Dn(κ，Rt)关系最佳预测范围为 22.936 cm3/g≤Rt≤35.608 cm3/g。

式中:ci和di是通过表 3 中实验参数拟合求得的:c0=8.003 61，c1=0.033 01，c2= －0.001 13;d0=4.482 35，d1= －0.289，d2=0.005 95。

图6 D n(κ，R t)关系图Fig.6 Relation curves of D n(κ，R t)

图7 R t-z-r关系图Fig.7 Relation curves of R t-z-r

根据Dn(κ，Rt)关系编写了相应程序，通过该程序可以在给定Rt的情况下，给出相应的Dn(κ)关系，根据该程序给出的Dn(κ，Rt)关系如图6所示;该程序根据Dn(κ，Rt)关系可进一步求出相应的z-r关系，并给出Rt-z-r关系如图7所示。

为验证Dn(κ，Rt)关系的可信性，将通过Dn(κ，Rt)关系预估的z-r关系与文献［9］中给出的z-r关系作对比，如图8所示。从图中可以看出，Dn(κ，Rt)关系预估结果与实验结果［9］吻合较好。该对比结果是在w(TNT)=1，ρ=1.62 g/cm3，Rt=61.728 cm3/g 的条件下得出的，而在 22.936 cm3/g≤Rt≤35.608 cm3/g范围内Dn(κ，Rt)关系预测精度应高于Rt=61.728 cm3/g的精度，故该Dn(κ，Rt)关系的预测效果是可信的。

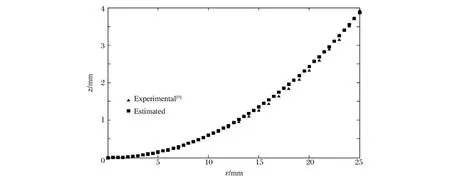
图8 w(TNT)=1的条件下预估的z-r关系与实验结果的比较Fig.8 Comparison of estimated z-r curve with experimental result［9］ at w(TNT)=1

4结论

研究了不同配比条件下HMX/TNT注装炸药的Dn(κ)关系，爆轰波延滞距离z随TNT的含量增加而增大;爆轰波延滞距离z随着炸药密度ρ增大而减小;随着TNT含量增加Dn(κ)曲线的斜率逐渐增大，且斜率增大的速率为正值。还将Dn(κ)关系推广为Dn(κ，Rt)关系，在22.936 cm3/g≤Rt≤35.608 cm3/g范围内，任意给定Rt，可给出相应的Dn(κ)关系，并可进一步给出Rt-z-r关系，该方法可以减少实验标定次数，且有一定的准确度。

［1］Bdzil JB，FickettW，Stewart D S.Detonation shock dynamics:A new approach tomodelingmulti-dimensional detonation waves［C］∥Proceedings of the 9th International Symposium on Detonation.Portland:Office of Naval Research，1989:730-742.

［2］Bdzil JB，DavisW C.Detonation shock dynamics(DSD)calibration for PBX9502［C］∥Proceedings of the 10th International Symposium on Detonation.Boston:Office of Naval Research，1993:146-149.

［3］Hill L G，Bdzil JB，Aslam T D.Front curvature rate stick measurements and detonation shock dynamics calibration for PBX 9502 over a wide temperature range［C］∥Proceedings of the 11th International Symposium on Detonation.Colorado:Office of Naval Research，1997:1029-1037.

［4］Aslam TD，Bdzil JB，Hill LG.Extensions to DSD theory:Analysis of PBX 9502 rate stick data［C］∥Proceedings of the 11th International Symposium on Detonation.Colorado:Office of Naval Research，1997:21-29.

［5］孙承纬.爆轰传播理论的解析研究方法:六［J］.爆炸与冲击，1992，12(1):89-96.

SUN Cheng-wei.Analytic methods in the theory of detonation propagation:Ⅵ［J］.Explosion and Shock Waves，1992，12(1):89-86.

［6］谭多望，方青，张光升，等.钝感炸药直径效应实验研究［J］.爆炸与冲击，2003，23(4):300-304.

TAN Duo-wang，FANG Qing，ZHANG Guang-sheng，et al.Experimental study of the diameter effect for JB-9014 rate sticks［J］.Explosion and Shock Waves，2003，23(4):300-304.

［7］赵继波，谭多望，赵锋，等.带壳钝感炸药非理想爆轰实验研究［J］.含能材料，2005，13(4):217-221.

ZHAO Ji-bo，TAN Duo-wang，ZHAO Feng，et al.Experimental study on the non-ideal detonation of IHE with confinements［J］.Energetic Materials，2005，13(4):217-221.

［8］Shakeel A R，HUANG Feng-lei.Detonation shock dynamics relations for RDX-TNT based cast explosives［J］.Journal of Beijing Institute of Technology，2007，17(2):138-142.

［9］Sandstrom FW，Abernathy R L，Leone M G，et al.Diameter effectand detonation front curvature of ideal and non-ideal explosives［C］∥Shock Compression of Condensed Matter-1999，2000，505(1):826-828.