基于过程法构建二维数字岩心

盛金昌,何光宇,周治荣,姚德生,詹美礼,罗玉龙

(1.河海大学水利水电学院,江苏南京 210098;2.中国水电顾问集团成都勘测设计研究院,四川成都 610072;3.广西电力工业勘察设计研究院,广西南宁 530023;4.中水北方勘测设计研究有限责任公司,天津 300222)

达西定律是研究多孔介质渗流的基础,它是建立在宏观试验的基础上,无法对细观孔隙尺度的渗流进行描述,而石油开采等领域迫切需要从细观孔隙角度出发研究渗流问题.目前多孔介质渗流的一些细观机理可以通过物理试验来定性研究,但缺少科学的理论和技术来进行定量描述.目前国内外已有不少学者开展了这方面的研究,而构建细观孔隙网络模型,即数字岩心是其中一项基础性的工作.

自1956年Fatt[1]首次引入真正意义的孔隙网络模型以来,随着计算机和图像分析技术的发展,很多学者[2-6]对孔隙网络模型进行了研究.构建数字岩心有3类方法,即切片组合法、基于切片分析的图像重建法和X射线立体成像法.基于切片分析的图像重建法是基于二维岩心切片扫描图像的构建方法,只需少量的岩心切片,而岩心切片在石油开采中常被用来进行地质评价,较易获得,故该方法被大多研究所采纳.研究[7-8]表明,将传统的两点相关函数(随机法)用来描述多孔介质结构,尤其是孔隙之间的连通关系是不够充分的.本文在前人研究的基础上,基于过程法编程实现了二维数字岩心的构建,并对结果进行了可视化处理.

1 过程法构建数字岩心原理

过程法是Bakke等[4]于1997年提出的,它是在对二维岩心切片分析的基础上,结合岩心的颗粒粒径分布特性,通过对沉积类岩石3个形成过程(沉积、压实和成岩)的模拟来构建数字岩心的.文献[8]指出:建立准确、可靠的数字岩心所需的输入数据可以从标准的岩石切片中获得,这些输入数据包括粒度分布、孔隙度、压实程度的视觉估计、黏土材料、胶结物的类型和数量等.

1.1 模拟沉积过程的算法

基于过程法构建数字岩心的沉积模拟主要采用颗粒随机堆积模型(分为连续堆积法和重整化群法2种方法)[9],本文采用连续堆积法.

1.1.1 基本假设

岩石颗粒沉积过程十分复杂,为简化算法,在不影响沉积规律的前提下,进行如下假设[4,10-11]:(a)所有颗粒均为球体;(b)颗粒初始下落位置是随机的,且各点几率均等;(c)考虑沉积结构的稳定性,忽略由于重力压实引起的颗粒形变和结构重组效应;(d)颗粒下落时沿着重力势能梯度下降最大的方向运动;(e)颗粒在下降过程中只受重力作用,忽略侧向作用力;(f)颗粒下落达到相对平衡位置以后,其位置保持不变;(g)下降颗粒与已沉积稳定颗粒发生碰撞时不发生弹跳;(h)在下落颗粒达到平衡位置以后,下一颗粒才开始下落;(i)二维模拟时沉积区域为一矩形区域.

1.1.2 沉积过程模拟

沉积过程模拟得到的是岩心颗粒的松散堆积体.模拟步骤为:(a)随机生成第1层,作为表层颗粒链.(b)在粒度分布曲线上随机抽取1个颗粒,半径为Rd,在沉积区域(0≤x≤Lxmax,y≥0),根据式

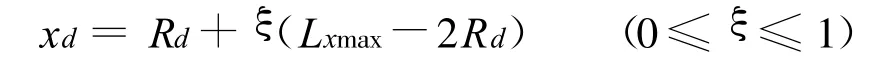
随机生成下落颗粒的x坐标(ξ为随机产生的数),其y坐标取为常数y0.(c)根据xd与表层颗粒链中颗粒的x坐标之间的关系,确定与下落颗粒碰撞的表层链颗粒.(d)计算下落颗粒中心坐标,判断其稳定性,如果不稳定,向左或者向右滚动1个颗粒,重复第(c)步,反复操作,直到颗粒达到稳定位置.二维情况下颗粒最终平衡位置有4种,如图1所示.(e)记录下落颗粒的中心坐标及其半径.(f)根据下落颗粒的中心位置与目前表层链颗粒中心位置的关系,更新表层颗粒链.(g)判断所需颗粒数是否已沉降完毕,如果是,则结束沉积模拟,反之继续第(b)～(g)步,直到所有颗粒沉降完成.

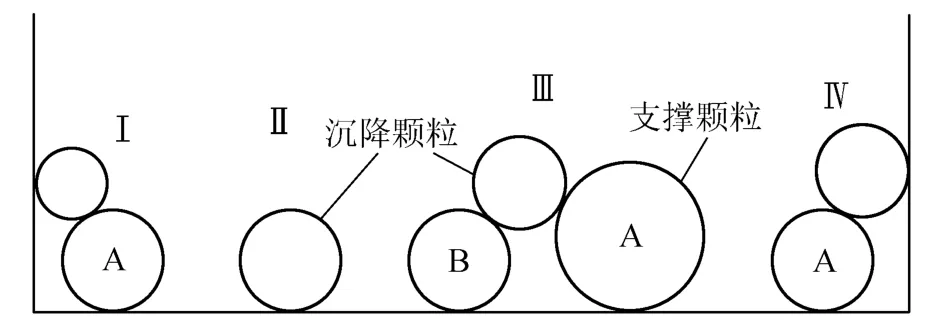
图1 颗粒二维堆积过程中的4种可能平衡位置Fig.1 Four possible equilibrium positions of 2D particle accumu lation

1.2 模拟压实过程的算法

岩石的压实过程是指受到来自上层岩石的重力以及周围岩石、流体的接触压力和摩擦力等作用后,岩石颗粒发生平动或转动2种运动,是一个非常复杂的过程.文献[4,7]认为,下覆岩层受到上覆岩层压实后,其总体积和孔隙度下降,因此在算法实现时,应引进一个压实因子来描述孔隙减少程度;Jin等[10]则从动力过程来考虑岩石的压实过程.本文进行了如下假设:颗粒的几何形状不发生变化,无侧向位移,颗粒不发生转动,颗粒无弹性变形,只通过改变各个颗粒的垂直坐标来实现岩石的压实过程.对于不同的岩石压实程度,通过引入压实因子 λ,使构建的数字岩心与真实岩心相符合.λ的取值范围是[0,1],λ越大表示岩石受压缩程度越大,反之则越小.

二维空间压实前后颗粒相对位置的关系为

式中:y——压实后的坐标;y0——压实前的坐标.

1.3 模拟成岩过程的算法

成岩过程是指未固结的疏松沉积物变为坚硬岩石的过程.这一过程十分复杂,包含了物理、化学、力学和生物化学等各种作用,这些作用从沉积到变质一直影响着沉积物的各种特性.本文对成岩过程中的主要部分——矿物质的胶结作用进行研究.胶结作用是矿物质沿岩石颗粒表面结晶和沉淀的过程,最普通的矿物质胶结类型是石英胶结物.

Roberts等[12]首次提出了一致增长颗粒固结模型.为了提高该模型的适用性,Schwartz等[13]提出了一个模拟颗粒胶结作用的交替增长算法:

交替增长算法认为增长速率应该依赖于增长方向.对于每一个增长方向r,定义 Δ为初始球(R)表面与Wigner-Seitz方块边界之间的距离,通过引入增生指数β来控制颗粒中心与孔隙和颗粒界面之间距离的增长速率,参数 α用于控制增长数量.

Jin等[10]提出了一种改进的颗粒生长算法,该算法与文献[12-13]的算法不同,考虑了硅石胶结增生率和岩石颗粒大小对岩石颗粒增长的影响:

式中:Δ(r)——矿物质胶结增生从岩石颗粒中心沿r方向的增量;¯R——所有颗粒的平均半径;R0——原始颗粒的半径;l(r)——沿r方向原球形颗粒表面到该颗粒对应的多边形表面或者与其相邻颗粒表面之间的距离;L(r)——从颗粒中心到孔隙胶结表面的距离;κ——参数,控制孔隙度下降数量.

根据文献[12-13]的原理,笔者编制程序模拟了岩石的成岩过程.图2给出了α分别为-2,0和2时岩石颗粒石英胶结增生图(图中原岩石颗粒为白色,石英胶结物为灰色,孔隙空间为黑色).对比图2可以看出:(a)若α＜0,胶结物优先在大颗粒的表面生长,多数的胶结物沉淀在大颗粒的表面;(b)若 α=0,胶结物均匀地沉淀于所有岩石颗粒的表面;(c)若α＞0,胶结物优先在小颗粒表面生长,多数的胶结物沉淀在小颗粒的表面.从物理观点分析来看,参数α取正值似乎更合理并与现实相符,因为小颗粒比大颗粒具有更大的比表面积.

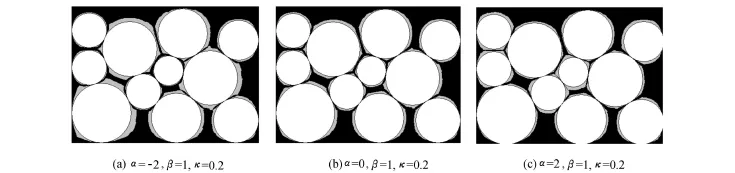
图2 不同α条件下岩石颗粒的石英胶结Fig.2 Quartz cementation around rock particles under different values of α

图3为β不同时岩石颗粒石英胶结增生图.β可以取任意数(负数、零或正数),本文β分别取-1,0,1来代表负数、零或正数对岩石颗粒石英胶结增生的影响.从图3可以看出:(a)若 β＜0,石英胶结物优先在喉道中生长,优先沉淀在狭窄的岩石颗粒接触区域,降低了孔隙的面容比.当孔隙空间变得不连贯时,这种生长倾向于保持大孔隙的连贯性.(b)若β=0,石英胶结物在孔隙和喉道中均匀生长,均匀地沉淀于所有颗粒表面.(c)若β＞0,胶结物优先在孔隙中生长,多数胶结物沿着 l(r)最大方向沉淀.这种类型的胶结倾向于增加原孔隙空间的孔隙面容比,并且当孔隙度非常低时,会使孔隙空间相互连接.总之,β影响着胶结增生的几何趋势.

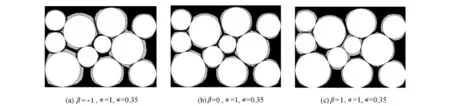
图3 不同β时岩石颗粒的石英胶结Fig.3 Quartz cementation around rock particles under different values of β

2 构建二维数字岩心实例及可视化

2.1 颗粒半径分布曲线

应用计算机图像处理技术对高分辨率的二维岩心薄切片图像进行分析处理,可得试验样本建模所需参数.假设所有的颗粒都是圆(球)形颗粒,通过光散射原理计算可构造出粒度分布曲线.本文选取240个岩石颗粒,假设最小岩石颗粒的半径为10μ m,最大岩石颗粒半径为600μ m,经过处理,得到如图4所示的一条岩石颗粒半径及其编号分布曲线.

2.2 沉积模拟

根据颗粒随机堆积过程基本思想,笔者采用MATLAB软件编制了岩石颗粒在二维空间中随机沉积模拟程序,并用MATLAB软件实现了随机沉积结果的可视化.在图4所示的曲线上选取81个颗粒进行1次沉积模拟(每个编号对应1个颗粒半径),可视化结果如图5所示.因为随机模拟,每次模拟都会呈现不同的结果.

2.3 压实模拟结果

将沉积模拟结果作为初始输入数据进行压实算法模拟,得到的岩石压实模拟结果如图6所示,其中λ分别为0.05,0.1,0.20,随着λ的增大,孔隙不断缩小.

图4 岩心颗粒粒度与编号分布关系Fig.4 Relationship between rock particle size and particle number

图5 二维沉积模拟结果(白色为岩石颗粒)Fig.5 Results of 2D deposition simu lation(where white denotes rock particles)

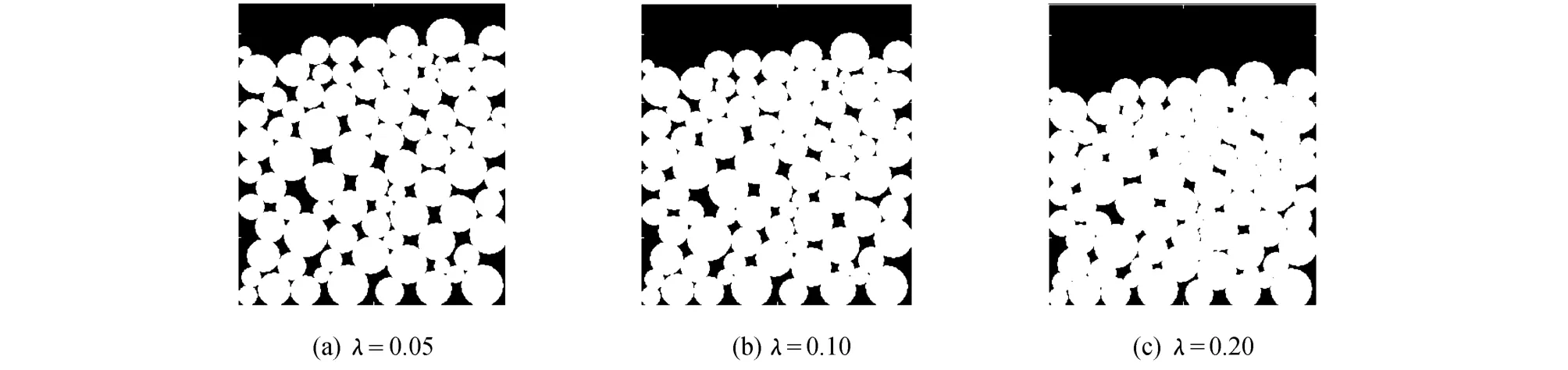
图6 二维压实模拟不同λ的压实对比(白色为岩石颗粒)Fig.6 Results of 2D compaction simu lation with different values of λ(where white denotes rock particles)

2.4 成岩模拟结果

成岩模拟采用改进的交替增长算法,在压实模拟数据的基础上进行,在此取 λ=0,α=1,β=1,κ=0.2来模拟岩心颗粒石英胶结增生,结果如图7所示.

图7 岩石颗粒的石英胶结增生结果Fig.7 Overgrow th results of quartz cementation

3 结 语

岩石类多孔介质的渗流特性非常复杂,以往的研究多集中于宏观意义上的渗流问题.目前,尽管可以通过实验来研究多孔介质中细观渗流的一些机理,但还缺少必要的手段和科学合理的方法对细观渗流进行定量描述.在孔隙级别上研究多孔介质细观渗流问题,建立一套可以准确描述细观渗流机理的理论体系,具有非常重要的理论意义和应用价值,而数字岩心则是开展细观渗流机理研究的基础.

本文在前人工作的基础上,基于过程法编程完成了二维数字岩心的构建工作,并实现了二维岩心的可视化.在岩心构建过程中,参数α控制着石英胶结物沉淀的优先位置,增生指数 β控制着石英胶结物优先增生的几何趋势,κ则控制着孔隙度下降的数量,压实因子λ反映上覆岩层压力,压实因子越大,孔隙压缩程度越高.

[1]FATT I.The network model of porous media:I capillary pressure characteristics[J].Transactions of AIME,1956,207(1):144-159.

[2]JOSH I M.A class of stochastic models for porous media[D].Law rence Kansas:University of Kansas,1974.

[3]HAZLETT R D.Statistical characterization and stochastic modeling of pore networks in relation to fluid flow[J].Mathematical Geology,1997,29(6):801-822.

[4]BAKKE S,ØREN P E.3-D pore-scale modeling of sandstones and flow simulations in the pore networks[J].SPE Journal,1997,2:136-149.

[5]STREBELLE S.Sequential simulation drawing structures from training images[D].Palo Alto:Stanford University,2000.

[6]OKABE H,BLUNT M J.Prediction of permeability for porous media reconstructed using multip le-point statistics[J].Physical Review E,2004,70:106-135.

[7]BISWAL B,MANSWARTH C,H ILFER R,et al.Quantitative analysis of experimental and synthetic microstructures for sedimentary rocks[J].Physics A,1999,273:452-475.

[8]ØREN P E,BAKKE S.Process based reconstruction of sandstones and predictions of transport properties[J].Transport in Porous Media,2002,46(2):311-343.

[9]HE D,EKERE N N.Computer simulation of powder compaction of spherical particles[J].Journal of MaterialsScience Litters,1998,17:1723-1725.

[10]JIN G,PATZEK T W,SILIN D Y B.Physics-based reconstruction of sedimentary rocks[R].Richardson:SPE,2003:305-318.

[11]薄启炜,董长银,张琪,等.砾石充填层孔喉结构可视化模拟[J].石油勘探与开发,2003,30(4):108-110.(BO Qi-wei,DONG Chang-yin,ZHANG Qi,et al.Pore filling gravel layer structure visualization simu lation[J].Petroleum Exploration and Development,2003,30(4):108-110.(in Chinese))

[12]ROBERTS J N,SCHWARTZ L M.Grain consolidation and electrical conductivity in porous media[J].Physical Rev B,1985,31(9):5990-5997.

[13]SCHWAR TZ L M,KIMMINAU S.Analysis of electrical conduction in the grain consolidation model[J].Geophysics,1987,52(10):1402-1411.