ALE法在扩底桩上拔承载力有限元分析中的应用

陈 榕，郝冬雪，樊广森

(1.东北电力大学建筑工程学院，吉林吉林132012;2.大连理工大学岩土工程研究所，辽宁大连116085)

扩底桩因具有单桩承载力高，抗拔承载力强等优点而在地基土质较好的地区得到广泛的应用。国内很多学者对均质地基中大直径扩底桩单桩的承载变形机理及承载性状开展了研究工作［1-5］。上述研究中普遍采用了模型试验和有限元数值模拟两种方法。与模型试验相比，数值模拟方法具有耗时短、成本低及可重复性等诸多优点，并且随着计算机技术的高速发展和计算方法的不断创新，有限元数值模拟方法所占比重逐渐增大。但在有限元计算中由于土体网格变形过大，往往产生严重的畸变问题，导致有限元计算的收敛性较差。因此，在本文分析中拟采用ALE法解决填土中由于大变形所导致的网格畸变问题，同时对不同桩径比的扩底桩的承载力变化也进行了简单的初步分析。

1 ALE法介绍

ALE(Arbitrary Lagrangian Eulerian)方法，即任意拉格朗日-欧拉法，结合了传统的拉格朗日方法和流体分析常采用的欧拉方法的优点。该方法具有以下两个优点:

(1)ALE法在空间差分上，采用中心差分和上风差分相结合的混合差分法，并且采用显、隐式结合的方案，在周向上采用隐式差分，其它方向采用显式差分，差分单元可以是任意四边形或任意六面体，速度定义在单元角点上，而其它参数(如压力、密度、温度、能量等)定义在单元的几何中心，因而动量方程和其它因变量方程的网格系统是相互交错的。

(2)ALE的差分网格具有可按规定速度运动的灵活性。拉格朗日方法把坐标随流体运动，对流项为零;而欧拉方法把坐标在空间固定，对流项由流体运动决定。ALE方法使用的坐标运动方式可以自由的定义，对流项由流体运动和坐标运动决定。ALE方法中，如果坐标速度取为流体速度退化为拉氏方法，取为0则退化为欧拉方法。即网格按当地流体速度运动时，计算是拉格朗日方式;当网格固定不动时，计算则是欧拉方式。

2 扩底桩有限元模型

本文通过大型商业有限元软件ABAQUS，采用ALE方法对扩底桩的上拔特性进行了有限元分析。由于算例中的荷载和边界均为轴对称结构，因此模型中采用轴对称单元建模，见图1。

图1为均质地基中在竖向上拔荷载作用下扩底桩的轴对称模型。扩底桩上径为0.6 m，底径为1.2 m，桩身长度为3.4 m。模型的宽度为扩底桩上径的5倍，深度为扩底桩长度的3倍，采用位移加载。左侧空白部分为扩底桩，与填土相比，桩体的刚度较大，因此在分析中将桩体假设为解析刚体构件。右侧部分为均匀粉土，土体为Drucker-Prager理想弹塑性模型，采用非关联流动法则，相关计算参数见表1。

有限元模型中采用面-面(Surface to Surface)接触法则对扩底桩与土体之间的接触行为进行定义，扩底桩外侧为“主动面”，土体为“被动面”。同时，将两者之间的法向接触特性定义为“硬性接触”，界面间不产生截面渗透;对于土体和扩底桩之间的切向接触特性，采用“罚函数”摩擦公式。主动面与被动面之间的摩擦系数可通过土工界面试验获得。在法向的接触特性上，接触状态由接触面上的法向压强决定。当两个接触面处于接触状态时，法向压力为正，压力通过接触面可以传递。当法向应力减小至零或负的时候，接触面开始分离;而分离的接触面重新接触的时候，意味着法向压力重新为正。

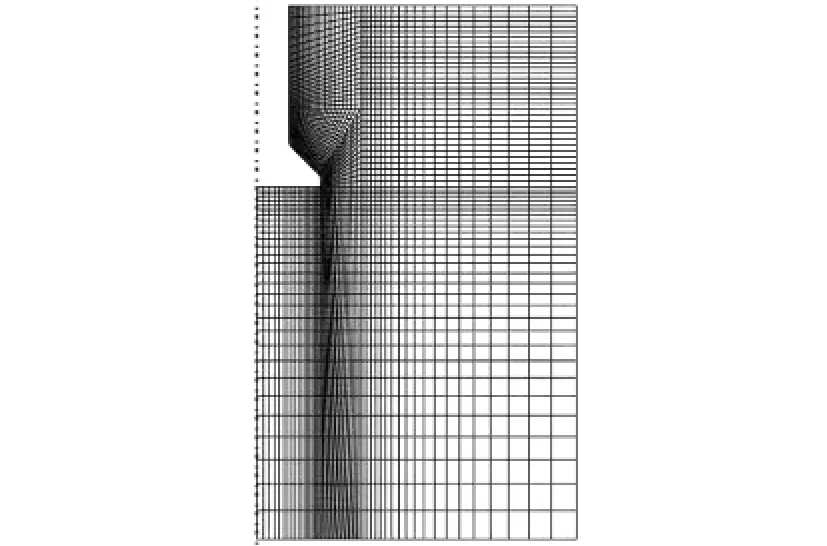
图1 轴对称模型初始网格结构

表1 地基土计算参数

3 结果分析

图2为上拔荷载与位移的关系曲线，当上拔位移

-荷载曲线逐渐接近水平时，表示在上拔荷载不变时，上拔位移仍持续增长，认为桩周围土体达到了极限平衡状态，极限平衡状态对应的上拔力为极限上拔荷载，图2所示的极限上拔荷载为790 kN。利用《架空送电线路基础设计技术规定》中原状掏挖基础上拔承载力计算的剪切法中的通用公式进行计算［6］，上拔荷载为900 kN，比本文FEM法计算结果高约13%，说明本文计算结果可靠。ALE算法中，可以调节相应的参数，自行选择n次分析步时，对所选区域处重新划分网格，本次计算中相关调节参数均为默认值。当位移载荷达到0.2 m时，变形后的网格如图3所示。通过观察可以看出，虽然土体产生了较大变形，但模型中的网格并没有出现畸变现象。因此可以说明，ALE算法可以很好的解决扩底桩上拔状态下土体的大变形问题。

当桩基承受上拔荷载时，桩端扩大头开始处剪应力最大，其附近最先出现塑性区，随着荷载的增加，塑性区沿着扩大头变截面向两侧开展。图4和图5分别为扩底桩在极限状态下的广义剪应力和等效塑性应变云图。等效塑性应变超过5%的区域以红色显示，由图5可见，扩底桩达到极限上拔承载能力时，桩周土体的破坏滑裂面为由桩底开始向两侧贯通至地面的类似双曲线的滑动面，这与输电线路原状掏挖基础上拔荷载作用下的破坏模式一致［6，7］。为更清楚地了解土体的变形特征，图6为极限状态下的位移矢量图。

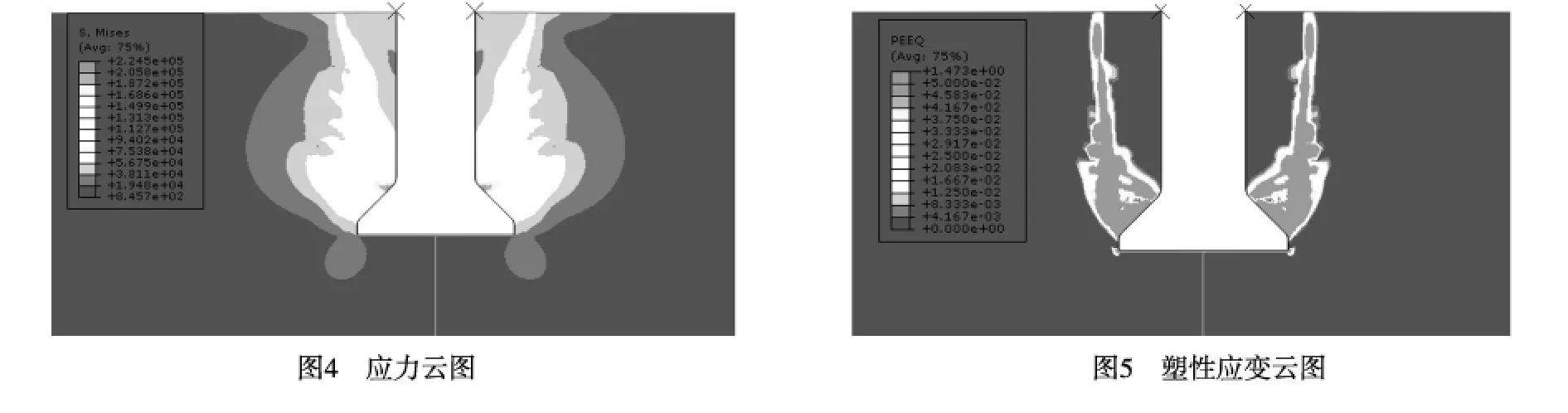
图6 位移矢量图

4 结 论

本文利用ALE法对扩底桩的上拔承载力进行了有限元分析，解决了扩底桩在承受上拔荷载情况下，土体网格由于变形过大而产生严重的网格畸变，结果收敛性较差的问题。数值计算结果给出输电线路掏挖基础承受上拔荷载时应力、应变及位移的变化趋势，桩周土体滑裂面开展过程，并将极限抗拔荷载与规范推荐方法比较，验证了基于ALE法的有限元计算结果的可靠性。因此，可以利用该方法继续分析非均质土中及同时承受水平及上拔荷载等复合加载模式下的扩底桩承载力研究。

［1］王俊林，王复明，任连伟，等.大直径扩底桩单桩水平静载试验与数值模拟［J］.岩土工程学报，2010，32(9):1406-1411.

［2］王凤池，王明恕.大直径扩底桩墩的工作机理和承载力设计［J］.岩土工程学报，2002，24(2):251-253.

［3］蒋建平，高广运，顾宝和.扩底桩、楔形桩、等直径桩对比试验研究［J］.岩土工程学报，2003，25(6):764-766.

［4］邓洪亮.扩底桩深度效应数值解法及其承载力确定方法［J］.岩土力学，2002，23(1):97-102.

［5］高广运，张蕾，滕延京，等.一种确定大直径扩底桩极限荷载的新方法［J］.岩土工程学报，2010，32(2):55-58.

［6］《架空送电线路基础设计技术规定 》(DL/T 5219—2005)［S］.北京:中国电力出版社，2005.

［7］Pacheco M P，Danziger F A B，Pereira Pinto C.Design of shallow foundations under tensile loading for transmission line towers:an overview［J］.Engineering Geology，2008，101(10):226 -235.