高压输电塔线体系覆冰的研究现状与展望

刘春城，刘法栋，毛绪坤，李霞辉

(东北电力大学建筑工程学院，吉林吉林132012)

覆冰作为一种特殊的气象条件，曾给世界各地许多架空线路的安全运行造成严重影响。输电线路所处的环境复杂，低温、冻雨、湿雪、冰冻等天气会造成输电线路严重覆冰，引起覆冰闪络、断线、倒塔等电网灾害，导致供电线路瘫痪，给社会造成了巨大的经济损失［1-6］。

高压输电塔线体系由于在结构上日益趋于杆塔结构高耸、导线截面粗大、跨距长、高差较大等特点，覆冰对其影响更加严重;同时，高压输电线路的电压等级较高、载流量较大，线路破坏造成的经济损失巨大。有必要结合国内外输电塔线体系的理论研究和工程背景，展开系统的理论研究得到输电线路覆冰荷载引起的输电杆塔的破坏机理，协助有关部门完善架空输电线路的设计规范和确定加固方案，使输电线路具备抵抗大规模冰雪载荷的能力，从而保障在恶劣环境下电网的安全运行。

1 覆冰机理与类型

导线覆冰首先是由气象条件决定的，是受温度、湿度、冷暖空气对流、环流以及风等因素决定的综合物理现象。这些因素的不同组合确定了导线覆冰的形状、密度及厚度。而输电线路产生覆冰的必要气象条件是:①具有足可冻结的气温，即0℃以下;②空气中具有过冷却水滴或云雾;③空气相对湿度在85﹪以上;④具有可使空气中的过冷却水滴或过冷却云粒产生运动的相应风速，即:风速＞1 m/s［1］。另外，线路的海拔高度、导线悬挂高度以及覆冰发生的凝结高度，也会对线路覆冰产生影响。不同条件的组合将在导线上形成不同类型的覆冰。

通常根据电力系统运行、维护及设计要求，输电铁塔和导线的覆冰可以分成以下几类［7］:

雨凇，一般是由水滴直径较大的过冷却雨或毛毛雨在导线的迎风面形成的清澈光滑透明的覆冰，是在冻雨期发生于低海拔地区的覆冰。持续时间一般较短，坚硬，粘附力很强，冰的密度很高，约为0.9～0.92 g/cm3，因其密度大，产生的机械负荷也最大。雨凇覆冰是混合凇覆冰的初级阶段，输电塔和输电导线覆冰为纯粹的雨凇覆冰的情况相对较少［8］。

混合凇，通常是过冷却水滴在导线的迎风面形成的雨淞与雾淞交替混合冻结形成的不透明或半透明覆冰。形成时间较长，坚硬，粘附力强。混合凇的密度较高，约为0.6～0.9 g/cm3，混合凇生长速度较快，对输电塔和输电导线危害特别严重［9］。

雾凇，是由于山区低层云中含有的过冷水滴，在温度极低和风速较小的情况下形成的放射状的结晶。密度小于0.60 g/cm3，粘附力很弱，对输电塔和输电导线一般不构成威胁。

白霜［10］，是空气中的湿气与0℃以下的冷物体接触时，湿气在冷物表面凝结形成的。白霜粘附力弱，密度为0.05～0.3 g/cm3。对导线威胁不大，但会增加输电线路的电晕损失。

雪和雾，是由自然降雪粘附在输电线路上经过多次融化和冻结，成为雪和冰的混合物。有干、湿雪之分，可以达到相当高的质量和体积。

按覆冰的形成机理及形成过程，导线覆冰增长过程可分为两种:干增长和湿增长［11-13］。导线覆冰后的冰表面水滴部分冻结的覆冰过程称为湿增长覆冰，湿增长过程一般有冰凌形成;导线覆冰后的冰表面水滴完全冻结的覆冰过程为干增长覆冰，干增长覆冰密度小于纯冰的密度，一般无冰凌形成。一般来说，雨淞和湿雪是湿增长过程;而雾淞和干雪是干增长过程;混合凇则是干、湿增长交替进行的过程。但实际上，覆冰过程中条件是不断变化的，大多数情况下导线覆冰为混合凇。我国北方冬季气候干燥，输电线路上主要为积雪;而南方冬季低温天气时多产生冻雨，雨淞在输电线路上易形成密度较大且不宜脱落的覆冰。

2 覆冰预测模型研究

以有关气象数据为依据，通过理论模型来预测雨淞覆冰荷载的研究工作已进行50多年。期间，提出了许多使用气象数据的导线雨淞雾淞覆冰计算公式和模型，对覆冰预测模型的研究已由简单模型发展到复杂模型及雨凇雾凇混合冻结的数值计算模型，一些模型实现导线覆冰的预测已有相当的精度。

Imai［14］认为覆冰强度由导线表面的传热控制，是湿增长过程。单位时间单位长度上的雨淞量与空气温度(-T)成正比，而与降水强度无关。

式中:C1、C2为常数;V为风速;R为覆冰后的导线半径;T为气温;t为覆冰时间。

这个简单模型在概念上是正确的，但是覆冰表面的热量传递受到表面粗糙度及蒸发冷却的影响很难准确确定。在气温低于 -5℃ 时会高估导线覆冰量，而在气温接近0℃ 时会低估覆冰量，在极端情况下将低估覆冰量。

Lenhard［15］提出了一个最简单的冰重计算式，每米长导线的冰重M为:

式中:Hg为整个覆冰过程中的降水量;C3、C4为常数。

此模型只牵涉到一个降水量的气象参数，而忽略了风速、气温、湿度等对覆冰的影响。此模型的物理意义不清楚，且过于简单。

Goodwin［16］认为所有撞击到导线表面的液滴全部冻结，即覆冰为干增长过程，则单位长度导线的覆冰率为:

式中:W为空气中的液态水含量;Vi为液滴的撞击速度。

此模型假设导线上的覆冰为均匀圆筒形冰，且导线对水滴的收集系数为1。但模型计算中需要液滴下落速度的准确值很难确定。

Chaine［17］假设覆冰形状为不均匀的椭圆形，且为干增长过程。当实际覆冰导线截面为非椭圆形时，引入截面形状修正系数K，则覆冰的当量径向厚度为:

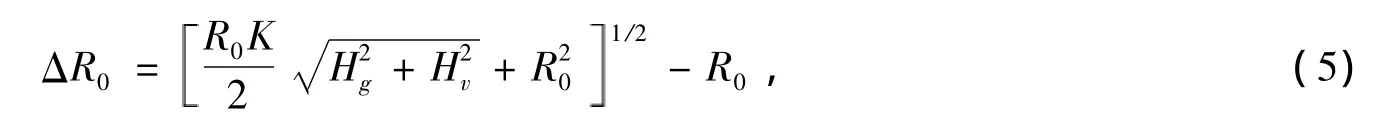
式中:修正系数K是导线半径R0及气温T的函数，由经验确定。

此模型不是用风速和液水含量来计算降水量，而是使用了水流量假设，与其他模型的值相差较远。

Makkonen［18，19］把导线半径、气温、风速、降水率、风吹角度及覆冰时间等作为输入量，用数值计算方法对这种考虑冰柱生长的覆冰模型进行了分析和计算。Makkonen在分析冻雨覆冰的湿增长过程中发现，导线上未冻结的液体并没有全部掉落，而是在导线的底部长成冰柱，而其他模型均未考虑覆冰过程中的这一物理特点。尽管此模型中的液态水含量和水滴大小分布参数不易测量，但其试验效果十分理想。

刘和云［20，21］在分析冻雨降水产生覆冰的物理过程后，提出了当过冷却水滴的直径d取为μm单位时，导线上均匀覆冰时的厚度ΔR可表示为:

式中:V为风速;P为降水率;N为冻雨的小时数;ti为第i个时间段的长度。

将此模型的预测结果与Imai模型、Lenhard模型、Goodwin模型等复杂模型的预测结果进行了比较，发现此简单模型取得比较满意的预测结果。但这些分析都没有考虑不均匀覆冰和风荷载的影响，有可能高估了输电塔结构的抗覆冰能力。

这些模型在预测同一气象条件下产生覆冰的冰重时会出现相差较大的预测结果。因为:①对覆冰时物理模型的细节假设上有差别，如覆冰是干增长还是湿增长过程，均匀覆冰还是非均匀覆冰等;②在经验数据的选取上不同，如空气中含湿量与降水率的关系，风速随高度变化的规律等;③在需要的气象参数选取上有所区别，如有的模型需要风速、空气湿度、降水率、空气温度等，而有的模型只需要其中的2～3个气象参数。

3 塔线体系覆冰断线的理论、模型试验、数值分析研究

3.1 理论分析

上世纪中期，世界各国研究人员通过不断努力，在覆冰研究领域取得了许多成果，输电线路覆冰研究取得了重大进展。

K.F.Jones等［22］在导地线径向均匀覆冰模型的基础上，提出了角钢铁塔的均匀覆冰数学模型，给出了计算公式，计算了不同截面形状的一致均匀覆冰厚度。简单形状结构上均匀覆冰厚度为t的覆冰面积A(t)为:

式中:t为覆冰厚度;L为角钢肢长;q、m为形状参数。

圆柱形结构上均匀覆冰厚度为tc的覆冰面积Ac(tc)为:

式中:l为导线的单位长度;α1、α2、α3分别为水滴在导线表面的碰撞、收集和冻结率。

刘纯［6］等对湖南500 kV复沙线倒塔段应用有限元计算程序建立单元模型，计算出铁塔随导线覆冰厚度变化的极限承载力，并分析了改事故段铁塔倒塌的原因。陆佳政等［6，13］对500 kV输电塔线覆冰进行了有限元分析计算。

H.Max Irvine［24］系统的研究了索结构的静力和动力特性，就两端固定索的动力特性进行了分析，采用连续体模型，在考虑缆索刚度与不考虑缆索刚度的情况下对索塔结构进行动力响应分析。该方法精度较高，常用来检验离散化模型的计算结果。

李宏男等［25，26］以湖南地区挂靖线220 kV输电线路覆冰倒塔为例，建立精细化输电塔线体系有限元模型，依据三峡地区覆冰资料建立覆冰增长曲线，考虑水平垂直档距、高差、不均匀覆冰和风荷载影响，对覆冰和风荷载作用下输电塔线体系进行非线性屈曲分析，计算出覆冰荷载以及风荷载与覆冰共同作用下输电塔结构的极限承载能力，分析了倒塔的主要原因。

S.Ozono等［27］在大量试验分析的基础上，提出了求解输电塔线耦合体系平面动力特性的计算模型，分析了塔线跨数、边界条件、导线的质量和垂跨比对塔线体系对平面动力特性的影响，探讨了塔线耦合对输电塔和导线振型的影响。

Nigol等［28］初步建立了覆冰导线运动稳定性分析的理论与方法，该理论认为，舞动是由导线自激扭转引起的。Nigol扭转舞动理论不仅考虑了偏心覆冰导线在风激励下的空气动力特性，还考虑了导线扭转的影响。

Roshan Fekr等［29］则对档距为200 m的输电线路的脱冰过程进行了数值模拟，通过改变单元密度的方法对二十一种典型覆冰及脱冰工况进行了模拟，得出了覆冰厚度和脱冰位置等对输电线路的影响。

李黎、夏正春等［30］用有限元方法模拟导线断线和脱冰跳跃对体系的动力响应，建立了导线模型，并以等效弹簧代替导线对输电塔作用的塔-弹簧模型，将导线在断线作用下悬垂点的支座反力反向施加在塔-弹簧模型上，数值仿真了输电塔在导线断线作用下的动态响应。

侯镭等［31］针对特高压线路的脱冰跳跃，计算得到导线脱冰跳跃的时程响应，并分析了脱冰量、档距组合、导线机械参数、均匀与非均匀脱冰等因素的影响。周迪等［32］用半椭圆雾淞覆冰模型对导线在风力作用下的机械脱冰机理进行了分析研究，获得了最大剪切力及最大扭转角的计算方法和公式。

Yasui等［33］为检验不同支撑条件下(自立式和拉线式)输电塔线体系风振响应的差别，将输电塔简化为梁或桁架单元，将导线与绝缘子串简化为桁架单元，在时域内分析了结构的动力响应特性。

从输电线路的研究进展来看，对覆冰输电塔线体系方面的研究多是停留在对覆冰输电导线的单独研究上，并没有考虑输电塔本身和地线的覆冰以及覆冰后塔线之间的耦合作用。对导地线的覆冰只给出了均匀覆冰情况的力学模型，没有进一步考虑不均匀覆冰的影响，有可能高估了输电塔线体系的抗覆冰能力。

3.2 模型试验

高压输电塔动力响应的试验研究是近年来才开展起来的，主要包括风洞试验和现场实测等研究手段。

Morgan等［34］对一132 kV的五档输电线路作了一系列试验，通过在档中点释放固定载荷来模拟脱

式中，tc为覆冰厚度;d为垂直于雨滴轨迹的截面直径。

蒋兴良［1，2，23］等人根据对鄂西及川东地区输电线路因导线覆冰引起事故的调查结果，分析了三峡地区输电线路导线覆冰的基本特征，并从理论上建立了导线的雾凇覆冰模型。单位时间dt内雾凇增加的质量dM可表示为:冰过程，并测出了各档的跳跃高度。

Stewart［35］通过实验来说明了覆冰对输电线路的影响。Jamaleddine等［36］在人工气候实验室对一个两档的输电线路的缩小模型做了多种脱冰工况的模拟，通过等效系数的换算可以将试验结果用到实际的输电线路中去，而且还对所使用的试验模型进行了数值模拟，模拟结果和实验结果吻合。

Loredo-Souza等［37］通过修正模型试验法，初步解决了风洞试验中模型设计难以同时满足相似定律和风洞尺寸要求的问题，在导线气动阻尼、风向变化效应和平行导线相干系数等方面取得了一些有价值的研究成果。

楼文娟等［38，39］以椒江大跨越直线塔为背景，对输电塔线体系在静态风作用下的顺风响应和脉动风作用下的横风向及顺风向响应进行了试验测试，并考虑了风速、风向角等因素的影响，提出了输电塔架横风响应的简化计算方法。

邓洪洲等［40，41］以江阴输电塔线体系为背景，在均匀流场和紊流场中分别对单塔和塔线体系进行了不同风速下的风振试验研究。结果表明，导线对塔架自振频率影响不大，但塔线体系的阻尼较单塔有显著提高;单塔和塔线体系在均匀流场和紊流场的风振响应谱各阶频率值的大小随风速变化不大，但随着风速的增加，功率谱曲线频谱成分变得饱满，体系的非线性影响逐渐加强。

气象参数对电力线路覆冰雪有着决定性的影响，日本在一个风洞设施开展试验研究［42］，监测单位时间内围绕导线的雪花分布、风速、湿度、温度、雪花中的液态水含量、单位长度导线积雪分量、导线旋转角度、试验持续时间以及运行导线表面温度等参量，并分析了各种气象参数对冰雪的影响。

李宏男等［43，44］根据某输电塔现场观测数据，采用模态识别技术对输电塔和输电塔线体系的动力响应特性进行了反演，并与数值分析的结果进行了对比，从而验证了数值方法的正确性;采用数据统计分析与理论模拟的方法分别计算阵风响应因子，并对阵风响应因子的敏感性影响因素进行了识别与分析。研究表明:输电塔的准静态阵风因子法是结构设计分析的有效方法，具有较好的计算精度。

王肇民等［46］对塔架的静力性能和动力性能都进行了大量的开拓性的研究工作，并考虑了杆件初始缺陷及几何和材料非线性，取得了许多成果。

还有一些学者也应用有限元原理开发了一些输电塔结构分析软件，如东北电力设计院在1985年开发了《多塔高、多接腿送电塔满应力设计软件》;原电力部的电力建设研究院等单位对输电塔架进行了不少仿真试验研究，得到了许多数据资料和有益结论。

4 存在的问题及展望

(1)目前有关覆冰的研究仍存在很多困难:例如对水的物理特性、雪的快速变态、积雪机制的多样化等因素的研究只能在实验室进行，人工实验结果并不理想。有必要设计新方法进行自然积冰雪的研究，积累现场数据，分析覆冰和气象参数之间的关系。

(2)关于覆冰模型的研究。尽管国内外提出了几种雨凇覆冰模型，如刘和云建立的简单模型，虽然比较全面的考虑了各种气象参数的影响，但是其模型没有考虑非均匀覆冰的情况，因此需要对该模型进行修正;没有按不同地区的气象条件给出模型的确切公式;对于档内及相邻档沿导地线方向的不均匀覆冰缺乏研究。

(3)目前国内外缺少关于输电塔覆冰模型的研究，输电塔覆冰后弹性模量、刚度等参数会发生变化，和只考虑导地线覆冰，不考虑输电塔覆冰的情况有较大差别。此外，研究塔线体系覆冰断线时，应考虑塔线体系的耦合作用，以及如何计算其耦合影响。

(4)目前国内外关于导地线断线的研究只是针对覆冰时的风荷载、覆冰舞动、脱冰跳跃等情况分别研究，没有考虑到这些因素之间的组合对断线的影响。

(5)关于高压输电塔线体系覆冰断线的现场实测和模型实验研究以及覆冰断线造成输电塔倒塔的动态全过程数值模拟还有待完善。

［1］蒋兴良，易辉.输电线路覆冰及防护［M］.北京:中国电力出版社，2002.

［2］苑吉河，蒋兴良，易辉，等.输电线路导线覆冰的国内外研究现状［J］.高电压技术，2004，30(1):6-9.

［3］杨靖波，李正，杨风利，等.2008年电网冰灾覆冰及倒塔特征分析［J］.电网与水力发电进展，2008，24(4):4-8.

［4］胡毅，胡建勋，刘庭.我国南方地区电网大范围覆冰灾害的特点分析与防治措施［J］.电力设备，2008，9(6):1-4.

［5］胡毅.电网大面积冰灾分析及对策讨论［J］.高电压技术，2008，34(2):215-219.

［6］刘纯，陆佳政，陈红冬.湖南500kV输电线路覆冰倒塔原因分析［J］.湖南电力，2005，25(5):1-3.

［7］Daisuke Kuroiwa.Icing and Snow Accretion［M］.Monograph series of the research institute of applied electricity，1958.

［8］Makkonen L.Atmosphric Icing on Structure［J］.U S Army CRREL Monograph，1984，84(2):102 - 105.

［9］Macklin W C.The Density and Structure of Ice Formed by Accretion［J］.Quart J Roy Meteor Soc，1962(8):30 -50.

［10］Lahti K，Lahtinen M.Transmission Line Corona Losses under Hoar Frost Conditions［J］.IEEE Trans on Power Delivery，1997，12(2):928 -933.

［11］蒋兴良，马俊，王少华，等.输电线路冰害事故及原因分析［J］.中国电力，2005，38(11):27-30.

［12］蒋兴良.输电线路导线覆冰机理和三峡地区覆冰规律及影响因素研究［D］.重庆:重庆大学，1997.

［13］陆佳政，蒋正龙，雷红才，等.湖南电网2008年冰灾事故分析［J］.电力系统自动化，2008，32(11):16-19.

［14］Imail.Studies on ice accretion［J］.Researches on Snow and Ice，1953，3(1):35 -44.

［15］lenhard R W.An indirect method for estimating the weight of glaze on wires［J］.Bull.Amer.Meteor.Soc，1955，36(3):1 - 5.

［16］Goodwin E J，etal.Predicting ice and snow loads for transmission lines.Proceedings［C］.First IWAIS，1983:267 -273.

［17］Chaine P M，Casfonguay G.New approach to radial ice thickness concept applied to bundle like conductors［R］.Industrial Meteorology study IV，Environment Canada，Toronto，1974，11.

［18］Makkonen L.Estimating intensity of atmospheric ice accretion on stationary structure［J］.Journal of Appliced Meteorology，1981，20(5):595-600.

［19］Makkonen L.Modeling power line icing in freezing precipitation［C］.7th International Workshopon Atmospheric Icing of Structures，1996，Canada.195 -200.

［20］刘和云.架空导线覆冰防冰的理论与应用［M］.北京:中国铁道出版社，2001.

［21］刘和云，周迪，付俊萍，等.导线雨凇覆冰预测简单模型的研究［J］.中国电机工程学报，2001，21(4):44-47.

［22］K.F.Jones，A.B.Peabody.The application of a uniform radial ice thickness to structural sections［J］.Cold Regions Science and Technology，2006，44(2):145 -148.

［23］孙才新，蒋兴良，熊启新，等.导线覆冰及其干湿增长临界条件分析［J］.中国电机工程学报，2003，23(3):0141-0145.

［24］Irvine H.M.Cable Struetures［M］.Cambridge:MIT Press，1981.

［25］李宏男，白海峰.高压输电塔线体系抗灾研究的现状及发展趋势［J］.土木工程学报，2007，40(2):39-46.

［26］李雪，李宏男，黄连壮.高压输电线路覆冰倒塔非线性屈曲分析［J］.振动与冲击，2009，28(5):111-114.

［27］Ozono S.and Maeda J.In Plane Dynamic interaction between a tower and conductors at lower frequencies［J］.Eng.Structures，1992，14(4):210-216.

［28］O.Nigol，P.G.Buchan.Conductor Galloping.1.Den Hartog Mechanism［J］.IEEE Transactions on Power Apparatus and Systems，1981，100(2):699-707.

［29］M.Roshan Fekr.G.McClure.Numerical modeling of the dynamic response of ice - shedding on electric transmission lines［J］.Atmosphericc Research，1998，46(1/2):1 -11.

［30］李黎，夏正春，等.输电塔在线路断线作用下的动力响应［J］.振动与冲击，2007，26(11):45-49.

［31］侯镭，王黎明，朱普轩，等.特高压线路覆冰脱落跳跃的动力计算［J］.中国电机工程学报，2008，28(6):1-6.

［32］周迪，素逸.覆冰导线风动脱冰研究［J］.长沙电力学院学报(自然科学版)，2002，17(2):54-56.

［33］Yasui H，Marukawa H，Momomura Y，Ohkuma Y.Analytical study on wind - induced vibration of power transmission towers［J］.Journal of Wind -Engineering and Industrial Aero - dynamics，1999，83(1):431 -441.

［34］V.T.Morgan.D.A.Swift.Jump height of overhead - line conductors after the sudden release of ice loads［J］.Proceedings IEE 1964，111(10):1736-1746.

［35］J.R.Stewart.Ice as an influence on compact line phase spacing［J］.Proceedings of IWAIS，Hanover，Mew Hampshire，1983:77 -82.

［36］G.McClure.J.Rousselet.R.Beauchenmin.Simulation of Ice - shedding on electrical transmission lines using ADINA［J］.Computers and Structures，1993，47(4/5):523 -536.

［37］Loredo - Souza A M，Davenport A G.A novel approach for wind tunnel modeling of transmission lines［J］.Wind Eng.Ind.Aerodyn，2001，89(11/12):1017-1029.

［38］楼文娟，孙炳楠.风与结构的耦合作用及风振响应分析［J］.工程力学，2000，17(5):16-22.

［39］楼文娟，孙炳楠，唐锦春.高耸格构式结构风振数值分析及风洞试验［J］.振动工程学报，1996，9(3):108-112.

［40］邓洪洲，朱松晔，王肇民.大跨越输电塔线体系动力特性及风振响应［J］.建筑结构，2004，34(7)，25-28.

［41］邓洪洲，朱松哗，陈晓明，等.大跨越输电塔线体系气弹模型风洞试验［J］.同济大学学报，2003，31(2):132-137.

［42］Sakamoto Y.Snow accretion on overhead wires［J］.Philosophical Transactions of the Royal Society，2000，358(1776):2941 -2970.

［43］李宏男，石文龙，贾连光.导线对输电塔体系纵向振动的影响界限及简化抗震计算方法［J］.振动与冲击，2004，23(2)1-7.

［44］李宏男，任月明，白海峰.输电塔体系风雨激励的动力分析模型［J］.中国电机工程学，2007，27(30):43-48.

［45］王肇民.桅杆结构［M］.北京:科学出版社，2000.