龙卷风作用下空间桁架的受力分析
2011-06-13白俊峰鞠彦忠
白俊峰,鞠彦忠,曾 聪
(东北电力大学建筑工程学院,吉林吉林132012)
龙卷风是一种伴随着高速旋转的漏斗状云柱的强风涡旋,中心附近风速可达100 m/s~200 m/s,最大300 m/s。中心气压很低,一般可低至400 hPa,最低可达200 hPa。龙卷风发生的概率低于其他极端风,因此除了损坏的后果特别严重的核电站建设要考虑龙卷风外,其他建筑规范与标准中尚未包含龙卷风设计的要求[1-3]。
但随着结构风工程领域的发展和日益增多的龙卷风灾害,国外一些学者已经开始研究龙卷风对结构的作用。风作为空间桁架结构的控制荷载,本文分析龙卷风作用下空间桁架结构的受力情况,提出荷载处理方法和加载方式对结构防灾减灾具有重要意义。
1 龙卷风风场数值模型
龙卷风像一个以一定速度平移的高速旋转的圆筒,风场结构非常复杂,但可以用相互一致的参数组:切向风速、径向风速、竖向风速和平移风速以及最大切向风速半径(rmax)和气压变化来表征。各参数大小以分布见图1,图中虚线为龙卷风边界层,边界层以上的风速和边界层内部的风速分布不同。
1.1 龙卷风风场理论模型
龙卷风作为气流的特殊运动是一种涡旋和急流的叠加运动[4],兰金复合涡(Rankine- Combined Vortex)作为二维定常轴对称涡,是一种在物理上更现实和更具普遍性的模型[5]。兰金(Rankine)在1882年提出了复合涡模型,他把流场分成两个区域。内部区域速度同半径成正比,外部区域同半径成反比。其表达式如下:
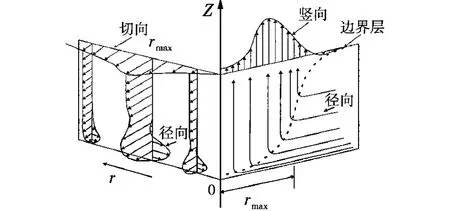
图1 龙卷风结构和风速分量示意图
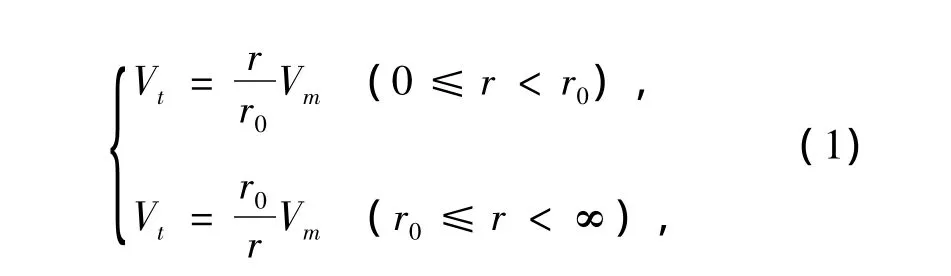

图2 兰金涡流的速度分布
式中:Vt为风场中任一点的切向速度;Vm为最大切向速度;r0为最大切向速度对应的半径;r为任一点距龙卷风中心的距离。
图2给出了兰金涡的速度分布,本质上是一个无粘性涡旋模型,其中涡核内外的速度分布在r0处不是一种光滑过渡,这是没有涉及粘性效应的结果。事实上,在粘性作用下,这种过渡必定是光滑的,并且涡量要向外扩散,使涡核的半径随时间增加。
1.2 龙卷风风场统计模型
许多科研人员根据大量气象和实测数据统计总结出龙卷风切向速度、径向速度、竖向速度和平移速度的大小关系,其中Vr为径向速度、Vv为竖向速度、Vm为切向速度、Vt为平移速度、Vs为水平最大速度、Vro为旋转速度。各分量有如下关系[6,7]:
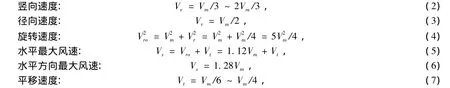
1.3 基于兰金复合涡流模型的龙卷风风险度模型
我国1991年4月26日国家核安全局批准发布的《核电厂厂址选择的极端气象条件》(HAD101/10)[8]对龙卷风有相关规定和论述:基于兰金复合涡流模型的龙卷风风险度模型被认为比别的模型更接近实际,因为它考虑了破坏带横断面的不同破坏程度,可以确定某个区域确定的面积——强度关系,计算局部区域内某个点遭受给定风速范围内某一风速的概率。由于破坏力是由风速的平方决定的,所以破坏宽度同风速有一定的关系。
为了获得局部区域超过某些阀值风速的某一风速的概率,要把面积—强度和事件—强度关系与组合兰金涡流风速分布结合起来考虑,图3说明了受破坏宽度与风速大小的关系,假定在最大风速半径以外的分布为组合兰金涡流模型(即V×R=常数)。在这种风险模型中的平均破坏面积假定是由等于或大于33.5米/秒的风速造成的破坏面积。利用兰金复合涡流模型最大风速边界层以外的速度分布关系式有:

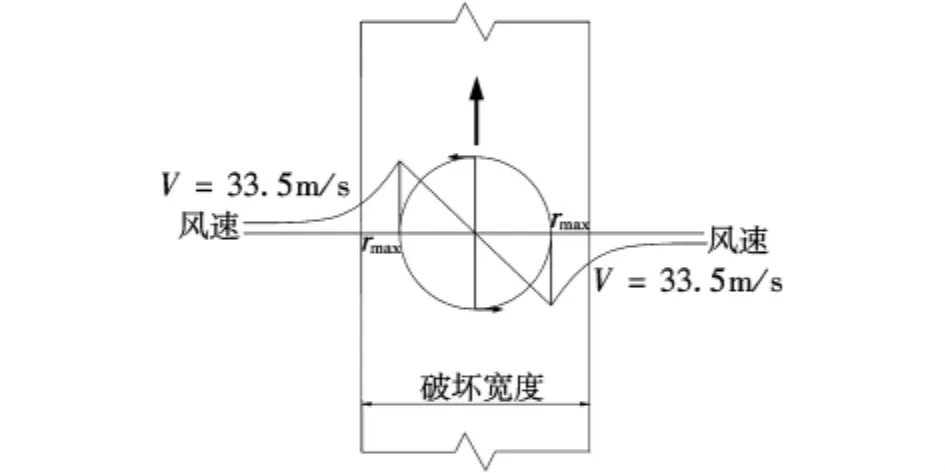
图3 龙卷风风险度模型中破坏宽度示意图
式中:Rd为最大破坏半径。
1.4 龙卷风风场半经验模型
Wen Y.K提出用龙卷风风场半经验公式用来计算龙卷风的风场特性[9]。描述龙卷风的基本参数有最大风速矢量,旋转风速矢量,平移风速矢量,旋转中心总压降 △p,压降速率和最大切向风速对应半径RM。各参数之间的关系如下:


式中:ρ为空气密度,一般取1.225,龙卷风的边界层厚度为:

其中:r=r'/rm,r'为模拟点距龙卷风中心的距离,rm为最大切向风速对应的半径,δ0为r=1m处大气边界层厚度;龙卷风边界层厚度随半径变化曲线见图3,龙卷风风速按下列公式计算:
(1)边界层以外风速为:

(2)边界层内部风速为:
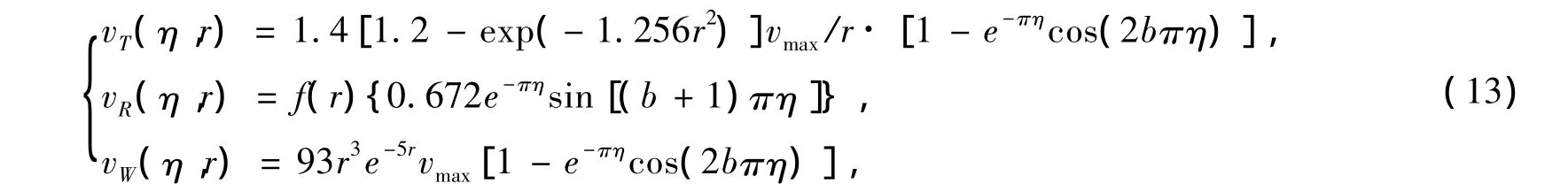
式中:vT(η,r)为切向风速;vR(η,r)为径向风速;vW(η,r)为竖向风速;vmax为最大切向风速;b为r的函数,b(r)=1.2e-0.8r4;η=z/δ,z为模拟点离地面高度;δ为对应模拟点的边界层厚度。龙卷风半经验公式风压分布图见图1。
2 龙卷风对结构的作用
Emil Simiu和Robert H.Scanlan[10]将龙卷风对结构的作用分为三部分:
(1)由气流直接作用在结构上引起的风压。
(2)当龙卷风刮过结构物时,大气压力场突然变化所引起的压力(气压变化效应),如果建筑物不能充分通风使内外压力迅速平衡,就可能引起爆炸。
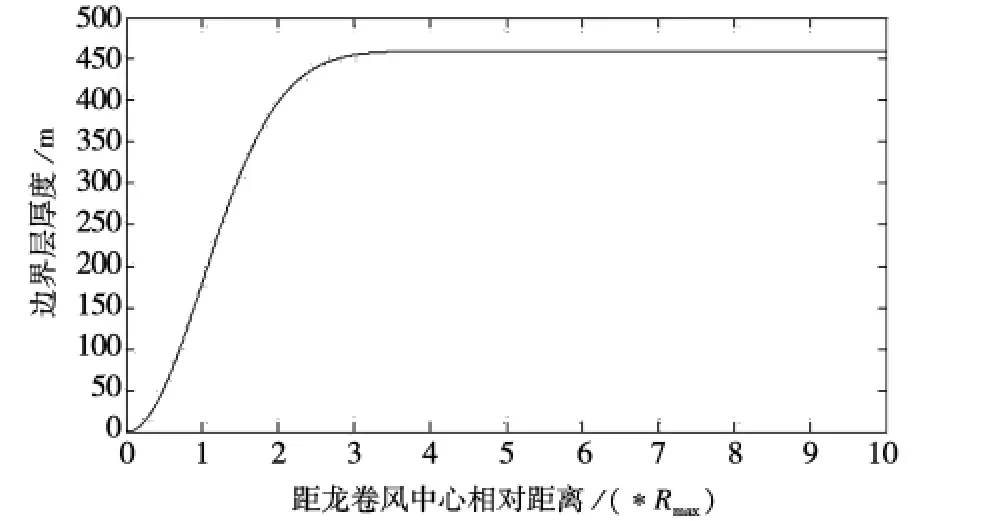
图4 边界层厚度变化曲线
(3)龙卷风飞掷物引起的冲击力。
若结构物无开孔(密闭结构),则龙卷风通过前,结构内部压力保持与大气压力相等。因此龙卷风通过期间,结构物内压与大气压力之差为龙卷风的气压降;若结构物是完全敞开的,则在实用上认为内压与外压瞬间平衡了,于是由大气压变化引起的荷载接近于零。由于空间桁架结构属于开放式结构,不存在密闭结构产生的气压差。并且在挡风面积很小,小尺度龙卷风吹起的飞掷物(包括雨、冰雹、沙砾等)都很小,对结构产生的影响可以通过一个风压提高系数来考虑。

图5 切向风速度分布
3 实例分析
2008年05月23日19时10分黑龙江省五常市遭受龙卷风袭击,根据现场目击者描述和灾害损坏现象及程度估计龙卷中心风力达到16~18级,瞬间风力达到50 m/s左右,地面破坏宽度为50 m左右,按Fujita龙卷风等级表所述属于F1级中龙卷。
由龙卷风风场统计模型可以得到龙卷风最大切向速度为40 m/s,由50 m破坏宽度结合风险度模型可知破坏为半径25 m,最大切向风对应的半径是21 m。
切向速度分布及基本风压分布见图5,龙卷风切向速度分布为:


图6 切向风基本风压分布
作用在结构上的基本风压为:
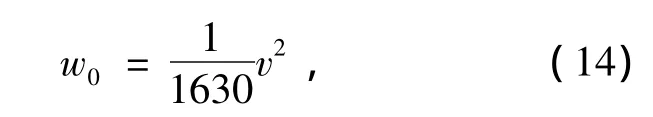
则切向风的基本风压分布见图6。
根据龙卷风统计模型得到各龙卷风分量的大小为:径向风速:Vr=Vm/2=20 m/s;竖向风速:Vv=2Vm/3=80/3(m/s);平移速度:Vt=7Vm/29=9 m/s。
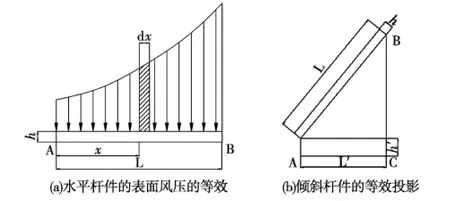
图7 杆件风压等效节点力示意图
由图6可知龙卷风风场在3倍最大切向风对应半径的范围内,分压分布很不均匀。当小尺寸结构,像输电铁塔、通信塔等高耸桁架结构,考虑结构各根杆件处于龙卷风风场中的不同位置,所受水平向风力也不相同,而区别于自然风对桁架结构相对均匀的作用。因此要提出杆件表面有龙卷风这样不均匀荷载作用下的荷载处理方法和加载方式。并结合龙卷风半经验模型得到竖向风压和径向风压区域分布及数值大小。
为了使计算结果精确,更接近于实际桁架结构的受力情况,必须考虑每根杆件表面不同的风压分布,对每根杆件的风压都要等效成杆端的节点集中力。
建立龙卷风的兰金复合涡流模型后,得到切向风压分布。建立风场中迎风面每根杆件杆端的相对坐标,根据相对位置得到每根杆件表面对应的风压,将非均匀分布荷载等效为杆端节点集中力。图7(a)中,假设杆件AB为输电塔中的水平杆件,A点坐标为(x1,y1),B点坐标为(x2,y1),利用弯矩平衡原理,则A、B等效杆端节点力fA、fB为

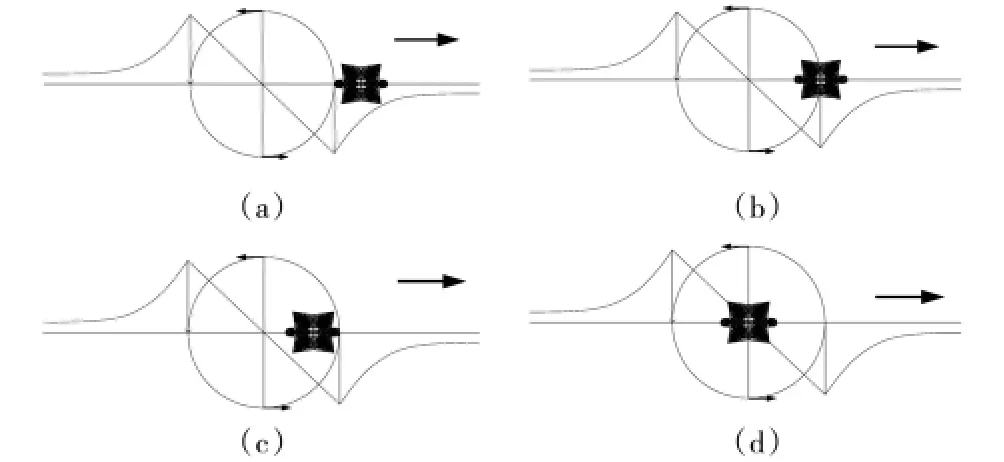
图8 输电塔在龙卷风风场中的四个典型区域
但是对于输电塔迎风面中绝大多数杆件来说,都是倾斜放置的见图7(b)中的AB。通过水平投影和面积等效得到倾斜杆件的水平等效受力杆件AC(见图7(b)),就可以按照式子(15)、(16)公式进行等效节点力计算。
输电塔作为典型的空间桁架结构,具有数量大、分布广的特点,容易遭受龙卷风的袭击。以输电塔为例来分析桁架结构在龙卷风复杂风场中的受力情况。
通过图8分析可知:其中(a)(c)为输电塔在兰金复合涡两个区域中风压最大,表面风荷载不均匀的情况;(b)为输电塔水平方向风荷载最大时的情况,但是如果考虑涡的粘性扩散作用,输电塔实际在这个位置迎风面所受的风压是近乎均匀的,同自然风作用下的输电塔拟静力分析原理相同;(d)为龙卷风中心同输电塔中心重合时输电塔整体扭矩最大的情况,虽然内部风场结构复杂、风压分布极其不均匀,但属极小概率事件,可以不考虑。
大量有关龙卷风实测记录的外文文献[11,12]中都对径向风和竖向风给出了多普勒雷达测得云图和模拟结果图如图9所示,距地面20 m范围内有径向风作用,其大小为切向风风压的1/4。(c)位置的竖向风均匀加载到输电塔的每一个节点,(a)位置由于竖向风很小,因此忽略不计。
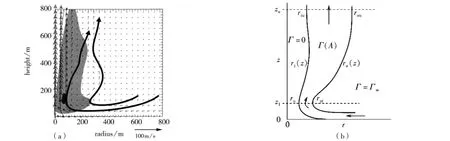
图9 多普勒雷达测得云图和模拟结果图
通过有限元软件的计算与分析,从图10、11可以看出输电塔位于龙卷风风场中(a)、(c)两个典型位置时的变形以竖向弯曲为主,铁塔扭转幅度很小;两个相对位置处输电塔出现最大拉、压应力的杆件分别位于塔身中段和塔腿处。本文还计算了35 m/s风速的自然风作用下输电塔的变形和内力,同龙卷风作用下输电塔的响应很相近。
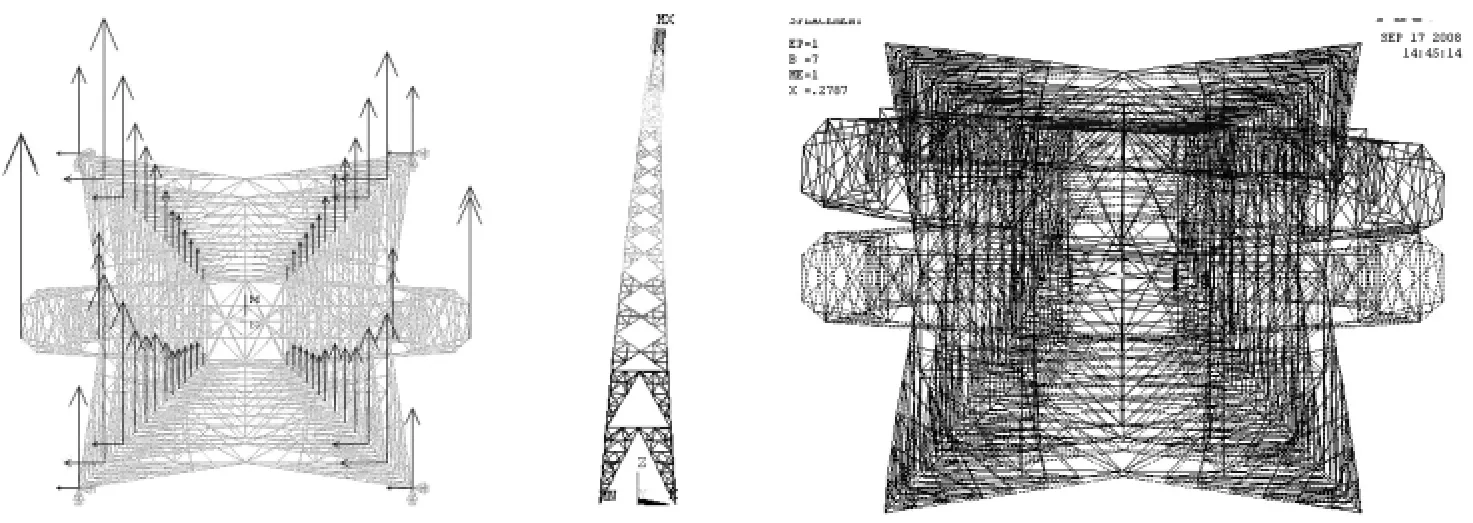
图10 (a)位置输电塔加载、变形以及图

图11 (c)位置输电塔加载及变形图
5 结 论
(1)首先介绍了龙卷风的风场结构,分析了龙卷风对桁架结构物的破坏形式;结合流体力学中的涡运动理论、大量实测数据的统计分析、Wen.Y.K.风场半经验公式和龙卷风风险度模型等理论及模型建立了适合空间桁架计算分析的龙卷风风场数值模型。
(2)并以2008年05月23日19时10分黑龙江省五常市发生的龙卷风灾害为研究背景,建立本次灾害中的龙卷风风场数值模型。
(3)分析了桁架在龙卷风作用下的受力情况,以及如何考虑作用在桁架结构上的龙卷风荷载,提出了荷载处理方法及加载方法。以空间桁架结构中最常见的输电塔为例进行了受力分析,得到了输电塔在龙卷风荷载作用下的变形以竖向弯曲为主,扭转幅度很小,塔身中段和塔腿处会出现较大的拉应力和压应力。
(4)通过与自然风静力响应的对比,可以认为在今后的设计和研究中。采用等效风速的自然风来计算龙卷风对空间高耸桁架结构的作用,以此来简化计算过程。
[1]Uniform Building Code[C],International Conference of Building Officials,Los Angels,Calif,1975.
[2]Southern Building Code,[S],Brimingham,Ala.,1965.
[3]American National Standard Building Code Requirements for Minimum Design Loads in Buildings and Other Structures[S],A58.1,American National Standard Institute,New York,1982.
[4]刘式适,付遵涛,刘式达等.龙卷风的漏斗结构理论[J].地球物理学报,2004,47(6):959-963.
[5]童秉纲,尹协远,朱克勤.涡运动理论[M].安徽:中国科学技术大学出版社,76-94
[6]K.C.Mehta,J.R.Mcdonald,J.Minor,Tornadic loads on structures[C].in:Hatsuo Ishizaki,Arthur N.C.Chiu(Eds.),Proceedings of the Second USA-Japan Research Seminar on Wind Effects on Structures,University of Tokyo,Tokyo,Japan,1976:15 -25.
[7]B.L.Agarwal,P.K.Dutta,A.K.Ghosh,Tornado at Nayagarh[R].Orissa,India:A report on June 2,1997.
[8]核电厂安全导则汇编[S].北京:中国法制出版社,2000:727-772.
[9]Wen Y K.Dynamic Wind Loads on Tall Building[J].Structure Division,ASCE.Jan 1975,101(ST1):169 -185.
[10]Emil Simiu,Robert H.Scanlan.Wind Effects on Structures[M].New York:JOHN WILEY & SONS,INC.1996:551 -575.
[11]D.C.Lewellen,W.S.Lewellen.Near- Surface Intensification of Tornado Vortices[J].Journal of the atmospheric sciences,2007,64(7):2176-2194.
[12]Howard B.Bluestein,Christopher C.Weiss,Michael M.French,Eric M.Holthaus,and Robin L.Tanamachi.The Structure of Tornadoes near Attica,Kansas,on 12 May 2004:High - Resolution,Mobile,Doppler Radar Observations[J].AmericanMeteorological Society.2007,135(2):475-506.
