基于ATmega64L的128点实时FFT

郭 刚,李 钊,李建军,胡礼勇,董巍巍

(1.第二炮兵青州士官学校,山东青州262500;2.第二炮兵驻石家庄地区军事代表室,河北石家庄050081)

0 引言

目前,以单片机为核心的手持式振动信号采集器配有简洁的信号调理和显示电路,能够完成低频振动信号的采集、储存和传输,成本低廉,在机器振动状况检测领域应用广泛。但受单片机硬件资源的制约,其一般不具备现场对采样数据进行FFT的能力[1,2]。然而,FFT是振动信号分析最常用的方法,对许多现场采集的信号数据,只需进行少量采样点的FFT,即可算出机器振动的主频,进而快速判断运转状态,实现对机器运行状态的快速检测和故障初诊,具有很大的实用价值。下面将着重阐述在以ATmega64L单片机为核心的手持式振动信号采集器上实现128点FFT的过程和方法。

1 按时间抽取基2FFT算法[3,4]

离散傅里叶变换(DFT)的本质就是建立了以时间为自变量的信号与以频率为自变量的频谱函数之间的变换关系。设X(n)为N点有限长序列,其DFT公式为:

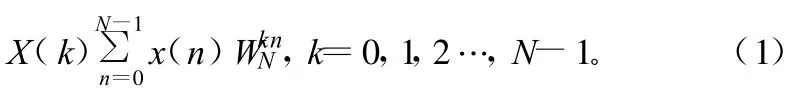
式中,

按时间抽取的基2FFT算法,利用旋转因子的对称性、周期性和可约性,根据输入序列时间上的奇偶,将一个N点的DFT分解成2个N/2点的DFT,再把2个N/2点的DFT又可按照奇偶分成2个N/4的DFT,直到最终分解为N/2个2点的DFT运算。本算法的基本运算单元是2点蝶形运算结构。当N=2M时(这里M为自然数),整个运算共有M级,每级又有N/2个蝶形运算组成。蝶形运算计算流程如图1所示。

图1 蝶形运算单元

蝶形运算方程式为:

在处理采集到的实际数据时,输入信号序列通常是实数。理论上使用N点复数FFT完成2N点实数序列FFT运算,可以提高运算速度并且减小存储空间。但是变换完成后的结果转化计算量较大,导致单片机整体运算速度不能显著提高,又鉴于ATmega 64L单片机自带 4 KB的 RAM,完全满足128个32位浮点数进行FFT的存储空间需求,所以此处直接使用128点复数FFT算法完成128个实数采样数据的FFT运算,在运算时要把原实数数据作为复数的实部,而对应复数虚部需全部置零。

2 ATmega64L单片机采集系统

该系统采用ATmega64L单片机作为控制核心。它是基于RISC结构的8位低功耗CMOS微处理器,大部分指令都可以在一个时钟周期内完成,最大可以支持16 MHz的系统时钟,片载64 KB的可编程Flash,2B的EEPROM,4KB的SRAM,53个通用I/O口线,32个通用工作寄存器和2个串口、SPI接口和TWI接口等丰富的外围接口电路。整个振动信号采集系统的硬件框图如图2所示。

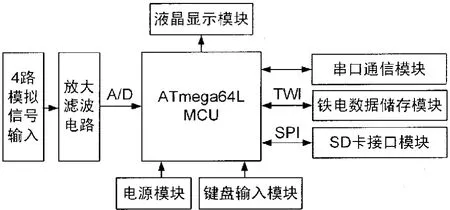
图2 采集系统硬件

3 128点采样数据实时FFT的实现

3.1 进行复数FFT计算的步骤及流程

使用ATmega64L单片机进行128点采样数据FFT计算时,应首先把输入的128个实信号虚部置零,使其变为复数,然后将数据序列按码位倒置的方式反序排列,再进行按时间抽取基2FFT运算,最后计算转换后各复数的模并比较分析振动信号主频,具体FFT计算流程图如图3所示。

图3 128点 FFT流程

3.2 在ICCAVR中编程实现FFT的要点

3.2.1 反序排列算法的实现

反序排列是由FFT算法的性质决定的。首先将128个数据点自然排列的十进制数转换成7位二进制数,再将这些二进制数的首位至末尾的顺序颠倒过来重新换算成十进制数,即得到反序排列的结果。为减小单片机的运算负担,同时充分利用ATmega64L程序存储器大的优势,使用MATLAB软件算出128点反序排列结果,并以数组形式存放在单片机程序存储器中,FFT运算时,单片机只需进行简单的查表,即可快速完成数据反序操作。单片机存储128个序列码为:

const unsigned char inv_tab[128]={0,64,32,96,16,80,……,47,111,31,95,63,127}。

3.2.2 旋转因子的计算和储存

进行FFT的子函数运算时,实时计算旋转因子的值,对单片机而言是十分繁重的任务。根据旋转因子的复数形式,预先算出 cos(2πkn/N)和sin(2πkn/N)的值(取小数点后4位精度),并以数组的形式存储在单片机的程序存储器内,供FFT运算过程中随时调用。单片机存储旋转因子实部和虚部的形式为:

const float cos _tab[64]={0,-0.0491,-0.0980,-0.1467,…,-0.9808,-0.9892,-0.9952,-0.9988};

const float sin _tab[64]={1,0.9988,0.9952,…,-0.1467,-0.0980,-0.049}。

3.2.3 FFT各级蝶形运算的实现

根据FFT算法的特性,使用3级循环完成各级蝶形运算[5]。

for(L=1;L＜=7;L++){//L控制蝶形运算的级数

b=1;i=L-1;while(i＞0)

{b=b*2;i--;}//b控制蝶形运算2点之间的距离

for(j=0;j＜=b-1;j++)

{p=1;i=7-L;

while(i＞0)/*p=pow(2,7-L)*j;

{p=p*2;i--;}

p=p*j;//计算旋转因子虚实部在数组中的对应序号p

for(k=j;k＜128;k=k+2*b)//完成本级N/2个蝶形运算

{TR=dataR[k];TI=dataI[k];temp=dataR[k+b];

dataR[k]=dataR[k]+dataR[k+b]*cos_tab[p]+dataI[k+b]*sin_tab[p];

dataI[k]=dataI[k]-dataR[k+b]*sin_tab[p]+dataI[k+b]*cos_tab[p];

dataR[k+b]=TR-dataR[k+b]*cos_tab[p]-dataI[k+b]*sin_tab[p];

dataI[k+b]=TI+temp*sin_ tab[p]-dataI[k+b]*cos_ tab[p];}

}

}

3.2.4 FFT结果的处理[6]

根据采样定理,只要采样频率大于信号频率的2倍,采样得到的数字信号就可以做FFT变换了。N个采样点经过FFT之后就可得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。假设采样频率为fs,信号频率为f,采样点数为N。那么FFT之后结果就是一个为N点的复数,每个点就对应有一个频率点。这个点的模值就是该频率值下的幅度,而每个点的相位就是该频率下的信号的相位。FFT运算后第一个点表示直流分量(即0 Hz),第n个点所表示的频率为:fn=(n-1)*fs/N。

4 实验分析

为了验证程序的正确性,使用手持式振动信号采集系统对FG1617函数波形信号发生器产生的标准9 Hz矩形波进行数据采集,采样频率设为128 Hz(该系统可以在10～1 000 Hz之间灵活设置采样频率)。然后截取采集到的128个连续数据点,使用Lab VIEW编制的专用FFT处理程序和ATmega64L内嵌的FFT程序分别进行分析,得到的幅频结果如表1所示。

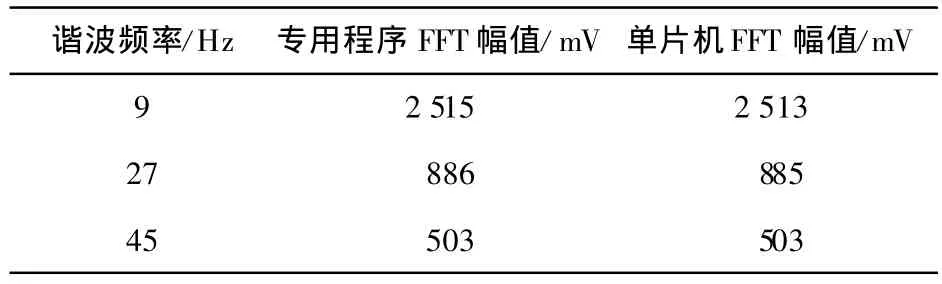
表1 FFT结果比较表

通过比较分析发现,ATmega64L单片机对128点采样数据进行FFT,计算所得到的谐波主频和幅值与使用专用数据处理程序计算得到的主频和幅值基本吻合,达到设计要求精度。

5 结束语

FFT是信号采集领域的重要数据处理工具。上述充分利用高性能低成本的ATmega64L单片机硬件资源和高速运算能力,结合查表手段,可以在220 ms时间内完成128点的32位精度浮点FFT运算,而且经过实验验证转换结果正确、精度够用,证明了该型号单片机实现FFT运算的可行性,为FFT实现方法开辟了新的应用领域。在低成本手持振动信号采集仪器上集成FFT功能,通过对现场采集的振动信号进行实时FFT运算,算出被检测机器的振动主频和幅值,实现了对采样数据的现场分析,满足了设备运行状态检测和故障初判的要求。

[1]肖 飞.手持式振动测试系统的软件开发[D].南京:东南大学,2005:1-5.

[2]贾民平,刘玉春,钟秉林,等.便携式数据采集与工况监测分析系统的研制[J].东南大学学大报,1997,27(2):99-102.

[3]胡广书.数字信号处理—理论、算法与实现[M].北京:清华大学出版社,2003:177-198.

[4]文其林,白晓东,周 洪,等.2048点FFT在TMS320C240x定点DSP上的实现[J].微计算机信息,2006(5-2):159-160.

[5]肖宛昂.嵌人式系统中FFT算法研究[J].单片机与嵌入式系统应用,2003(1):69-71.

[6]李全利,刘长亮.CCS上FFT运算的实现[J].自动化技术____与应用,2009,28(2):61-63.