高速数据传输中的LDPC码译码算法研究

魏瑞刚,陈 晖,邱金蕙,郝志松,雷光雄

(1.中国电子科技集团公司第五十四研究所,河北石家庄050081;2.河北医科大学第三医院,河北石家庄050051)

0 引言

LDPC码是线性分组码中的一种,它具有接近香农限的性能,同时具有更低的线性译码复杂度,而且描述简单,对严格的理论分析具有可验证性,在长码时其性能甚至超过了Turbo码,具有较大的灵活性和较低的差错地板特性。此外,LDPC码译码复杂度低于Turbo码,可实现完全的并行操作,便于硬件实现,吞吐量大,极具高速译码潜力。

1 LDPC码译码算法

LDPC码的校验矩阵H可以用Tanner(泰勒)图表示,校验矩阵H的行与Tanner图中的变量节点有关,校验矩阵 H的列与Tanner图中的校验节点有关,每一个校验节点都有一条或多条线与变量节点相连,这种线被称为边,它代表每一个校验方程中具体参与的信息位,它与奇偶校验矩阵中的“1”是一一对应的。

1.1 LLR-BP算法

1.1.1 初始化

根据接收信号计算变量节点的初始对数域的概率信息L(Pi),i=1,2,…,N,初始化完成后,设定传向与每一个变量节点i相邻的校验节点j(j∈C(i))的对数域的外部概率信息,即

1.1.2 校验节点到变量节点信息更新

校验节点j得到与之相邻的变量节点传来的外部概率信息后进行信息更新,并将更新结果传给所有与校验节点j相邻的变量节点。更新公式为:

式中,l为迭代次数。

1.1.3 变量节点到校验节点信息更新

变量节点i得到与之相邻的校验节点传来的外部概率信息后进行信息更新,并将更新结果传给所有与变量节点i相邻的校验节点。更新公式为:

1.1.4 译码判决

每次迭代译码的最后,进行一次硬判决译码。判决公式为:

若L(l)(qi)＞0则否则

1.2 最小和译码算法

如果对校验节点信息更新处理算法做一近似处理,如式(5)所示,则称为最小和译码算法,最小和译码的其他步骤和LLR-BP算法一样。

1.3 改进最小和算法

如果将最小和译码算法的变量信息前面乘以一修正因子,这样不但能降低校验节点消息处理的复杂度,还能补偿变量节点消息之间的相关性,其更新公式为:

改进最小和译码算法的流程图如图1所示,具体步骤如下:

①初始化。同LLR-BP算法;

②校验节点到变量节点信息更新。同最小和算法;

③变量节点到校验节点信息更新;

④译码判决。同LLR-BP算法。

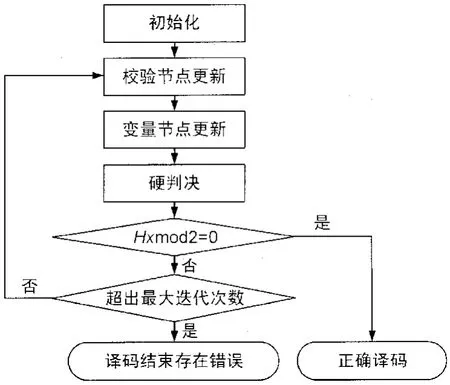
图1 改进最小和译码算法流程

2 算法仿真分析

2.1 译码算法复杂度分析

为了对比LLR-BP算法、最小和算法、改进BP算法的计算复杂度,现选用码率为1/2、码长为8 064 bit的(3,6)LDPC码,得出在各种译码算法下的1次迭代运算量,如表1所示。

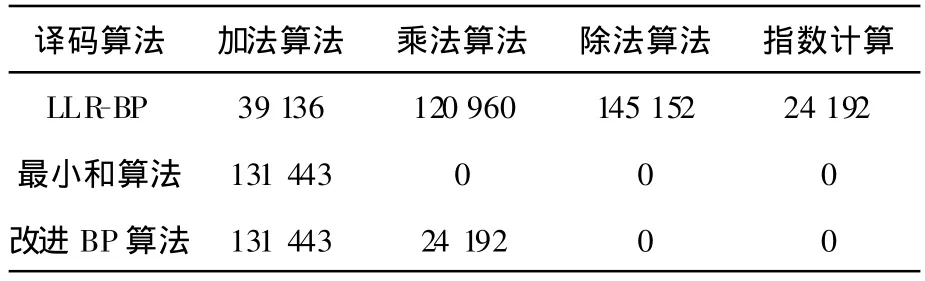
表1 不同译码算法计算量比较

由表1可以看出,8 064 bit的LDPC码在各种译码算法下的1次迭代运算,运算量最小的是最小和算法,改进最小和算法比最小和算法多了24 192次的实数乘法运算,LLR-BP算法的运算量比较大。

2.2 不同修正因子的译码性能分析

为了分析改进译码算法中的修正因子α对译码性能的影响,现选用码长为8 064 bit、码率为1/2的(3,6)LDPC码,仿真得到信噪比分别为0.5 dB、1.0 dB和1.5 dB时,不同修正因子α的译码性能曲线如图2所示。

图2 改进最小和算法修正因子对误码率影响曲线

由图2可以看出在改进型最小和译码算法下,随着信噪比的增加,不同的修正因子对误码率的影响也加大,而且在等信噪比时当α取0.8时,得到的误码率最小,译码性能最好。

2.3 不同算法的译码性能分析

为了对比LLR-BP算法、最小和算法、改进的最小和算法的性能,现选用码长为8 064 bit、码率为1/2的LDPC码采用BPSK调制,在高斯白噪声信道下最大迭代次数为15次时(其中改进最小和译码算法的修正因子取0.8)仿真得到的误码率性能曲线如图3所示。

图3 不同译码算法下的译码性能曲线

由图3可以看出LLR-BP算法、最小和算法、改进型译码算法在高信噪比时均可呈现较低的误码率,其中LLR-BP算法的误码率较好,最小和算法通过简化校验节点信息的处理造成了性能上的损失,改进型译码算法通过修正变量节点的数据可以使性能得到较好的提高。

2.4 不同算法的平均迭代次数分析

现选用码长为8 064 bit、码率为1/2的 LDPC码,最大迭代次数为50,LLR-BP算法、最小和算法、改进的最小和译码算法 3种不同算法误码率在10-7时的平均迭代次数曲线如图4所示(其中改进最小和译码算法的修正因子取0.8)。

图4 不同译码算法下的平均迭代次数曲线

由图4可以看出,LLR-BP算 法、最小和算法、改进型译码算法这3种译码算法的平均迭代次数都随着Eb/N0的增加而下降,且在相同情况下,改进型译码算法的平均迭代次数几乎与LLR-BP算法相同,这表明改进型译码算法相比复杂度较低的最小和算法加快了译码收敛的速度。

2.5 译码吞吐量分析

为了分析改进译码算法的译码吞吐量,现将该译码算法应用在时钟为150 MHz的某高速系统中,在该系统中选用码长为8 064 bit,码率为7/8的准循环LDPC码,译码器采用并行交迭的译码结构,在该结构中变量信息迭代和校验信息迭代共需要336*2=672个时钟周期,再加上延迟保护的24个时钟,所以每次迭代需要672+24=696个时钟周期。由上述分析可知,选用15次迭代就可以达到系统所需的误码率要求,故共需要15*696=10 440个时钟周期,再加入初始化所需的时钟周期,最终译码共需要11 448个时钟周期。因此吞吐量可达到8 064*7/8*150*2/11 448=184.906 Mbps。

3 结束语

改进的译码算法一方面由于校验消息的处理简化为只有加法运算,同时对变量消息进行乘性校正,故总的运算量要低于LLR-BP算法,译码性能要高于最小和算法,这在译码性能和计算复杂度之间达到了较好的折中;另一方面改进的译码算法在相同的误码率的情况下译码的平均迭代次数略低于LLR-BP算法,这改善了算法的收敛特性,降低了译码延迟。因此改进的译码算法不但较好地降低了译码复杂度,而且依然可以得到高吞吐量,这在高速译码中具有广泛的应用前景。

[1]GALLAGER R G.Low-Density Parity-Check Codes[M].Cambridge,MA:MIT Press,1963.

[2]钟 州,李云洲.基于LDPC码校验节点度的分类修正最小和算法[J].清华大学学报(自然科学版),2009,49(1):45-48.

[3]张靖琳,刘荣科,赵 岭.高码率LDPC码译码器的优化设计与实现[J].电子与信息学报,2009,31(1):83-86.

[4]LI Z W,VIJAYA KUMAR B V K.A Class of Good Quasicyclic Low-density Parity Check Codes Based on Progressive Edge Growth Graph[C]//Signals,Systems and Computers Conference Record of the Thirty-Eighth Asi-lomar Conference on,2004:1990-1994.

[5]FOSSORIERM,MIHALJEVIC M,LMAIH.Reduced Complexity Iterative Decoding of Low Density Parity Check Codes Based on Belief Propagation[C].IEEE Transactions on Communications,1999:673-680.

[6]张金贵,斐文端,许星辰.一种提高LDPC译码器吞吐率的译码算法[J].无线电工程,2008,38(6):49-52.