基于定向天线的导航信号参数估计方法研究

罗显志

(1.河北省卫星导航技术与装备工程技术研究中心,河北石家庄050081;2.中国电子科技集团第五十四研究所,河北石家庄050081)

0 引言

虽然各国都根据自己的实际需求设计出了不同调制方式的导航信号,但BPSK和BOC调制是目前所有导航系统中使用最广泛的2种调制方式。下面主要研究非合作BPSK调制信号和非合作BOC调制信号的多普勒、码速率、码周期、信号功率和码序列的检测和估计问题。为了实现对以上非合作导航信号的检测和估计,这里使用循环谱统计量[1-4]方法实现了对信号多普勒、码速率和信号功率的估计,并提出了基于自相关的码周期估计算法和基于滑动相关的码序列估计方法。

1 监测系统结构和参数估计步骤

GNSS信号监测系统包括定向天线(含馈源)、带通滤波器、低噪声放大器、矢量信号分析仪和伺服等组成,体系结构如图1所示。该系统能够接收所有L频段的GNSS信号(频率范围为1.1～1.7GHz),定向天线的波束宽度要尽可能窄,增益要足够大,以满足后序信号处理信噪比要求;卫星跟踪软件根据卫星星历预测卫星位置和速度,并通过天线伺服系统控制定向天线的指向被跟踪卫星。

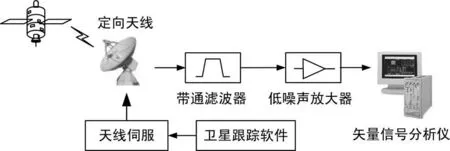
图1 GNSS信号监测系统体系结构

根据国际电联发布的卫星信号参数(中心频率、带宽、信号强度)设置矢量信号分析仪的中心频率、采样速率和信号动态范围。矢量信号分析仪实现信号的下变频、抽取和滤波操作,并存储一定长度的数据。在信号检测和参数估计过程中,首先采用循环谱估计方法估计多普勒频率和码速率,用估计的多普勒修正采集的数据,实现多普勒剥离,然后采用自相关运算估计信号码周期,采用滑动相关方法剥离电文,最后将同相位码数据进行叠加,估计测距码的码结构和码相位。

2 GNSS信号检测与参数估计算法

2.1 基于循环谱的多普勒/码速率/信号功率估计

假设基带导航信号为BPSK信号,则其实部可以表示为:

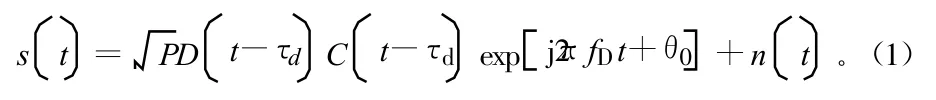
根据谱相关理论,可得基带BPSK信号的循环谱[1,2](不考虑噪声影响):

式中,fD为残存的多普勒频移;α为循环频率;Tc为码元时宽由式(2)可知,BPSK有多个循环频率,且循环谱与信号相位编码方式无关,与载频、码元速率、初时时间和初始相位有关。当f=0时,BPSK信号的循环谱包络为:

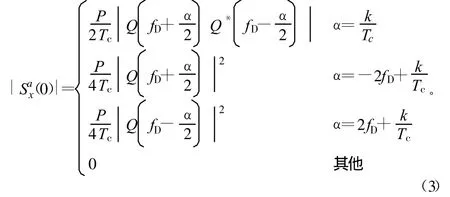
由式(3)可见,该包络仅与信号载频、码元时宽和幅度有关,与信号初始时间和初相无关。不难看出等式右边除第2项有较大的非零值外,其他都为零或接近零的小值,其中最大峰值出现在循环频率α=±2fD处,故在频谱为零的循环谱相关密度函数包络的非零循环频率上搜索最大峰,并确定其位置,可估计出载频。此外,可以看出的次最大峰出现在循环频率处,与最大峰的间隔恰好为码速率,即为码片时宽的倒数,故搜索次最大峰并确定与最大峰的间隔,可估计直接序列扩展频谱信号的码速率。而循环频率 α=±2fD处的峰值与信号功率成正比,与伪码码速率成反比。另外需要说明的是,BOC调制信号的副载波导致单个码片时间内出现多个方波调制的副载波,式(3)的Tc应理解为副载波切片的长度。

综上述可得GNSS信号多普勒(载频)、码速率(码宽)和信号功率估计器的表达式为:

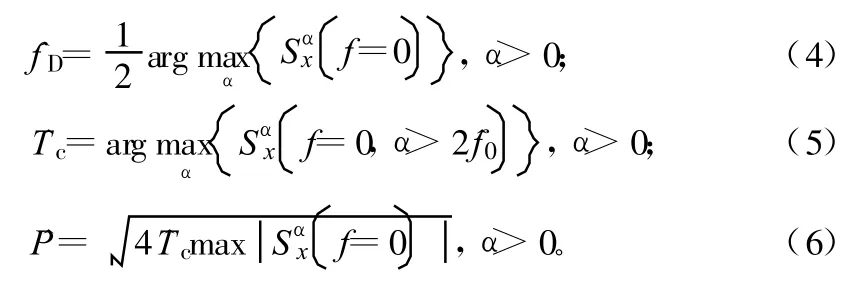
2.2 基于自相关的码周期估计

式(1)所示的基带信号自相关函数为(不考虑噪声的影响):

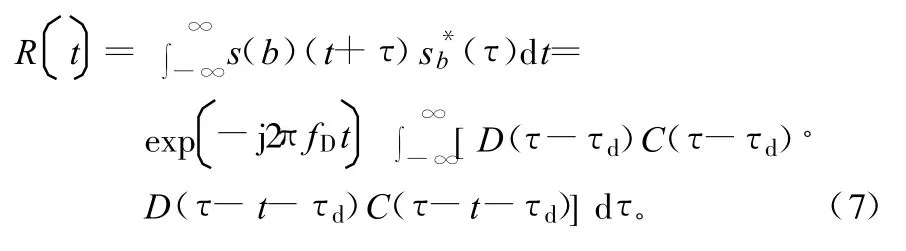
而其模为:

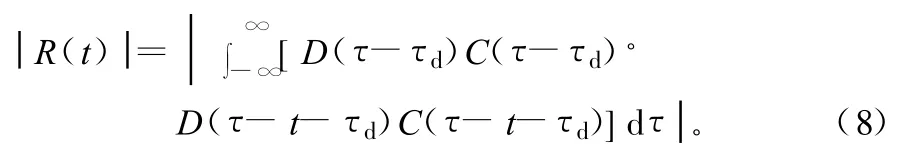
由式(8)可知,基带信号自相关函数的模可以表示为数据调制的伪码序列的滑动相关,多普勒频移对相关结果没有影响,而由于伪码存在周期性,基带自相关函数的模在码周期重叠部位会出现峰值。所以,式(8)可以用来估计码周期。

2.3 基于滑动相关和数据累加的码相位估计

完成码周期估计后,从基带信号中取出小于码周期长度的一小段数据,该切片数据可以表示为:

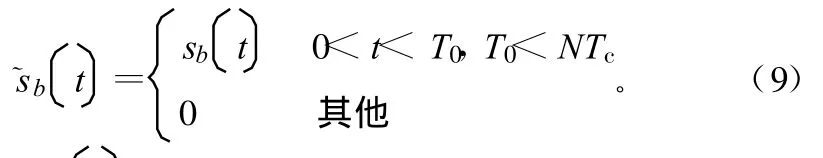
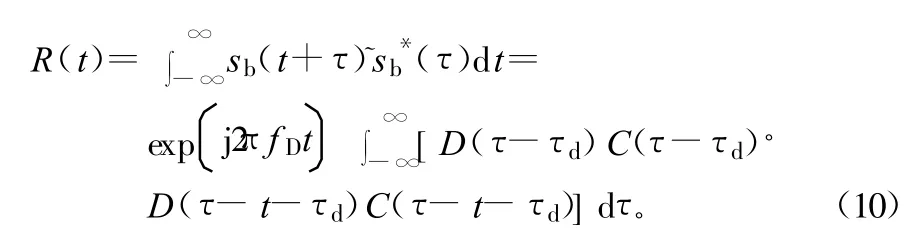
基带信号与其自身切片信号的滑动相关示意图如图2所示,当切片数据与原始数据的码对齐时,滑动相关函数将出现峰值,即

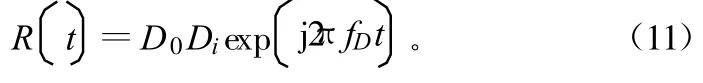
当fD=0时,式(16)可以用来判别数据为D0的极性。然后根据Di的极性按周期翻转原始基带数据,如图2所示。所以内的数据是以Td为周期的切片长度为T0的伪码信号,将所有这些数据叠加就能提高基带信号的信噪比,从而可获得原始样本数据的码相位,即

获得τd后,将原始数据延迟 τd再按以上方法就可求解调制在样本数据上的码序列。

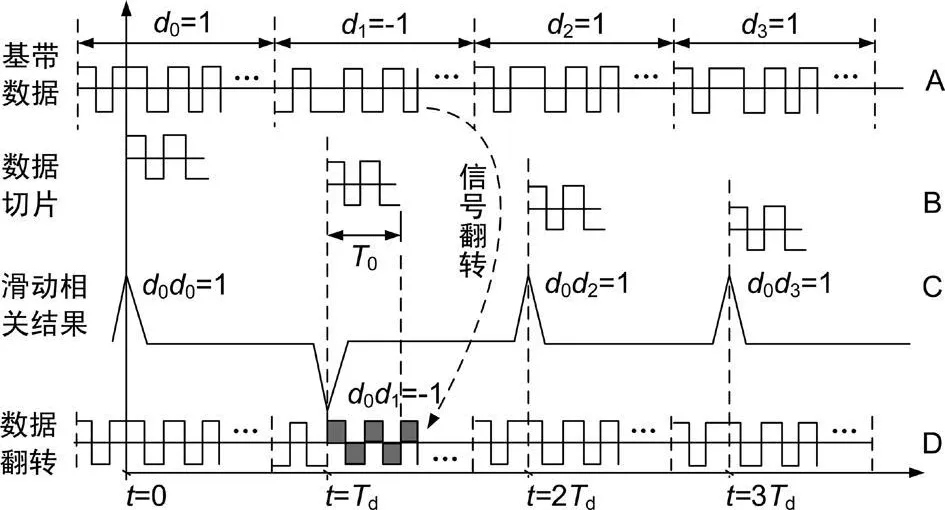
图2 基带信号滑动相关及数据翻转

3 仿真与验证

下面通过计算机仿真实验进一步验证以上分析的结果。仿真中的输入信号假设为一个BPSK-R(1)信号,码速率为 1.023 MHz,码周期为1 ms,信号幅度假设为单位1,信号采样率为5 MHz。信噪比为0 dB时BPSK-R(1)信号的循环谱和f=0 MHz时循环谱 α截面图如图 3所示。由图可知,在 α=±2.5 MHz处出现峰值,在 α=±2.5∓1/TdMHz处出现次峰值。为了加快运算速度,以上所有循环谱的计算都使用了基于FFT累加快速算法[5]。

综上所述,循环谱方法能够正确估计GNSS信号的功率、载频(多普勒)和码速率。

BPSK-R(1)基带信号自相关函数如图4所示,多普勒频率为4 Hz,信号采样率为5 MHz。显然,图中的相关峰每5000个采样点出现1次,对应的码周期为1 ms。

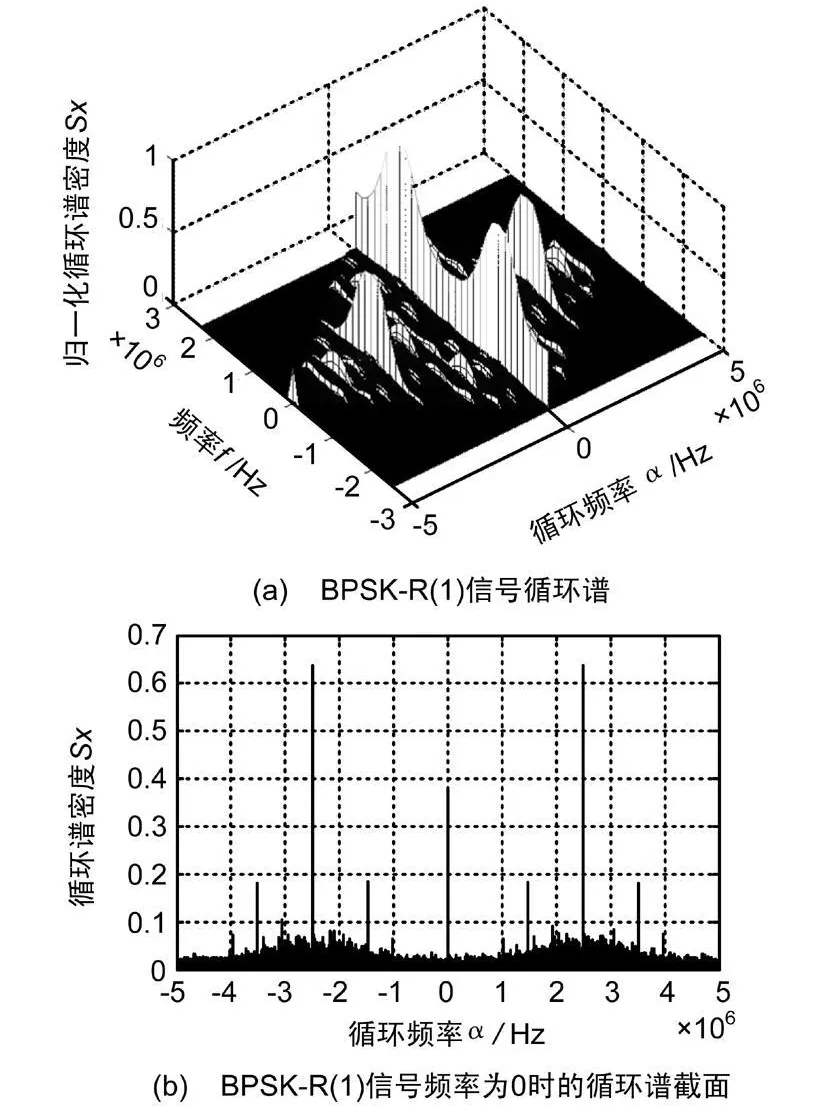
图3 BPSK-R(1)信号循环谱和循环谱α截面

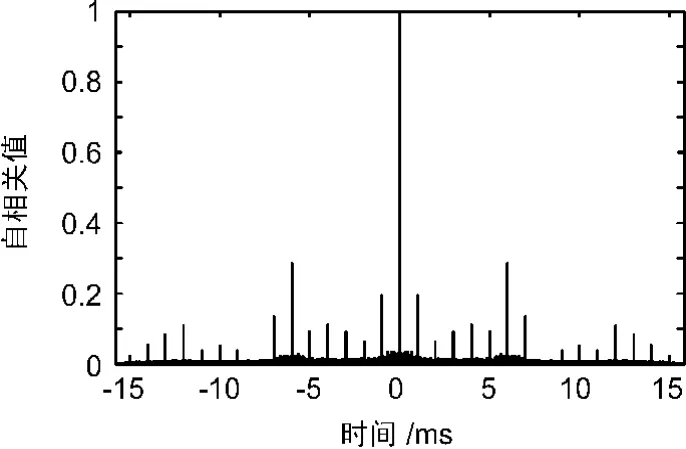
图4 BPSK-R(1)基带信号自相关

BPSK-R(1)基带信号的滑动相关函数如图5所示,多普勒频率为4 Hz,信号采样率为5 MHz。显然,由于多普勒频率的影响,信号出现包络特性。多普勒消除后的BPSK-R(1)基带信号的滑动相关函数如图6所示,信号采样率为5 MHz。显然,消除多普勒频率后的滑动相关函数峰值基本相等,不再存在正弦包络特性,但相关峰依然保留数据调制后的正负特性。消除多普勒并剥离数据后100个码周期累加后的基带数据如图7所示。在起始位置4 000点左右出现幅度包络的阶越特性,这主要是由于数据剥离过程中相位翻转导致的,由此可以推断出码相位为0.8 ms左右。估计出的码序列与原始信号码序列如图8所示,显然,估计出的码序列除极性相反外,码序列完全相同。

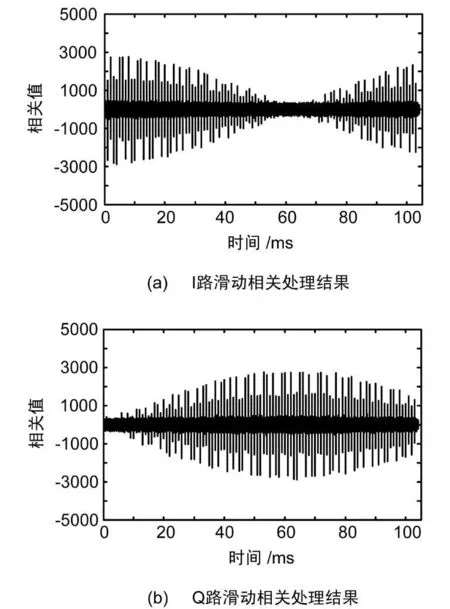
图5 基带信号(含多普勒)滑动相关处理结果

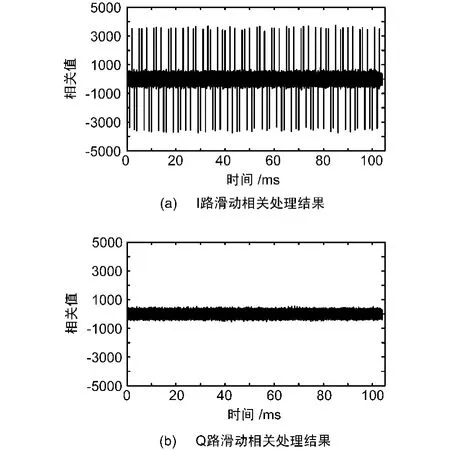
图6 多普勒消除后基带信号滑动相关处理结果

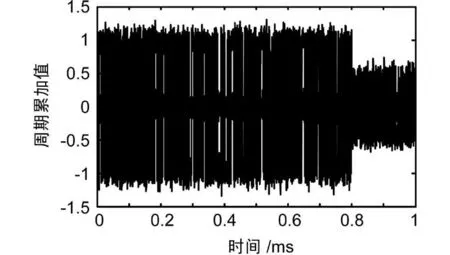
图7 100个滑动相关码周期累加后的基带数据

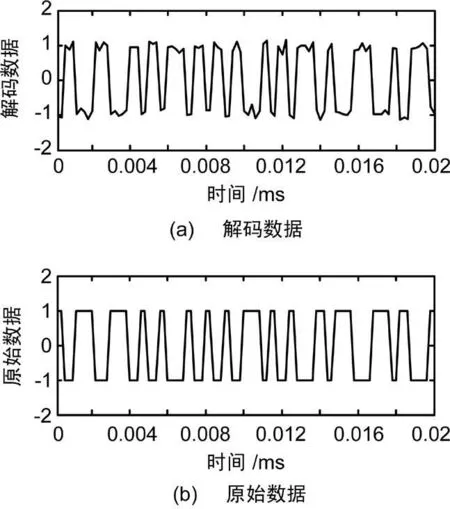
图8 原始信号码序列和估计的码序列

4 结束语

上述以非合作导航信号监测为背景,提出一套切实有效的方法实现了低信噪比条件下非合作导航信号的盲检测和载波频率、码速率、码周期、信号功率和测距码码序列的盲估计。通过仿真验证了所提出方法的有效性。

[1]GARDNER W A.Spectral Correlation of Modulated Signals:Part 1-Analog Modulation[J].IEEE Trans Commun,1987,COM-35(6):584-594.

[2]GARDNER W A.Spectral Correlation of Modulated Signals:Part 2-Digital modulation[J].IEEE Trans Commun,1987,COM-35(6):595-601.

[3]黄春琳,柳 征,姜文利,等.基于循环谱包络的扩谱直序信号的码片时宽、载频、幅度估计[J].电子学报,2002,30(9):1353-1356.

[4]VADURSI M.A New Instrument Based on Cyclic Spectral Analysis for Power Measurement in Digital Telecommunication Systems[C].IEEE Instrumentation and Measurement Technology Conference Proceedings,2008:1-6.

[5]ROBERTSRS,BR OWNWA,LOOMISHHJR.Computationally EfficientAlgorithms forCyclic Spectral Analysis[J].IEEE Signal Processing Mug.,1991,8(2).38-49.