受电弓试验台垂向激振系统设计

胡继胜，关吉瑞，冯庆胜

(1.大连交通大学 交通运输工程学院，辽宁 大连 116028;2.大连交通大学 电气信息学院，辽宁 大连116028)

0 引言

受电弓靠滑动接触而受流，是车辆与固定供电装置之间的连接环节，其性能优劣直接影响电动车辆工作的可靠性［1］.为准确地评价受电弓性能，需要建立一套能模拟受电弓实际运行状态的综合性能试验系统，该系统应具有模拟弓网间纵向运动、弓网间垂向振动、弓网间之字形运动和受电弓底座垂向振动的功能.由于受电弓底座直接安装在电动车辆顶部，车辆在运行过程中的任何振动将通过车顶直接传递给受电弓，进而影响弓网动态相互作用.当轨道存在几何不平顺时，车辆与轨道的耦合振动增强，而在中高速运行条件下，这种耦合振动则更为剧烈.相应地，由车顶传至弓网系统的振动干扰也将加大［2］.这些振动是影响受电弓工作性能的重要因素，因此受电弓综合性能试验系统应能对受电弓底座垂向振动进行模拟，采用的激振系统能模拟出车辆运行时受电弓底座在不同运行状态下的振动工况.

在综合性能试验系统中，受电弓作为被试设备具有较大的质量，因此垂向激振系统振动部分的质量也较大，同时该激振系统还具有系统工作频带较窄(0.5～3 Hz)，振动幅值较大(0～0.02 m)，并要求频率、幅值连续可调的特点.在激振设计时没有采用传统的结构复杂、成本较高的通用振动试验系统的设计思路，而是采用伺服电动机和旋转—直线位移转换装置组成的激振器作为本振动系统的激振装置，这样在满足系统要求的同时，使结构简化，成本大为降低，实现了对受电弓底座垂向振动幅值、频率的连续控制，使得系统能够以较低成本可靠低运行.

1 受电弓试验台垂向激振系统的原理及结构设计

本文设计的受电弓垂向激振系统的结构如图1所示，主要由受电弓振动平台、伺服电机与旋转—直线位移转换装置构成的激振器、主振弹簧、导柱和底座等组成，受电弓与振动平台连成一体同步运动.

伺服电机安装在底座上，在伺服电机的轴端安装有转盘，钢索固定在转盘上，而另一端与受电弓振动平台相连.在受电弓振动平台与底座之间还对称的安装了四根导柱，四根主振弹簧分别套在导柱上.导柱不仅在受电弓振动平台振动过程中起到导向的作用;同时作为主振弹簧的导杆，在弹簧轴向载荷过大而失稳时，可以起到保护作用.受电弓垂向激振系统是通过控制伺服电机转轴按一定幅度、频率连续摆动，并在弹簧及旋转—直线位移转换装置的作用下，将电机转轴的摆动转换为振动平台的振动.通过对伺服电机摆动角度幅值及频率的控制即可实现对振动平台振动幅值、频率的控制.

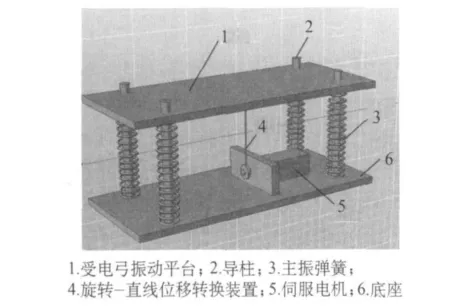
图1 受电弓垂向激振系统三维图

2 激振系统动力学分析及参数的确定

2.1 激振系统动力学分析

根据图1所示的受电弓垂向激振系统可建立其动力学模型，如图2所示.

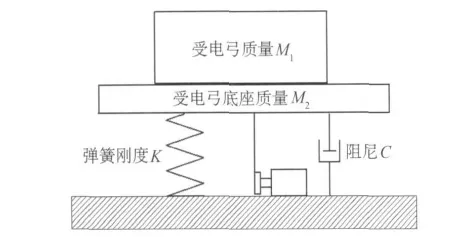
图2 受电弓垂向激振系统动力学模型

从此模型可以看出整个振动系统受到的是非简谐激振力，并且此激振力是周期性变化的.但在设计中，将振动系统看作是简谐激励作用下的系统，由此可以列出动力学方程:

强迫振动的振幅为:

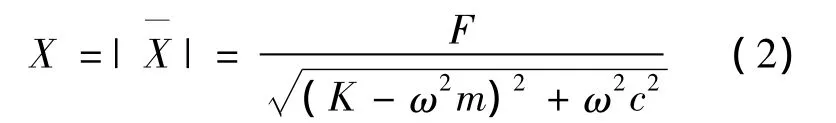
稳态时的激振力为:

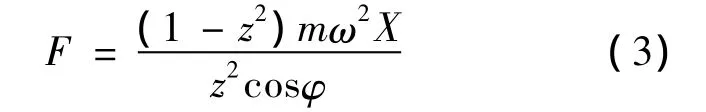
式中，m为振动部分的质量，kg;φ为相位差角;ω为强迫振动圆频率，ω =2πf，f为振动频率;z为振动频率比为振动系统的固有频率=ω0;K为激振弹簧的刚度，N/m.

由于近亚共振频率点工作的振动系统在稳态振动时所需的激振力较小，并且激振力与振动方向同向，因此本振动系统工作在近亚共振频率点附近［3］.

本激振系统振动部分的质量包括受电弓质量M1与受电弓底座质量M2，合计203 kg，振动幅值设定为0.02 m，频率设定为3 Hz.

2.2 主振弹簧的参数选择

本试验台的受电弓垂向振动系统的频率比选择在0.95，在强迫振动频率最大为3 Hz的情况下，可计算出系统的固有频率ω0=19.84 rad/s.主振弹簧的刚度按式(4)确定:

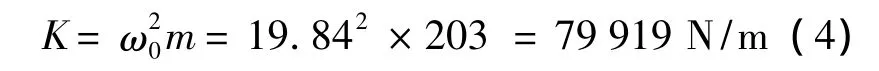
由于弹簧系统采用4个弹簧并联的结构形式，因此，单个弹簧的刚度为K=19 980 N/m.

2.3 伺服电机的选型

伺服电机的选取应以满足系统动态特性为前提，在选取时，应充分考虑振动物体的当量转动惯量及振动频率的要求:

(1)伺服电机转动惯量的确定

本系统通过伺服电机对受电弓平台振动的幅值、频率进行连续控制，伺服电机应具有良好的动态特性.在伺服系统设计中，通常依据负载惯量的计算结果预选使用的伺服电机规格.选用原则是伺服电机转动惯量大于负载惯量的1/10，以确保本系统具有良好的动态特性［4］.之所以选用转动惯量较大的伺服电机，原因是伺服系统运动定位频率较高时需要较短的加速时间来配合，而转动惯量较大的伺服电机通常有较大的输出转矩，可更快地加速，使得伺服系统具有较好的随动特性.

式中，JL为伺服电机转轴换算负载惯量(kg·cm2);M为负载的当量质量(kg);D为电机轴的直径(cm)，已知为5 cm.

在本系统中，伺服电机拉动负载的力F为:

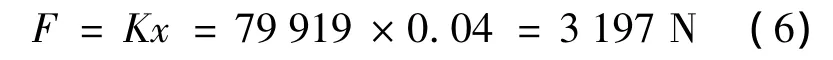
则 M=319.70 kg.

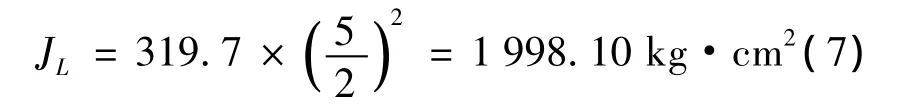
本试验台选用的是北京首科凯奇的186NYSL212型伺服电机，其转动惯量为214 kg·cm2，最大转矩为175 N·m，额定转矩为55.6 N·m，电机转动惯量约为负载惯量的1/10.

(2)伺服电机负载转矩的确定

伺服电机的负载转矩按照伺服电机驱动弹簧在平衡位置时压缩0.04 m所施加的力来计算:

(3)伺服电机加速转矩的确定

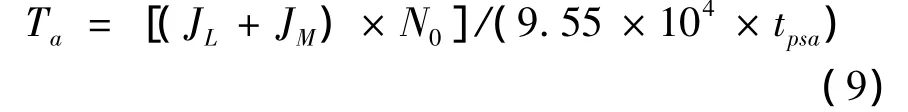
式中，负载惯量为 JL=1 998.10 kg·cm2，电机惯量为214 kg·cm2，电机转速为 N0=144 r/min，加速度时间为tpsa=1/12 s，则:

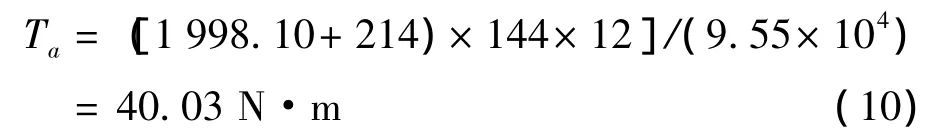
伺服电机的转动惯量、负载转矩及加速转矩应能满足以上的要求，本系统选用的186NYSL212型伺服电机的最大转矩为175 N·m，上述参数中，加速转矩 Ta与负载转矩 TL之和为119.96 N·m，其值小于最大转矩175 N·m，因此所选伺服电机满足要求.

3 激振系统的控制策略及程序设计

3.1 激振装置控制与驱动系统

本受电弓垂向激振系统采用伺服电机及旋转—直线位移转换装置作为激振器，该激振装置的控制及驱动系统由工业控制机、PCI-6229多功能数据采集卡和CSD-DH-30型伺服电机驱动器组成.工业控制机通过PCI-6229的D/A转换器输出端口，经低通滤波器向伺服电机驱动器输送转速拟控制信号，此模拟量信号的范围是－10～+10 V，对应于伺服电机的速度为－1 440～+1 440 r/min.因此伺服电机转速模拟控制信号作为速度指令可以控制伺服电机的工作状态，从而实现对伺服电机摆动幅度、频率的连续控制，进而实现对振动平台振幅、频率的连续控制.

3.2 振动控制策略的确定

本振动系统利用旋转—直线位移转换装置给振动平台施加激振力，但如果以静态时弹簧被压缩后的平衡位置为零位控制伺服电机摆动，由能量守恒定理可知，在频率较低(与振动系统固有频率相比)的情况下，振动幅值将远低于预设的振动幅值.

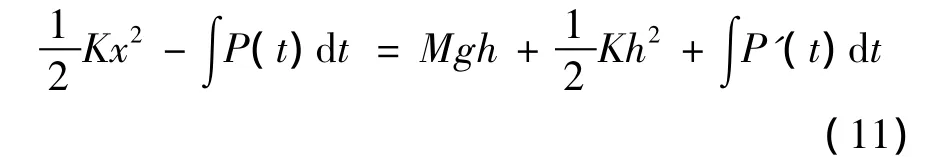
式中，P(t)为上升阶段，电机驱动钢索阻碍负载上升所做的功;P'(t)为负载过平衡位置后，电机驱动钢索阻碍负载上升所做的功;h为负载过平衡位置后上升的高度.

负载过平衡位置后上升的高度为:

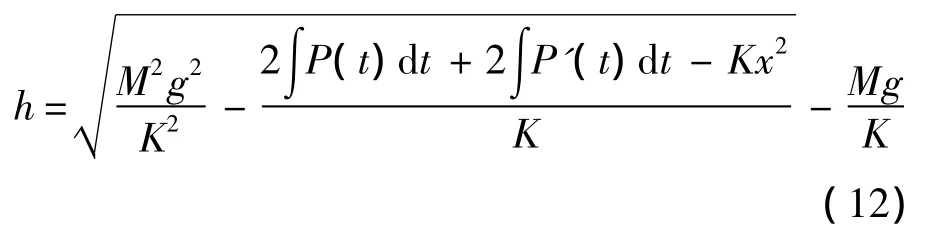
当振动频率低于系统固有频率的前提下，受电弓振动平台向上运动时，由于弹簧受到伺服电机摆动速度的限制，弹簧所储能量一部分用于克服伺服电机对振动平台上升产生的阻力.因此频率越低，弹簧过平衡位置后继续上升的高度就越低.

可见，若要达到预想的振动效果，振动时零位必须位于振动平台平衡位置之下，即振动平台应围绕其静态平衡位置之下的某一位置振动，如图3所示.具体的控制方法如下:

将受电弓安装于振动平台之上，整个弹簧系统处于平衡状态时，控制伺服电机旋转，旋转—直线位移转换装置拉动振动平台向下运动，振动平台一旦达到预定的振动零位后，对应的光电行程开关输出平台到达零位的脉冲信号，控制系统控制伺服电机摆动，从而使平台围绕零位振动.

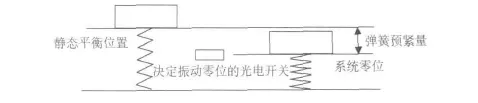
图3 加入光电行程开关后的系统

由于本系统固有频率是按照3 Hz设计的，因此在0.5～3 Hz的频带内，主振弹簧的作用可以保证振动系统的振动速度与伺服电机的摆动速度是对应的.对本试验系统，我们还希望振动系统能够以正弦规律运动，那么就必须对伺服电机的摆动按正弦规律进行控制.

假设振动系统已经按正弦规律在振动，那么其速度同样也是一个正弦规律变化的量，其表达式为:

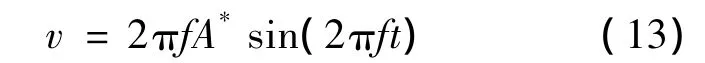
理论上，此速度表达式与伺服电机的摆动速度相对应.利用这样的关系，对伺服电机施加按式(13)关系变化的转速控制电压，伺服电机便按此电压变化规律对应的速度变化规律摆动.

伺服控制系统转速控制电压按以下方法确定:

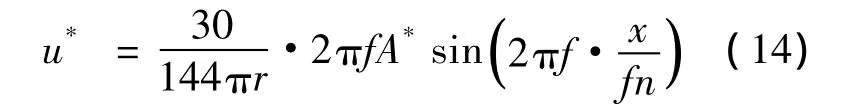
式中，x为程序的循环次数.

在每个采样点处，按u*变化规律确定控制电压，此电压经低通滤波后输出给伺服驱动器，伺服驱动器即可控制伺服电机按照预期规律进行摆动，进而通过旋转—直线位移转换装置驱动受电弓平台振动.

利用以上方法可以控制振动系统的振动频率，尽管伺服电机动态响应较快，但伺服电机系统作为一个惯性环节，速度的变化不可能完全跟随控制电压的变化规律，因此振动幅值控制则需要引入闭环控制.幅值闭环控制方法如图4所示:

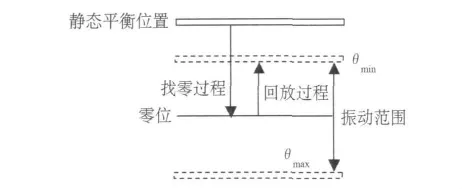
图4 正弦模拟量控制下的运动过程

(1)在振动系统开始工作时，控制伺服电机以低速旋转，振动平台自静态平衡位置下移，系统接受到光电行程开关发出的零位信号，即可确定振动系统的工作零位.

(2)当振动系统寻找到零位后，控制振动平台上行，达到要求的振幅A时，采集此刻伺服电机的角度θmin，以此确定平台振幅，令A*=A并按式(14)确定伺服电机驱动器转速控制电压.进而控制伺服电机以零位为中心作正弦规律变化的摆动，振动系统也随之按正弦规律振动.

(3)在振动平台下行过程中，当振动系统的速度再次为零时，采集此时的伺服电机位置θmax，如与振幅要求不符，则必须调整正弦模拟电压信号的幅值2πfA*，在频率一定时按PI调节规律调整A*值的大小就能实现对振幅的修正，确保平台按设定的振幅振动.同时在控制过程中，每隔数个周期便接收一次光电行程开关所放出的零位开关量信号，这样做的目的是为了消除伺服电机转轴在旋转过程中所产生的位置漂移.

3.3 受电弓垂向激振系统控制程序设计

按计算机控制理论，对于具有惯性规律的受控对象，计算机控制的采样频率在满足fs≥10fmax时，其控制效果基本与模拟控制等价［4］.在编写本垂向激振系统的程序时，将振动周期的时间分为50份，那么每一份所分配的时间为，控制程序每完成一次循环，亦即fs=50fmax，这满足控制过程对采样频率的要求.本激振系统的振动频率最高为3 Hz，要求控制程序在7 ms内必须完成所有的控制算法并产生输出信号.对于微机控制的激振系统而言，控制算法无繁杂计算，系统可轻易地在一个Ts(Ts≥7 ms)内完成所有算法.由于多功能DAQ设备上的模拟输入、模拟输出、数字I/O和计数器功能可同时运行［6］，因此，可以选择图形化编程软件LabVIEW编写振动实时控制程序.分别用DAQmx Create Channel(DI－Digital Input).vi、DAQmx Create Channel(CI－ Position －Angular Encoder).vi、DAQmx Create Channel(AO －Voltage－Basic).vi等控件驱动PCI-6229的各类端口，进而分别通过DAQmx Read(Digital Bool 1Line 1Point).vi、DAQmx Read(Counter DBL 1Chan 1Samp).vi控件对光电行程开关信号和伺服电机编码器的位置信号进行采集.并依据采集到的数据按以上控制策略确定转速控制电压u*，利用 DAQmx Write(Analog DBL 1Chan 1Samp).vi控件通过D/A转换器经低通滤波器将控制电压输出给伺服电机驱动器，进而实时控制伺服电机的摆动.

4 试验结果

为检验本文提出的方法，对受电弓垂向激振系统进行了振动幅值为0.005～0.02 m，振动频率为0.5～3 Hz之间多工况的试验.在实验时，对振动平台的加速度、伺服电机的控制电压以及振动平台位移进行了采集.

以振动幅值为0.01 m，振动频率1、2、3 Hz这三种工况的试验结果说明本系统的运行特性.实验结果如图5～7所示:

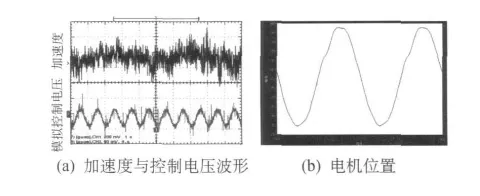
图5 频率1 Hz时的试验特性

图6 频率2 Hz时的试验特性

图7 频率3 Hz时的试验特性

通过实验表明，本激振系统及控制方法能满足受模拟电弓垂向振动的要求.

5 结论

本文提出的受电弓垂向激振系统采用伺服电机与旋转—直线位移转换装置组成的激振器在微机伺服控制系统驱动下，按照这一方法进行控制时，可以满足受电弓垂向振动试验对激振系统的要求，可以确保振动幅值和频率分别在0～0.02 m、0.5～3 Hz之间连续可调.提出的激振方式及其控制方法应用于质量较大的激振系统时与传统的振动试验系统相比，可以较准确地以较低的成本实现对振动频率、幅值的连续调节.

［1］翟婉明，蔡成标.机车—轨道耦合振动对受电弓—接触网系统动力学的影响［J］.铁道学报，1998，20(1):32-38.

［2］闻邦椿，刘树英，何勍.振动机械的理论与动态设计方法［M］.北京:机械工程出版社，2001:98-99.

［3］颜嘉男.伺服电机应用技术［M］.北京:科学出版社，2001:175-177.

［4］何克忠.计算机控制系统分析与设计［M］.北京:清华大学出版社，1990:141-142.

［5］宋雷鸣.动车组传动与控制［M］.北京:中国铁道出版社，2007:256-257.

［6］龙华伟.LabView8.2.1与 DAQ 数据采集［M］.北京:清华大学出版社，2008:257-258.