基于FEM的重型汽车提升桥壳结构强度的分析
2011-06-11于东娜魏建飞邱阳刘学杰
于东娜,魏建飞,邱阳,刘学杰
(1.内蒙古科技大学 机械工程学院,内蒙古 包头 014010;2.包头北奔重汽车桥有限公司,内蒙古 包头014030)
0 引言
随着现代重型汽车行业领域高速发展,对其作业能力的要求越来越高,传统的桥壳设计计算方法就无法满足现代实际情况.任卫群等[1]较系统地探讨了通过计算机模拟仿真技术可以有效地预测桥壳易疲劳受损部位的应力与变形.唐述斌等[2]较早地对后桥壳轻量化进行了有限元分析,明确了对桥壳的研究方向.朱帅等[3]应用ANSYS分析软件对前桥强度进行了详细的仿真分析.而到目前为止,有关对重型汽车提升桥的强度、刚度的校核以及疲劳性测试等理论与实验的研究是整个重型汽车行业迫切需要解决的问题.
本文考察在整车满载或超载下落时提升桥的强度和刚度.此时提升桥的受力形式与非断开式前桥的受力形式相似,桥壳在不同工况下的受力较复杂,主要承受的力分别为越过不平路面时承受最大垂向力、紧急制动时承受的最大制动力和侧滑极限时承受的最大侧向力,这三种典型受力形式易造成提升桥壳结构破坏[4].合理地设计提升桥壳,使其有效地配合整车,提高整车的通过性和平顺性.因此车桥的强度和刚度以及疲劳可靠性是重型汽车设计及制造所必须考虑的重要问题[5],而采用有限元分析技术则是一种行之有效的方法.
1 有限元建模与仿真分析
本文在ANSYS分析软件里直接创建计算模型,保证与实际几何模型尺寸一致的同时,可以忽略不影响分析结果的板簧座、制动盘等实体,使建模工作适当简化.为方便简化计算,在进行有限元分析时做下面两点假设:①板壳与板壳之间,半轴套筒与提升桥壳之间均是一体的,不是装配的,即不考虑焊接、接触分析;②提升桥壳结构材料为一种均质同性材料.
基于该提升桥壳结构静态特性分析的特点,选取SOLID95号三维实体单元.本文中研究的提升桥壳材料为均质的40MnB,其弹性模量为E=2.09e5MPa,泊松比μ =0.28,质量密度ρ=7.93 kg/mm3,屈服极限σs=785MPa,强度极限σb=980MPa,弯曲强度σc=490 MPa.由于该材料为塑性材料,则以屈服强度为基准作为极限应力.本文中取强度安全系数 n=1.5,那么许用应力值[σ] =σs/n=523 MPa.
1.1 模型建立
在实体建模时,采用自下而上方法来建模,即先建立关键点,连接关键点生成线,连接线生成面,最后生成体的顺序[6].应用ANSYS分析软件来直接创建三维实体具体步骤如下:
(1)在ANSYS默认的当前笛卡尔XY平面坐标系下,创建提升桥壳方形壳处的一个平面,四个顶角处做倒角处理;
(2)在该方环形平面中心点处沿Z轴创建一条中央轴线,采用面沿中央轴线来挤出方形壳体;
(3)在该桥壳的方形壳体右侧即Z轴的负方向,创建使方形壳体过渡到圆形壳体处的等厚壁收口壳体;
(4)按照实际模型尺寸来构建半轴套筒,采用映射方法使得在桥壳的方形壳体左侧即Z轴的正方自动生成等厚壁收口壳体与半轴套筒;
(5)删除在创建过程中的辅助或多于的点、线、面,最后进行布尔操作,该提升桥壳体三维实体模型创建完成.
在提升桥两侧上板簧座和下板簧座所在位置处设置独立的计算面积区域,载荷与约束就直接施加此处,既有利于模型的简化,提高计算速度;又可以方便观察载荷计算后应力分布情况.完成的提升桥壳三维实体模型如图1所示.
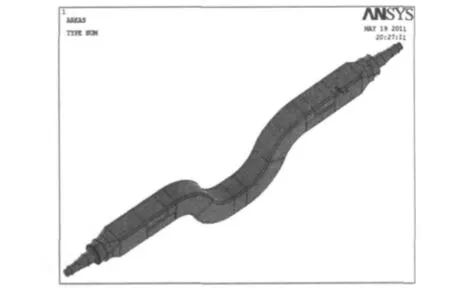
图1 提升桥壳三维实体模型
1.2 网格划分
该提升桥壳是由方形壳体与实心圆轴体相结合的,即存在过渡梯形区域,采用自由网格划分会减轻在前处理过程中的工作量,效率提高.针对三种典型工况下分析提升桥壳的静态强度特性,则模型的网格尺寸及其他单元特性必须遵循一致性原则.由于在最大制动力工况下,需要对空气弹簧座外侧与制动盘所在位置的半轴套筒之间的壳体施加转矩[7],为了确保计算的精确性,我们采用节点耦合的办法,这就需要在所要施加转矩位置正中央创建2个节点,在该节点上创建2个MASS质量单元,设置实常数并应用CERIG命令来建立刚性区域使其节点耦合.其它两种工况则直接采用原始网格单元模型,智能网格尺寸控制在5较为适宜,得到168 821个单元,283 125个节点.生成的原始提升桥壳有限元模型如图2所示.

图2 提升桥壳有限元模型
1.3 仿真分析
提升桥壳在三种典型工况下进行的静态特性分析所需要的参数为:提升桥壳自重m1为400 kg;提升桥满载载荷m2为7 500 kg;提升桥车轮轮距B1为2.372 m;两空气弹簧座中心间距离 B2为1.2 m;车轮滚动半径 rr为0.545 m;动载系数 kv为2.5;整车制动时质量转移系数m'为0.8;道路附着系数 φ 为0.68;侧滑系数 φ'为1.0.
由于提升桥壳自重远小于满载载荷,所以计算桥壳受力分析不考虑自重的影响,只需为最大制动力工况下有限元模型中的MASS21质量单元设置实常数MASS.
1.3.1 提升桥壳的受力分析
(1)工况一:越过不平路面时桥壳承受的最大垂向力
整车在满载越过不平路面时,只受到唯一垂向冲击载荷的作用下,最大垂向力取满载载荷时的2.5倍.此时提升桥壳相当于一个简支梁,桥壳通过半轴套筒轴承支撑在轮毂上,半轴套筒的支撑点位于车轮的中心线上[2],即车轮轮距处.最大垂向力计算公式为
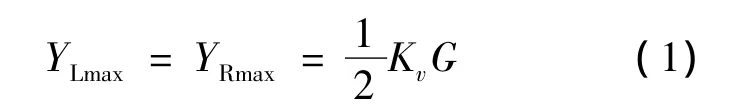
式中,YLmax、YRmax为施加在左、右空气弹簧座上的最大垂向力;G为提升桥壳满载载荷;G=7500 kg×9.81 N/kg=73 575 N;kv为动载荷系数,kv=2.5.
代入数值计算得出:YLmax=YRmax=9168.75 N.
(2)工况二:紧急制动时桥壳承受最大制动力
整车在满载高速行驶并紧急制动时,左、右提升桥车轮除受到地面作用到车轮的垂向反力外,还受到地面对提升桥车轮的制动力[8].提升桥壳在该工况下受力的组合公式为
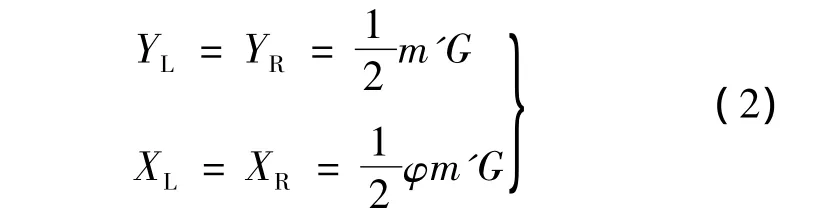
式中,YL、YR为地面对提升桥左、右车轮的垂向反力;XL、XR为地面对提升桥左、右车轮的最大制动力;G为提升桥壳满载载荷,与式(1)同值;φ为提升桥车轮与路面的附着系数,φ=0.68;m'为整车制动时的质量转移系数,m'=0.8.
代入数值计算得出:YL=YR=29430 N;XL=XR=20 012.4 N.
由于提升桥壳在该工况下的特殊性,需要施加由最大制动力产生的转矩,其转矩计算公式为:
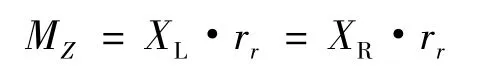
式中,XL、XR为地面对提升桥左、右车轮的最大制动力;MZ为由最大制动力产生的转矩;rr为车轮滚动半径.
代入数值计算得出:MZ=10 906.76 N·m.
(3)工况三:侧滑时桥壳承受最大侧向力
整车在满载高速行驶急速转弯发生侧滑时,整车处于侧翻的临界状态,与侧滑方向相反的车轮的垂向反力和侧向力等于零,侧滑方向的车轮的垂直反力和侧向力达到最大值,即提升桥的全部荷重由侧滑方向一侧的提升桥车轮承担[9],此时不存在纵向力.提升桥壳在该工况下受力的组合公式为

式中,YL'、YR'为整车向左、右侧侧滑时,地面对提升桥侧滑一侧车轮的最大垂向反力;ZL、ZR为整车向左、右侧侧滑时,提升桥壳承受的最大侧向力;G为提升桥壳满载载荷,与式(1)同值;φ'为整车发生侧滑时,车轮轮胎与地面间的附着系数,φ'=1.0.
代入数值计算得出:YL'=YR'=73 575 N;ZL=ZR=73 575 N.
1.3.2 边界条件及加载方式的确定
本文载荷计算方式是按照集中力的形式,由ANSYS分析软件显示所要加载位置上的所有节点个数,进而计算出相关节点的平均受力,直接施加到节点上.由于SOLID95号单元存在X、Y、Z三个方向的自由度,即各工况下提升桥壳的加载方式和约束条件分别如表1和表2所示.

表1 各工况下提升桥壳的加载方式
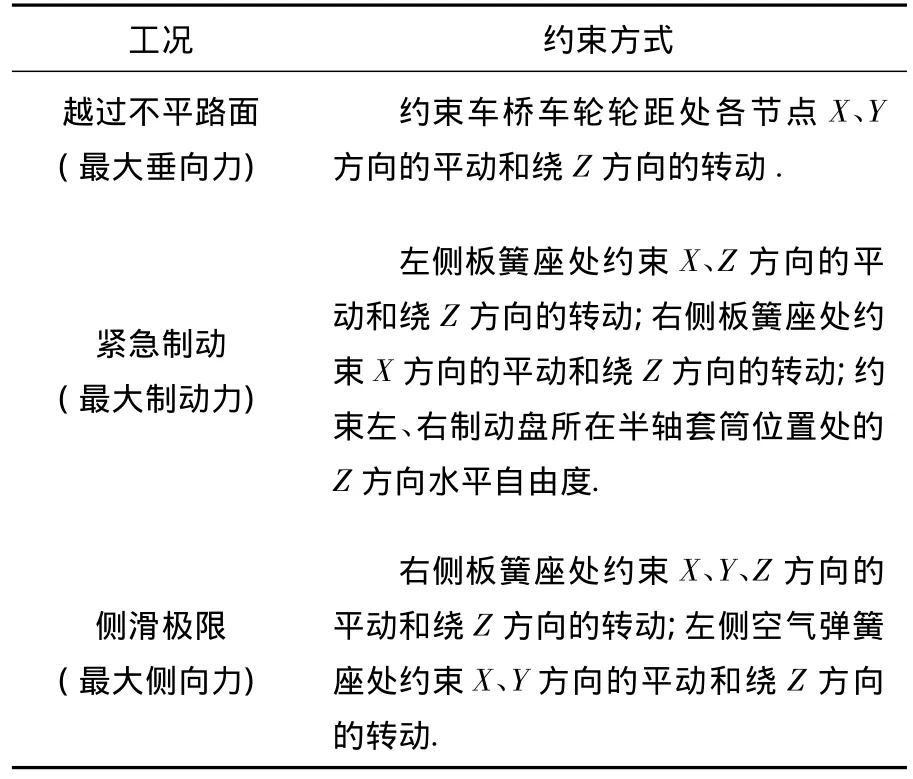
表2 各工况下提升桥壳的约束方式
2 仿真计算结果及分析
2.1 工况一:越过不平路面时桥壳承受的最大垂向力
整车的提升桥满载载荷为73 575 N,越过不平路面时的载荷按照2.5倍满载荷加载到桥壳上,桥壳只承受最大垂向力,提升桥壳的应力和变形如图3所示.
从图3(a)中可以看出应力主要出现在提升桥壳两侧板簧座所在位置的内侧凹曲面处,而最大应力出现在处轮毂所在位置上的半轴套筒第二台阶过渡处.其最大应力值为 453 MPa,小于40MnB材料的许用应力523 MPa.从图3(b)中可以看出提升桥壳最大变形量发生在桥壳中央凹曲面处,其最大变形量为14.743mm,则每米轮距变形量为14.743mm/2.372 m=6.215mm/m.目前国家标准[10]是针对驱动车桥承受满载轴荷情况,桥壳的最大变形量不得超过1.5mm/m,承受2.5倍满载轴荷时,桥壳不能出现断裂和塑性形变.对提升桥壳变形量尚无国家标准要求.

图3 工况一下提升桥桥壳的应力和变形图
针对图3所显示的数据结果进行综合分析,造成桥壳应力值与变形值均较大的原因是,在此工况中忽略了由于该车桥在实际应用中存在下板簧座,下板簧座处安装有钢板弹簧,两侧钢板弹簧通过前、后支架固定安装在车架上,构成悬架系统,也就是说,在提升桥壳两侧下板簧座处会有向上的作用力,该力会抵消一部分的最大垂向力.那么最终的实际应力和变形会更小.
2.2 工况二:紧急制动时桥壳承受最大制动力
整车在满载的状态下紧急制动时,提升桥壳主要承受垂向力和最大制动力.其应力与变形如图4所示.

图4 工况二下提升桥桥壳的应力和变形图
从图4(a)中可以看出最大应力出现在提升桥的制动盘所在半轴套筒位置处,其最大值为166 MPa,小于40MnB材料的许用剪切强度490 MPa.该工况下,桥壳在两侧板簧座位置外侧部分承受由制动力引起的力矩,由于制动力矩只对板簧座到桥头的制动盘内轴承之间的这一段桥壳产生强度效应.因此,桥壳在制动作用下,最大应力发生在提升桥的制动盘所在半轴套筒位置附近.从图4(b)中可以看出提升桥壳最大变形量发生在桥壳半轴套筒的两端,其最大变形量为0.623mm,相应的每米轮距变形量为0.263mm/m,满足国家标准.
2.3 工况三:侧滑极限时桥壳承受最大侧向力
此工况下,整车处于侧滑临界状态,只有侧滑一侧车轮承受全部的提升桥载荷以及该侧所承受的最大侧向力.由于整车承受的侧向力达到地面给车轮的侧向反作用力的最大值即侧向附着力,提升桥这种极限情况对后置提升桥的强度极为不利.过大的侧向力就容易造成侧翻的现象,应避免发生.桥壳应力与变形如图5所示.
图5 工况三下提升桥桥壳的应力和变形图
从图5(a)中可以看出,车桥的应力主要出现在车桥侧滑一侧以及桥壳中央凹曲面处,而另一侧基本没有什么变化.在侧滑方向左侧板簧座处存在着较大应力,最大应力出现在轮毂所在位置上的半轴套筒处,其最大值为199 MPa,小于材40MnB材料的许用应力523 MPa.图5(b)显示最大变形量为1.063mm,相应的每米轮距变形量为0.448mm/m,满足国家标准.图5反映出侧滑一侧车轮内侧半轴套管与方形壳体过渡区的应力集中,这主要是由于侧滑一侧车轮轮距处承受垂向反力引起的.
3 结论
(1)基于有限元分析对北奔重汽车桥有限公司某型号提升桥壳在三种典型工况下的载荷进行计算,总结出载荷、约束施加的处理办法,最后得出受力和变形结果如表3所示.

表3 各工况下提升桥壳受力和变形结果
(2)基于有限元分析对提升桥壳的结构设计及工作性能得出如下结论:
①综合三种工况下的数据结果得知,12mm厚度的桥壳本体是完全符合桥壳结构强度的要求;②根据结构力学理论,提升桥壳中央凹曲面处的落差值较大也是导致工况一下的应力值与变形量较大的重要原因之一,要根据整车配合情况,适当的减小凹曲面处的落差值;③本文中取强度安全系数n=1.5,由于目前重型汽车桥设计强调轻量化,所以一般安全系数取得较小,多接近极限设计.根据文献[11]虽然车桥不至于断裂,但安全系数偏小.因而,原材料的选取、制备到制造加工过程中,必须对质量进行严格控制;④根据较为危险工况一的数据分析,为了确保安全,重卡在执行满载作业时,应尽量避免在恶劣的不平路面上高速行驶;⑤通过对计算结果和相关文献数据比较,可以确认,在静力载荷工况下,车桥桥壳的最大应力通常发生在空气弹簧座附近和轮毂内轴承圆角处[12].
(3)本文是在不考虑焊接接触情况下对提升桥壳进行静态特性模拟仿真,所以会存在一定的误差.为此,在以后的工作中应该对该桥的焊接接触以及动态特性作进一步的分析研究.
[1]任卫群,金国栋.系统仿真技术与汽车设计制造[J].计算机仿真,1997,16(3):53-54.
[2]唐述斌,谷菊.EQ1090E汽车后桥壳轻量化的有限元分析[J].汽车科技,1994(6):12-14.
[3]朱帅,钱立军.基于ANSYS的前桥强度分析[J].机械研究与应用,2007,20(2):44-45.
[4]刘惟信.汽车车桥设计[M].北京:清华大学出版社,2004.
[5]杨万凯.汽车可靠性理论[M].北京:人民交通出版社,1986.
[6]高耀东,刘学杰,周可璋.机械工程应用精华30例[M].北京:电子工业出版社,2010.
[7]孙运柱.轻型卡车前桥前梁的设计计算[J].机械与电子,2009,31:449-450.
[8]苏恩生.汽车驱动桥壳的有限元建模与分析[D].吉林:吉林大学,2005.
[9]朱茂桃,陈昆山.农用运输车后桥壳体的结构强度分析[J].农业机械学报,2001(2):21-23.
[10]郭熹晨.QC/T 534-1999汽车驱动桥台架试验评价指标[S].北京:中华人民共和国汽车行业标准,2005.
[11]赵经文,王宏钰.结构有限元分析[M].北京:科学出版社,2001.
[12]阂鹏,孙启会.桥壳有限元模型建立及分析探讨[J].重型汽车,1999,54:19-20.
