不同核函数SVM在居民出行方式预测模型中的应用

许 铁,高林杰,景 鹏,陈东清

(1.福建交通职业技术学院,福州350007;2.上海交通大学交通运输工程研究所,上海200052;3.福州大学管理学院,福州350002)

0 引言

当前城市交通拥挤状况日益严重,这对城市交通规划、交通需求预测提出新的挑战。居民出行构成了城市交通需求的基础,为研究此问题,交通部门需对居民出行方式进行调查。居民出行调查是指对交通规划区域居民在一定时间内的个人与家庭属性、社会经济属性以及出行方式进行调查,其目的是掌握居民出行的流向、流量和出行方式等。居民出行调查可收集交通规划中需要的基础信息,是进行交通需求预测和制定交通规划方案的重要依据。

然而由于居民出行调查中存在较多不可控制的因素,各分区的抽样率总存在差异,而且抽样调查数据也具有特殊性,如何用少量的抽样数据分析出代表普遍规律的出行特征,成为许多学者研究的重点。赵贝等(2010年)利用自组织理论对居民出行方式结构进行研究,指出自组织原理对居民出行方式选择系统具有适用性[1]。鲜于建川等(2010年)利用递归联立离散选择模型研究了居民出行方式,研究结果对于出行需求预测具有指导意义[2]。冯树民,慈玉生(2010年)利用BP神经网络对居民出行产生量进行预测[3]。冯忠详,刘浩学等(2010年)利用非集计方法构建了农村人口的出行方式选择模型[4]。

但是由于居民出行方式选择是一个典型的非线性系统,受到影响因素众多,建模相对复杂。支持向量机(Support Vector Machine,SVM)产生于20世纪90年代,是非线性建模的数据挖掘方法该方法可避免人工神经网络可能陷入局部极小点、网络结构难于确定的缺点,具有更强的泛化能力,适合分析居民出行方式选择这种复杂的行为。传统关于SVM的参数选择更多采用反复凑试的方法,来取得较好的模型效果,存在较大随机性,且工作量较大。本文采用网格搜索方法选取支持向量机的参数,在一定程度上解决了参数选择的随机性,构建了居民出行方式选择预测模型,并通过福州市居民出行专项调查数据进行实证研究,为研究居民出行方式提供了新的思路;同时采用不同的核函数,对比不同核函数的分类精度、模型估算时间,为选择支持向量机核函数提供参考。

1 基于支持向量机的分类模型

1.1 基于支持向量机的居民出行方式选择模型

支持向量机(Support Vector Machine,SVM)是Vapnik教授等人在20世纪90年代提出的一种新的统计机器学习理论[5],它是在小样本情况下发展起来的,核心思想为寻求结构风险最小化。该方法通过非线性变换,在高维特征空间中把研究问题线性化,而得到的却是原样本空间中问题的非线性解,是一种非线性系统建模的新方法,克服一些传统机器学习方法的不足。支持向量机模型主要用于回归和分类,本文重点探讨用于分类的支持向量机模型。

居民出行常见的出行方式不多,通过分析居民出行方式的影响因素,设计一定的调查问卷,就能获取居民出行的相关信息,收集的数据格式如表1。通过研究个体的出行方式,构建居民出行方式选择模型,如果构建的模型能够准确对居民出行方式进行划分,则可用于预测居民出行方式,这对于研究居民出行方式选择具有适用性。

表1 居民出行调查数据

基于支持向量机的居民出行方式选择模型的任务就是要寻找一个分类机,根据已有的m个数据,模拟居民出行方式选择的规律,并能够对新的样本进行较准确地分类。依照支持向量机的理论,可把m个样本看成是n维空间的点,如何在这n维空间中寻找超平面,尽可能准确地把这些点分开。同时对于一个新的样本,也能准确划分,成为研究的重点。以下重点介绍支持向量机是如何寻找最优超平面的。

1.1.1 二分类线性可分的标准最优分类面

支持向量机理论是从线性可分情况下的最优分类平面发展起来的,也是统计学习理论中最实用的部分[5]。对于给定的训练样本集 (x1,y1),(x2,y2),…(xi,yi),其中 xi∈RN为N 维向量,yi∈{-1,1}在线性可分的情况下,在特征空间中构造多个分割平面,这个超平面被定义为:

同时,这个分类面能将两类(1,-1)无误差地完全分开,即满足:

在满足上述条件所有的分类面中,查找最优超平面,这个最优超平面满足两类的分类空隙dist最大,即每类距离超平面最近的样本到超平面的距离之和最大。这个距离可表示为:

所以,求解最优超平面问题等价于在式(2)约束条件下,求式(3)的最大值,这样建立线性支持向量机的问题转化为求解式(4)二次凸规划问题:

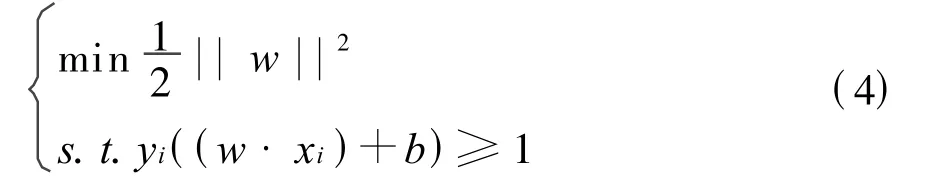
该约束优化问题可以用Lagrange方法求解,得到最优超平面决策函数为:

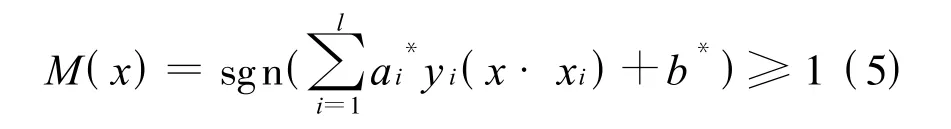
1.1.2 二分类线性不可分的情况

对于线性不可分的问题,Vapnik等人成功地引入了核空间理论,将低维输入空间的数据通过非线性映射函数映射到高维属性空间,从而把分类问题转化到高维属性空间进行,大多数输入空间线性不可分问题在属性空间可以转化为线性可分问题。为了避免高维空间中的复杂计算,支持向量机采用了一个核函数k(x,y)代替高维空间中的内积运算φ(x)·φ(y),引入松弛变量,优化问题为:

引入拉格朗日函数将式(6)转换为对偶形式:

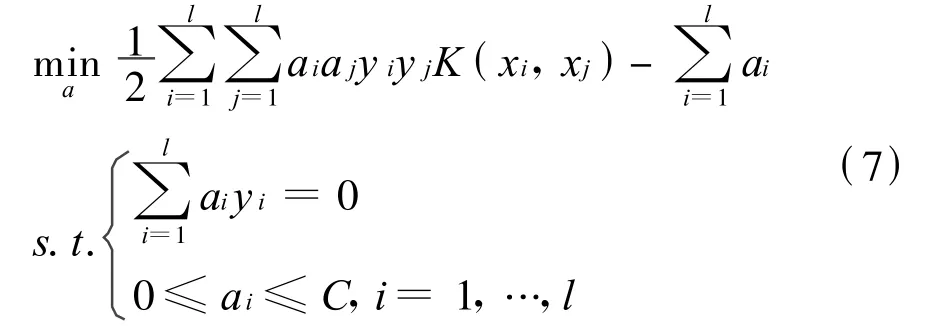
1.1.3 居民出行方式的分类

居民出行方式选择属于多分类的问题,可转换成多个二类划分问题解决。对应的每个二分类的决策函数为:

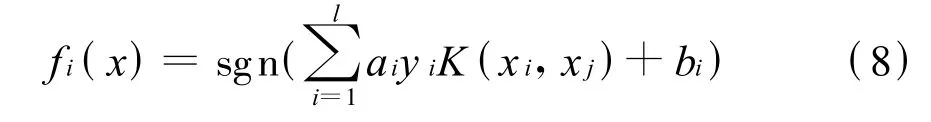
如果 fi(x)=1,则 x属于第i类,如果 fi(x)=-1,则x不属于第i类。故可得到多分类问题的总判别函数为:

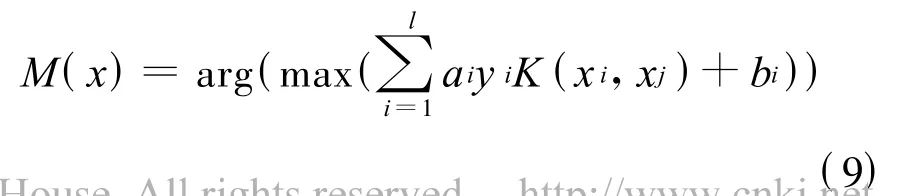
式(9)中,arg为选取指标函数,含义为:选取样本点x对于决策函数fi(x)中值最大函数的指标i对应的类,作为样本点所应该归属的类。

在居民出行方式选择中,可对居民常见的几种出行方式分别赋予类别标志,如把步行标识为1,电动车标识为2,公交车标识为3,私家车标识为4等等,构造4个二分类器,通过总判别函数就可以识别居民出行方式,例如:若 fi(x)=-1表示不属于这种出行方式;若 fi(x)=1,M(X)=1,则代表属于步行出行方式。

1.2 核函数选择及参数选择

对于支持向量机分类器而言,核函数是决定分类器性能的关键因素,对函数的估计精度和速度都有一定的影响。常见的核函数类型有:线性核函数、多项式核函数、径向基核函数RBF、Sigmoid核函数等[6]。核函数可分为2类,全局核函数和局部核函数。全局核函数具有全局性,相距很远的数据点都可以对核函数的值产生影响,泛化能力强,但是学习能力较弱,如线性核函数、多项式核函数、Sigmoid核函数;局部核函数具有局部性,只有距离较近的数据对核函数的值才有影响,学习能力强,但是泛化能力较弱,如径向基核函数RBF。本文将重点探讨这几个核函数在居民出行预测模型中的应用,分析它们的影响。

支持向量机的性能受到惩罚系数c的影响,在确定了核函数类型之后,还受到核参数(统一用 g表示)的影响。本文采用网格搜索方法进行参数探索,把交叉验证意义下的支持向量机分类正确率作为目标函数,借助计算机强大的运算功能自动选择参数,得到最优值下的惩罚系数值、核函数参数值,利用得到的参数重新训练和测试模型,如果都能得到较好的预测精度,则得到满意的模型,否则重新分析问题的影响因素,再次建模,直至得到满意的模型。

网格搜索方法即把惩罚系数、核参数设置在一定范围内,记,c∈(2m,2n),g∈(2p,2q),其中,m ＜n,p＜q。通过组合,可以得到数组(c,g),计算每一组(c,g)下的分类正确率,得到最高分类准确率下的参数(cbest,gbest),并用这组参数重新训练模型。

2 实证研究

2.1 数据来源

福州市是福建省省会,地处我国东南沿海,是海峡西岸经济区三大中心城市之一。近年来,福州市社会经济发展迅速,城市人口不断增长,但城市交通矛盾日益尖锐,交通问题成为一个亟需解决的难题。为了更加合理地规划城市交通系统,2008年福州市交通部门进行了居民出行专项调查。本文通过数据预处理,选取了600个有效调查样本进行实证分析,部分居民出行调查数据如表2所示,相应变量说明如表3所示。

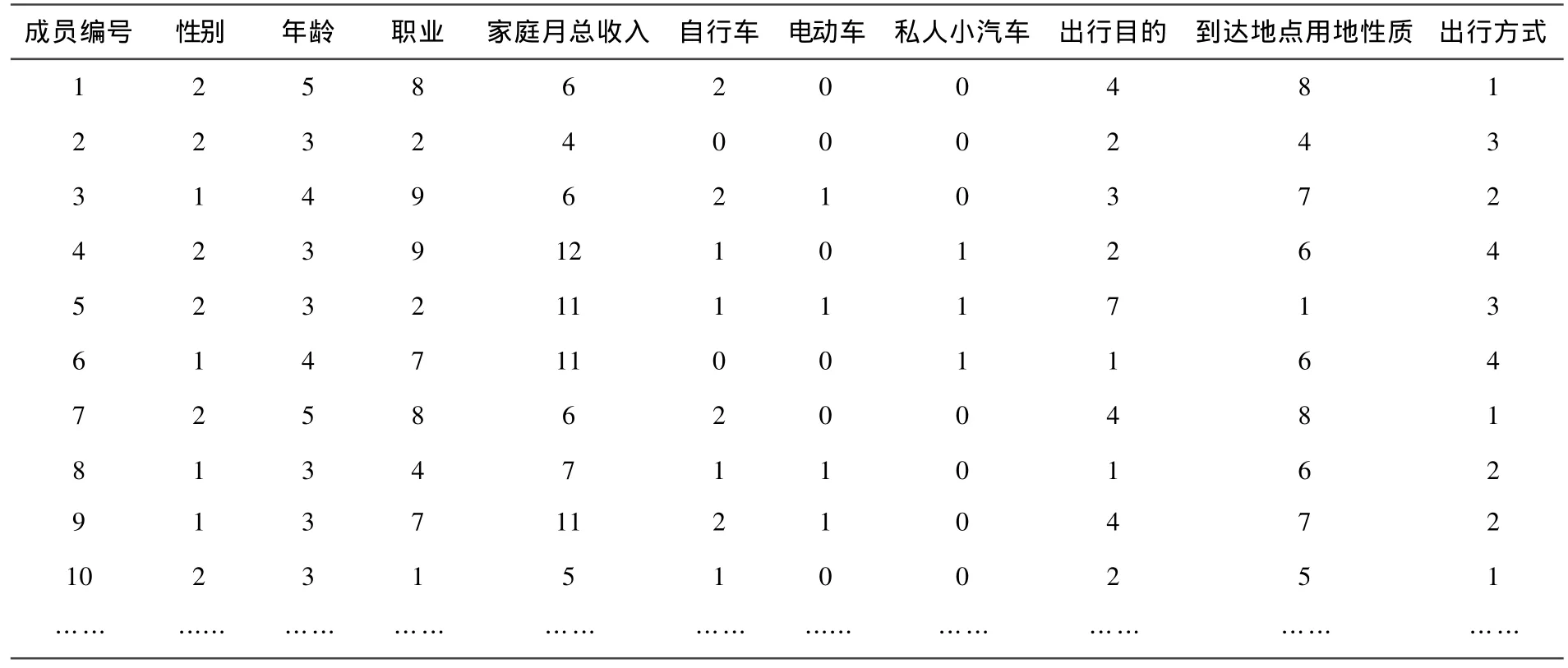
表2 2008年福州市居民出行调查部分数据

表3 各变量说明表

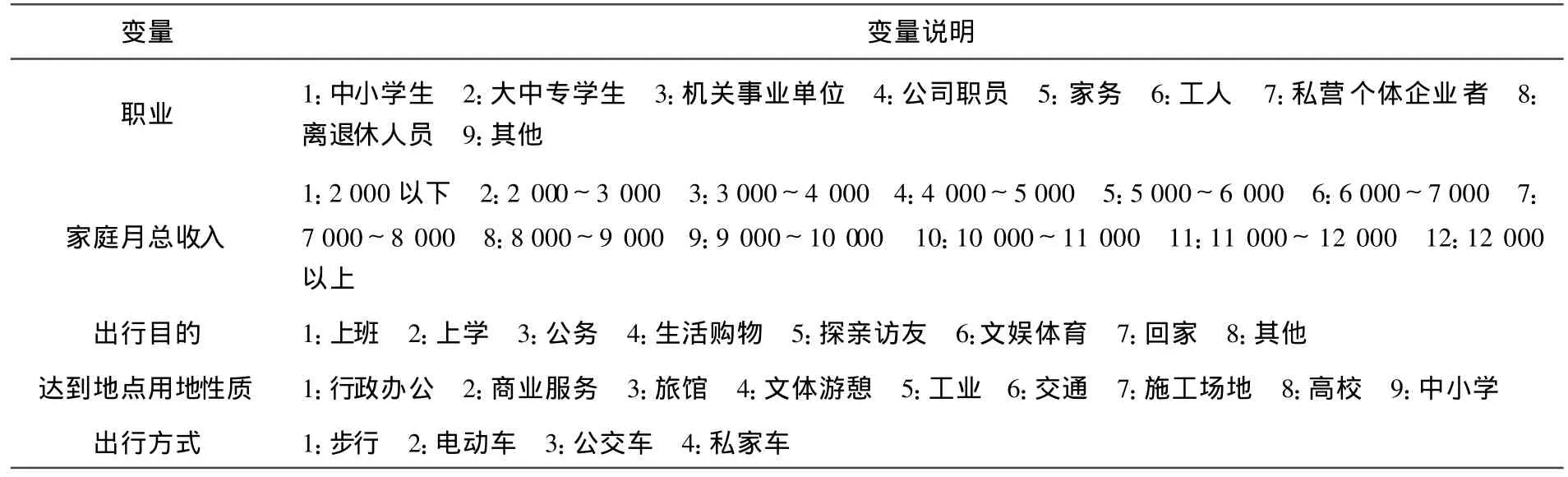
变量变量说明职业 1:中小学生 2:大中专学生 3:机关事业单位 4:公司职员 5:家务 6:工人 7:私营个体企业者 8:离退休人员 9:其他1:2 000以下 2:2 000～3 000 3:3 000～4 000 4:4 000～5 000 5:5 000～6 000 6:6 000～7 000 7:达到地点用地性质 1:行政办公 2:商业服务 3:旅馆 4:文体游憩 5:工业 6:交通 7:施工场地 8:高校 9:中小学出行方式 1:步行 2:电动车 3:公交车 4:私家车家庭月总收入

2.2 数据预处理

把600个样本分成2部分,其中的450个样本作为建模样本,150个样本作为测试样本。以性别、年龄、职业、家庭月总收入、自行车拥有量、电动车拥有量、私人小汽车拥有量、出行目的以及到达地点用地性质作为输入,以出行方式作为输出训练模型。考虑到变量之间存在量纲的差别,以及个体之间存在较大差异,对数据进行了标准化处理。本文把数据规整到[-2,2]之间,公式如下:

通过上式把变量规范化到[-2,2]之间,其中xmin为变量X的最小值,xmax为变量X的最大值。

2.3 模型结果分析

利用Matlab 2009b编程实现模型计算,4种不同核函数的分类精度如表4所示,模型估计时间如表5所示。

表4 不同核函数SVM模型分类结果

分类精度是衡量本文构建的居民出行方式预测模型的重要指标,含义为:模型分类结果中被正确划分到某个类别的样本占所有分类样本的比重。计算公式如下:

如RBF核函数的建模样本的分类精度为86.22%,也就说在450个建模样本中,有388个样本被正确划分到所属类;测试样本的分类精度为81.33%,即在150个测试样本中,有122个样本被正确划分。

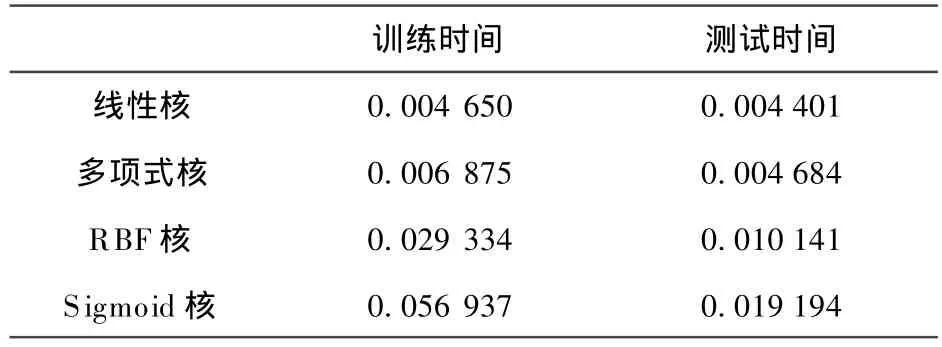
表5 不同核函数SVM模型计算时间/s

以上训练时间是指用网格搜索方法探索出最优参数后,用选择出来的惩罚系数C,核函数参数g进行模型训练所用的时间;测试时间指的是,用最优参数进行模型测试所花的时间。从表5中可以看出,线性核函数训练时间和测试时间都是最短的,而Sigmoid核却是最长的。这4个核函数对SVM模型的估计时间都很短,相差较小,但是如果选择网格搜索方法、遗传算法、粒子群优化算法等进行参数选择,程序的运行时间将会存在较大差异。

由表4可知,多项式核函数和RBF核函数相对于其他2个核函数在分类准确率上具有明显优势,多项式核函数属于全局性核函数,学习能力相对于RBF核函数较弱,但是泛化能力却比 RBF核函数更强;而RBF核函数是局部性核函数,学习能力强,泛化能力相对较弱,但相差不多,而学习能力明显比多项式核函数高。从表5中,看出Sigmoid核的计算时间最长,线性核函数时间最短。Sigmoid核函数在4个核函数中,建模分类精度及测试分类精度都是最低的,这是因为只有当核函数对应的矩阵为对称、半正定矩阵时才能满足 Mercer条件,Vapink[7]曾指出,在Sigmoid核函数中,当参数取特定特值,Sigmoid核对应的和矩阵非半正定,故在核函数的选择中,不优先使用Sigmoid核函数。结合表4、表5可知,在支持向量机模型的构建中,关于核函数的选择优先考虑RBF核函数,该核函数的学习能力、泛化能力都较强,其次考虑选择多项式核函数。

从模型计算结果可以看出,支持向量机方法对居民出行方式选择具有较好的拟合效果,采用多项式核函数、RBF核函数构建的模型,建模样本和测试样本的分类精度均达到80%以上,支持向量机方法在居民出行方式选择预测中,有较高精度,利用本文构建的居民出行方式选择模型,能够较准确预测居民的出行方式,这对于规划居民小区交通,合理配置交通系统有参考价值。

3 结语

居民出行方式的选择受到多方面因素影响,是一个典型的非线性问题。支持向量机方法源于统计学习理论,经过非线性映射,把样本空间映射到高维特征空间,在高维特征空间利用一个线性超平面实现线性划分。借助Mercer核展开定理,通过升维,在高维空间把非线性问题转化为线性问题,为预测居民出行方式提供了新的思路,通过本研究得出以下结论。

(1)本文利用多项式核函数、RBF核函数的支持向量机方法构建了居民出行方式的选择模型,建模样本和测试样本的分类精度均达到80%以上,分类的效果较好。所构建的模型,能应用于居民出行方式选择的预测,这对城市规划交通系统有现实指导意义。从另一方面也说明了居民出行方式选择不仅受到个人属性特征的影响(性别,职业等),还受到家庭属性(拥有的交通工具、家庭收入),以及出行目的等因素的影响,这是一个复杂非线性的系统,支持向量机理论适合这类问题的研究。

(2)在支持向量机模型的构建中,关于核函数的选择优先考虑RBF核函数,该核函数的学习能力、泛化能力都较强,其次考虑选择多项式核函数。在今后的研究中,可考虑混合核函数的研究,构建新的核函数,综合发挥RBF核函数学习能力强的优势以及多项式核函数泛化能力强的特性,提高支持向量机的性能。

[1]赵贝,赵淑芝.基于自组织理论的居民出行方式结构模型[J].吉林大学学报:工学版,2010,40(6):1523-1527.

[2]鲜于建川,隽志才.出行链与出行方式相互影响模式[J].上海交通大学学报,2010,44(6):792-796.

[3]冯树民,慈玉生.居民出行产生量BP神经网络预测方法[J].哈尔滨工业大学学报,2010,42(10):1624-1627.

[4]冯忠详,刘浩学.农村人口出行方式选择模型[J].交通运输工程学报,2010,10(31):77-83.

[5]王定成.支持向量机建模预测与控制[M].北京:气象出版社,2009:1-18.

[6]奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用,2011,47(3):122-123.

[7]VAPNIK V.The nature of statistical learning theory[M].New York:Springer-Verlag,1995:25-37.