Fourier-M ellin矩在图像识别中的应用

马自萍

（北方民族大学 信息与计算科学学院，宁夏 银川 750021）

矩特征具有很好的描述物体形状能力，广泛应用与图像识别、图像检索等领域。所以如何研究具有旋转、平移、放缩不变性的矩和矩的快速计算成为了近几十年的研究热点。正交的Fourier-Mellin矩 （Orthogonal Fourier-Mellin moments（OFMMs））是被沈和申[1]提出的，这种矩利用一系列正交极坐标多项式Qn（r）定义，在图像描述和噪声敏感性方面，比正交Zernike矩（ZMS）处理具有更好的操作性。在小的极坐标距离区域，第一种方法的正交极坐标多项式比第二种方法有更多零点。例如其他正交矩[2]是基于正交特性，一系列Fourier-Mellin矩能使用最少的信息量来描述物体。这种矩有旋转不变性，并能描述图像的空间成分，由于这个特性，OFMMs常常被应用于图像处理和模式识别[3-7]。

传统的方法是通过极坐标下计算正交多项式OFMMS的方法，虽然二维的傅立叶米兰矩是在极坐标下计算，具有对称性和旋转不变性这种方法，但是由于要把笛卡尔坐标系下的图像转换到极坐标下，所以产生数字和几何误差。这些误差耗费了大量的运算时间，尤其是在矩的阶数较高时。所以对于真实时间应用性具有不可实践性。为了避免这种误差，有人提出了直接在笛卡尔坐标下计算OFFMs[8]，并用于重建。本文为了OFFMs在笛卡尔坐标和极坐标下的计算和重建差别，进行了试验。

1 极坐标下Fourier-M ellin矩的定义

极坐标下Fourier-Mellin矩（OFFMS）用于计算正交多项式 Qn（r）

其中：

多项式 Qn（r）定义于 0≤r≤1，由正交性可得：

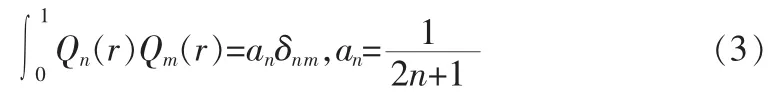
OFMM在极坐标下定义如下：

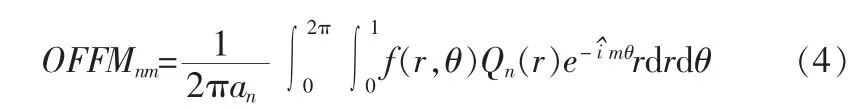
极坐标下，重建图像计算式为：

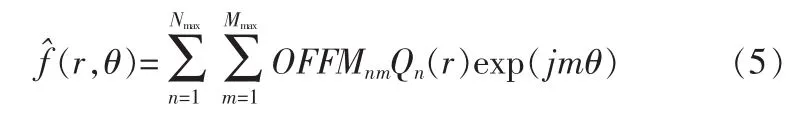
2 笛卡尔坐标下OFFM矩的定义

在极坐标和笛卡尔坐标下，有下列关系式：

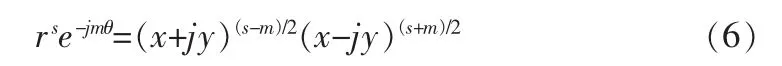
由于

可以得到下式

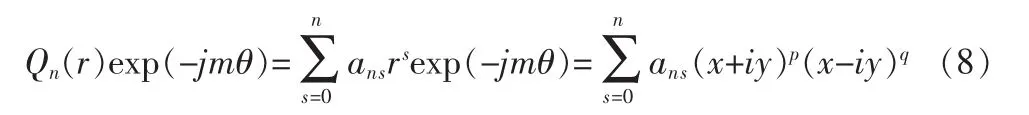
此时 p=（s-m）/2，p=（s+m）/2， 可以得出笛卡尔坐标下OFFM矩[8]。

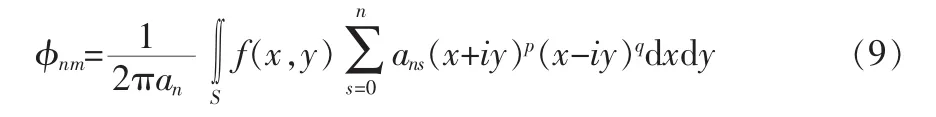
笛卡尔坐标下OFFM矩的重建图像f（x，y）为：

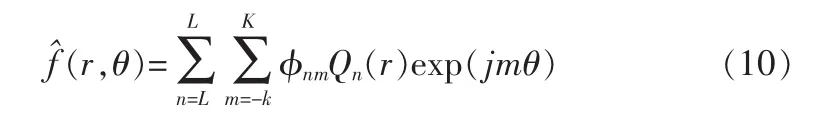
其中L，K分别为θ和r离散化的最大值。上式可以直接利用直角坐标下的OFFM矩进行重建，避免了直角坐标向极坐标转换时产生的误差，提高了重建精度。

3 实验

3.1 重建试验

文中利用式（5）和（10）分别实现了OFFM在不同阶数下的重建效果，结果如图1所示。

3.2 抗噪性能试验

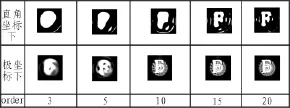
图1 不同坐标下对字母“F”的重建效果Fig.1 Reconstructed image of letter“F” in two coordinates

ALOI（ the Amsterdam Library of Object Image）是包含各种形状的彩色物体图像库，包含ILL（illumination direction），COL （illumination color），VIEW（object viewpoint）3 个子库，从ILL库中选出一 张二维彩色图像，对图像按照噪声密度分别为 0.01，0.02，0.03，0.04，0.05 时加入 salt&pepper噪声，得到图像如图2所示作为测试图像序列。

图2 不同噪声密度下的图像Fig.2 Noise density of origine image added salt&pepper

其中fmi，i=1，2，…5是图中各个图像的OFFM矩特征向量，fm1是原图像的OFFM矩特征向量。在不要阶数下各个图像的相对误差试验图如3所示。从图中可以看出，噪声密度对OFFM矩特征向量的计算误差差别不太明显，说明OFFM矩对噪声有很好的鲁棒性。

对图2中不同噪声图像的计算相对误差采用如下公式：

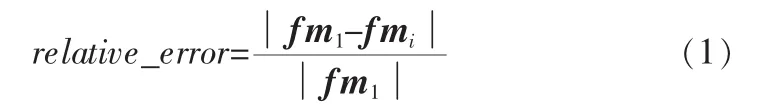
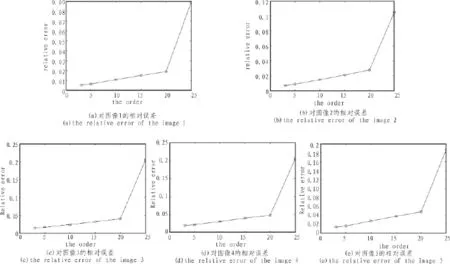
图3 不同阶数下对噪声图像的相对计算误差Fig.3 Relative error of the noise images in figure 2

3.3 分类试验

选择3类子库ILL，COL，VIEW图像各1200张，计算OFFM矩，并利用KNN分类试验，结果如下：

图4 在不同图像库中的分类Fig.4 Classification results of OFFM in different databases

4 结束语

文中从矩的计算方法、重建方法、噪声敏感程度对OFFM矩进行研究，并在图像识别应用中，验证特性。在实现了两种坐标下的计算和重建，并对OFFM在不同噪声图像进行试验，从实验可以看出，在相同阶数下，直角坐标下图像重建更清晰，具有更小的重建效果。OFFM矩具有良好的抗噪性能。

[1]Sheng Y，Shen L.Orthogonal Fourier-Mellin moments for invariant pattern recognition[J].J.Opt.Soc.Am.A.1994，11（6）:1 748-1 757.

[2]Teague M.Image analysis via the general theory of moments[J].J.Opt.Soc.Am.1980，70（8）:920-930.

[3]Terrillon J C，McReynolds D，Sadek M，et al.Invariant neuralnetwork based face detection with orthogonal Fourier-Mellin moments[C]//In:Proceedings of the 15th IEEE International Conference on Pattern Recognition，2000:993-1 000.

[4]Kan C，SrinathMD.Invariantcharacter recognitionwith Zernike and orthogonal Fourier-Mellin moments[J].Pattern Recognize，2002，35（1）：143-154.

[5]Andrew T B J，David N C L.Integrated wavelet and Fourier-Mellin invariant feature in fingerprint verification system[C]//Proceedings of the 2003 ACM SIGMM Workshop on Biometrics Methods and Applications，2003:82-88.

[6]Wang X，Xiao B，Jian-Feng M，et al.Scaling and rotation invariant analysis approach to object recognition based on Radon and Fourier-Mellin transforms[J].Pattern Recognize，2007，40（12）:3503-3508.

[7]Jiu-bin T，Lei A，Ji-wen C，et al.Sub-pixel edge location based on orthogonal Fourier-Mellin moments[J].Image Vis.Compute.2008， 26（4）:563-569.

[8]HU Hai-tao，PING Zi-liang.Computation of orthogonal Fourier-Mellin moments in two coordinate systems[J].J Opt.Soc.Am，2009，26（5）:1080-1084.