两种常见的状态方程及其特征向量的正交性

张 淼,陈庆文

(1.长春工程学院理学院,长春130012;2.解放军装甲兵技术学院基础部,长春130117)

近年来,除了在现代控制理论中,状态空间格式还在另外两个领域中得到了广泛的发展和应用,一个是多自由度系统的结构动力响应分析,另一个是与灵敏度分析相关的结构动力修改、结构集成和结构再设计等。结构动响应分析的方法中,状态空间法、复模态法及一阶常微分方程组的初值解法[1]这三种方法都是在状态方程中进行分析和求解响应的,而直接积分法既可以在状态方程中,也可以直接对系统运动的平衡方程对时间步长Δt进行数值积分计算响应,所以状态方程只是其可选择的模式之一[2]。在灵敏度分析的相关领域中,模态分析是其重要的基础[3],而各种类型的模态向量之间的关系及作用都需要将振动系统转化到状态空间中分析,这在讨论特征向量的一阶、二阶导数及状态方程的解耦等问题时,具有很高的理论和应用价值,可以为系统的参数识别、模型修正[4]及损伤识别[5]等工程应用提供保障。如今状态空间理论在应用过程中得到发展和完善,究其原因首先是由于状态方程具有可分离的数学结构,因此比传统的方法更为优越,特别是对于多激励输入输出系统,状态空间具有明显的优势,其次状态方程描述一个动态的过程,不论系统多复杂,状态空间的描述总是具有统一简洁的形式,并可用多种分析技术在计算机上进行数值计算.而对状态向量的正交性,它不仅是实现状态方程解耦的重要工具,而且也是理论分析的基础,但关于状态向量的正交化的总结及评述性的文献却很少见,这使得人们在应用状态空间格式时,得不到系统的理论指导,很多应用方面的文献中常常忽视推导中对系统矩阵的对称性的要求,从而容易产生混淆甚至错误。本文从上述两种结构动力学领域出发,总结在两个领域中常见的状态方程格式,介绍振动系统的特征问题与其状态方程的特征问题之间的关系,并对两种类型的状态方程的特征向量的特点及其正交性进行分析和对比,给出了特征向量正交性的证明及其求解方法。

1 线性振动系统的左、右特征向量

描述自由度为N的线性阻尼离散系统的自由振动的动力方程

其中,M、C和K ∈RN×N分别代表质量、阻尼和刚度矩阵,x(t)∈RN是广义坐标向量,t∈R+代表时间 。作拉普拉斯变换 x(t)=uest=ueiωt(s=iω),代入式(1)得:

关于式(2)的特征值si是特征多项式det[s2M+sC+K]=0的根。

对于N自由度系统,式(2)有2N个呈复共轭对出现的特征值s1,…,sN,s*1,…,s*N,或记为s1,…,sN,sN+1,…,s2N,其中s*i表示si的共轭(i=1,2,…N),称为系统的极点。这些特征值对应着一组特征向量,对多自由度系统,这些特征向量ui及u*i是复共轭对出现的,称为模态振型向量(复模态向量),模态矩阵为:

定义1 对满足下式

的si∈C,称为式(1)的第i个特征值,ui∈CN称为式(1)与si相对应的第i个右特征向量。其复共轭对也满足上式,所以将u1,…,uN,u*1,…,u统称为二阶式(1)的右特征向量系,或记为u1,…,uN,uN+1,…,u2N。

同样可以引入系统的左特征向量。

定义2 如果对vi∈CN,若满足

称v1,…,vN,v*1,…,v为式(1)的左特征向量系,或记为v1,…,vN,vN+1,…,v2N。

注:由式(3)和式(4)可知,当M、C和K 为对称阵时,式(1)的左、右特征向量是相同的,但当M,C和K不是一般的对称矩阵时,情况则相反。

式(1)的左、右特征向量既可以从式(3)和式(4)中分别获得,也可以分别从一阶系统中获得,为此,可以将二阶系统(1)用状态空间法转化为一阶系统。

2 线性振动系统的形如A˙y+By=0的状态方程

在结构系统的模型修正时,基于设计参数及矩阵元素的修正算法中,可以使用无阻尼实模态的正交归一化条件作为约束求解修正量[6],最近还有一些文献[7]已开始使用复模态的正交归一化条件来设计修正算法,复模态的分析都要从状态方程出发,而经常选择的就是A˙y+By=0型的状态方程。从本文的讨论可知,这样做的原因是这种形式的状态方程不仅具有左、右特征向量的双正交关系,而且它的右特征向量系统内部就具有加权正交关系。如果使用第二种正交性,可以不必计算左特征向量系,节省工作量。另外在文献[8]中也出现了A˙y+By=0型的状态方程,下面就分别讨论这种形式的状态矩阵的左、右特征向量及其正交性。

设

代入式(1),则该二阶系统将转化为如下一阶系统:

称为系统的状态矩阵,式(5)中的向量称为状态向量,式(6)称为状态方程。

注:在系统性质矩阵M、C和K 为对称阵时,状态矩阵A和B也为对称阵,这一点在其他类型的状态方程中是很难做到的,因此它也比其他类型的状态方程多一种正交性。

2.1 状态矩阵A和B的右特征向量

作拉普拉斯变换 x(t)=uest=ueiωt(s=iω)代入式(6),则有

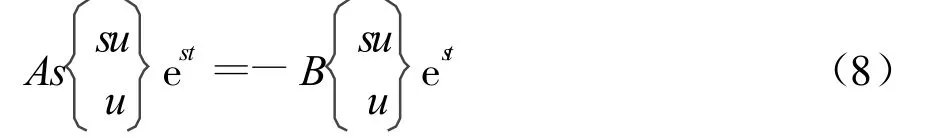
且满足

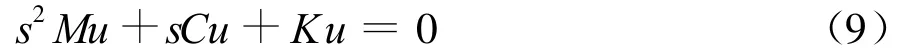
由式(8)和式(9)可知,原式(1)的振动特征问题转化为广义特征问题:

其中

称为广义特征问题式(10)的右特征向量,或称为状态矩阵A和B的右特征向量,它的后N维恰为振动式(1)的右特征向量,见定义1。

2.2 状态矩阵 A和B的右特征向量系的加权正交性

在一般黏性阻尼条件下,广义特征问题式(10)的右特征向量具有加权正交性[9]。当系统的性质矩阵M、C和K为对称阵时,对相异的特征值,如果r≠s,则有

式(12)说明,这些向量在A加权的条件下是正交的,同时可以得出这些向量在B加权的条件下也是正交的,即

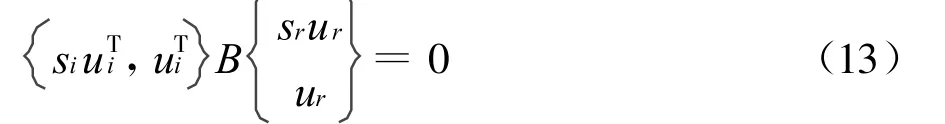
这些正交性是使系统方程解耦而进行某种坐标变换的基础。

2.3 状态矩阵A和B的左特征向量

上面讨论中获得的状态矩阵A和B的右特征向量系的正交性,其中一个重要条件就是要求系统性质矩阵M、C和K对称,在非对称系统中,那些正交性条件就不起作用了,这时为了进一步讨论,有必要引入状态矩阵的左特征向量。把式(1)变换成一阶Duncan形式式(6)后,为了表达上的简便,把与式(10)相关的右特征问题表示为

其中,sj∈C是第j个特征值,zj∈C2N是第j个右特征向量,它是与二阶系统的第j个右特征向量有关的,即

定义3 设向量yj∈C2N也与sj相联系,并满足

则称yj(j=1,…,2N)为状态矩阵的左特征向量。

为了讨论状态矩阵A和B的左特征向量yj与式(1)的左特征向量vj之间的关系,先假定yj可以表示为

其中,y1j,y2j∈ CN。把yj代入式(16)然后简化,得到:

通过比较方程式(4)和式(20),可以得到y2j=vj。因为M是非奇异的,从式(19)中得到y1j=sjvj,因此,状态矩阵的左特征向量与二阶系统式(1)的左特征向量建立联系:

2.4 状态矩阵A和B的左、右特征向量系的加权正交性

定理1 对不同的特征值,状态矩阵的左、右特征向量满足加权正交关系(又称双正交关系):

证明:对式(16)右乘zk(k≠j),可得:

将式(25)与式(24)相减可得:

当sk≠sj时,有式(22),同理有式(23),定理得证。

注:如果系统的性质矩阵M、C和K 为对称阵时,系统的左、右特征向量是相同的(见式(21)和式(15)),此时左、右特征向量的加权正交关系(见式(22)和式(23))退化为右特征向量内部的加权正交关系(见式(12)和式(13))。

3 线性振动系统的形如Ay-˙y=0的状态方程

在结构动响应分析文献[10]中常使用形如Ay-˙y=0的状态方程,这主要是由于在用直接积分法构造迭代格式时,这种类型的状态方程显然要比前一种更为简洁,另外从它的状态向量中可以很容易地同时得到各时间点上的位移及速度响应。

对线性振动系统的运动方程式(1),设

代入方程式(1),则该二阶系统将转化为如下一阶系统:

其中

称为系统的状态矩阵,式(27)中的向量称为状态向量,式(28)称为状态方程。

注:这种类型的状态矩阵(29)不是对称的,导致它的右特征向量系不是正交的,还必须要求M-1存在,但是它的优点是振动系统式(1)的特征问题转化为一般矩阵A的特征问题,而不是广义特征问题。

3.1 状态矩阵A的右特征向量

作拉普拉斯变换代入式(3),则有

且同样满足式(9),由此可知原系统式(1)的振动特征问题转化为状态矩阵A的一般特征问题:

其中

称为状态矩阵A的右特征向量,它的前N维恰为振动系统式(1)的右特征向量。

注:与前一种状态方程不同(见2.2),在一般黏性阻尼条件下,状态矩阵A的右特征向量之间不具有正交性,这是由于A不对称引起的。

为了进一步讨论正交性,引入状态矩阵的左特征向量。

3.2 状态矩阵A的左特征向量

为了表达上的简便,把方程式(32)表示为:

其中si∈C是第i个特征值,Zi∈C2N是第i个右特征向量,它是与二阶系统的第i个右特征向量有关的,即

定义4 对向量yk∈C2N,如果有

则称yk(k=1,…,2N)为矩阵A的左特征向量系。

同前面的讨论类似,我们也希望寻求状态矩阵A的左特征向量yj与系统(1)的左特征向量vj之间的关系。先假定yj也可以表示为式(17)的形式,并代入式(34),得

将式(35)解出yT1j,代入式(36)可得:

所以

本文给出的上述结论,指明了如何构造状态矩阵的左特征向量的方法,并为实现左右特征向量的归一化处理提供了便利。

3.3 状态矩阵 A的左、右特征向量系的正交性及加权正交性

定理2 对不同的特征值,矩阵A的左、右特征向量满足正交关系:

证明:对式(34)右乘Zi(i≠k),得:

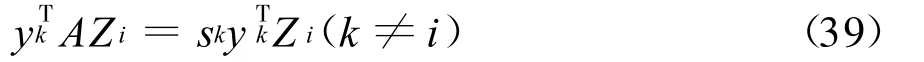
用式(39)减式(40)得:

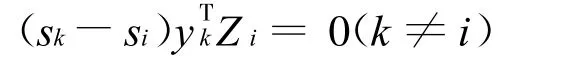
对不同特征值,由于sk≠si,所以有式(38),得证。

定理3 对不同的特征值,矩阵A的左、右特征向量满足加权正交关系:

证明:由式(41)可知,这个结论是显然的。

4 结语

首先,本文的讨论中指出在使用两种状态方程的正交关系时,必须格外注意它们与系统的左右特征向量的关系,以及系统性质矩阵的对称性等,否则极易得到错误的结论。对于形如 A˙y+By=0的状态方程,如果系统性质矩阵对称时,不仅系统的左、右特征向量相同,而且状态方程的左、右特征向量也是相同的,此时它们的双正交关系退化为状态方程的右特征向量系的内部正交关系,但对于形如Ay-˙y=0的状态方程的左、右特征向量在相同条件下不具有上述特点,而且它的右特征向量系也不具有内部正交关系。其次,本文给出了多种正交关系的证明,并提供了构造左、右特征向量的方法,使状态方程的特征问题更加明晰,也为工程应用提供了保障。

[1]郭兴旺,邹家祥.对机械振动系统的六种动态响应分析方法的评述[J].振动与冲动,1996,15(2):43-46.

[2]李红云,沈为平.结构动力响应的精细时程积分并行算法[J].上海交通大学学报,1998,32(8):81-85.

[3]M Bogomolni,U Kirsch,I Sheinman.Efficient Design Sensitivities if Structures Subjected to Dynamic Loading[J].International Journal of Solids and Structures,2006,43:5485-5500.

[4]宋汉文,王丽炜,王文亮.有限元模型修正中若干重要问题[J].振动与冲击,2003,22(4):68-72.

[5]赵红兵,孙国,顾元宪.采用新型损伤指示因子和结构优化方法的单元损伤识别[J].计算力学学报,2006,23(5):573-576.

[6]徐静.有限元模型修正法在结构动态设计中的应用[J].浙江海洋学院学报:自然科学版,2001,20(2):139-142.

[7]何建军,姜节胜.基于降阶模型的非经典阻尼结构拓扑修改的复模态重分析方法[J].振动与冲击,2009,28(7):50-54.

[8]Yeong-Jong Moon,Byoung-Wan Kim,Man-Gi Ko,etc.Modified Model Methods for Caculating Eigenpair Sensitivity of Asymmetric Damped System[J].International Journal for Numerical M ethods in Engineering,2004,69:1847-1860.

[9]沃德◦海伦.模态分析理论与试验[M].北京:北京理工大学出版社,2001:13-14.

[10]徐涛,于澜.线性振动亏损系统广义模态灵敏度的逐层递推演算方法[J].力学学报,2008,2:281-287.