基于数组的关联规则挖掘算法的研究

李 敏，潘祥光，曲云波

(1.哈尔滨商业大学计算机与信息工程学院哈尔滨 150028;2.哈尔滨工业美术设计学校，哈尔滨 150059)

当今世界，数据成为企业宝贵的资源.数据挖掘(Datamining)就是从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程［1］.关联规则是数据挖掘在商品销售领域研究的热点之一.例如在购物篮分析当中，它可以从大量的交易数据中辨别交易项目之间是否存在某种关联关系，从而得知顾客的购买习惯，这些信息可以指导商品的货架布置，生产安排等，为企业的销售决策提供支持.

关联规则挖掘过程可以分为两步:一是寻找频繁项集;二是利用频繁项集产生有价值的规则.第二步比较容易实现，当前大部分研究是针对第一步.所以，如何采用合适高效的算法找出全部的频繁项集是核心问题，是衡量关联规则挖掘算法的标准.传统的算法是经典的Apriori，之后还有其改进算法AprioriTid和AprioriHybrid.但这些算法存在以下两个缺点:1)多次扫描事务数据库，I/O时空开销大;2)可能产生庞大的候选项集，内存执行时间面临严峻挑战，整个数据库装入内存是不现实的［2］.因此相继提出了如数据分割，散列技术，抽样技术，动态项集技术等优化算法.

为了快速挖掘出频繁项集，本文在相关性质和Apriori算法的基础上，对基于数组的关联规则算法进行改进，在频繁项集进行自连接生成候选项集之前对项目计数，从而减少参与连接的项的数目，即减小生成候选项集的数量和规模，克服了Apriori需多次扫描数据库和产生大量候选集的弊端，提高了挖掘频繁项集的效率.

1 基本概念

设 Item={I1，I2，...，In}是所有项目的集合，D是相应的事务数据库，其中每个事务T是一个项目子集(T⊆I)，且具有一个惟一的标识符TID.设A是一个项目集合，称为项集.事务T包含项集A，当且仅当A⊆T.如果项集A中含有的项目个数为k，则称其为k项集.

定义1 关联规则:形如A⇒B的蕴涵式，其中 A⊂I，B⊂I，并且 A∩B=φ.

定义2 支持度:假如规则A⇒B在事务集D中成立，则支持度support定义为D中事务包含A∪B的百分比.support(A⇒B)=P(A∪B)

定义3 置信度:假如规则AB在事务集D中成立，则置信度从从confidence定义为D中包含A的事务同时也包含B的百分比，是一个条件概率.如果用support_count(A∪B)表示包含项集A∪B的事务数，support_conut(A)表示包含项集A的事务数，则

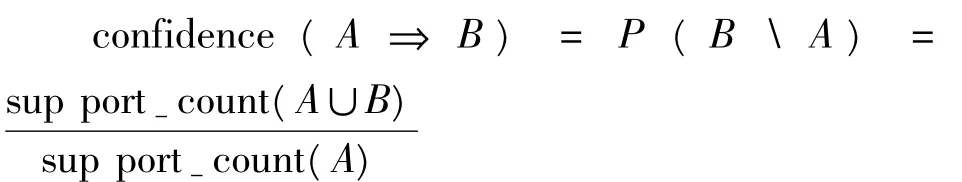
定义4 频繁项集:项的集合称为项集(itemset)，频繁项集(frequent itemset)是满足最小支持度的项集，即包含项集的事务数大于或等于min_sup与D中事务总数的乘积.

2 Apriori算法及相关性质

2.1 Apriori算法基本思想

Apriori算法是采用逐层搜索的迭代方法，自底向上的寻求数据库中的频繁项集.该算法需要多次循环，每次循环都利用上次循环产生的频繁(K－1)项集产生频繁K项集的候选项集，然后再扫描数据库来检验是否为要寻找的频繁项集.即用频繁(K－1)项集搜索产生频繁K项集.假设Ck是Lk的候选项集，不管其的成员是否为频繁的，全部的频繁K项集都包含在候选Ck当中.Ck当中的元素是否全部都为频繁项集，在验证的过程中，需要多次扫描事务数据库.大量的研究表明，频繁2项集的挖掘是Apriori算法的效率主要缺陷，当项目的数量达到一定范围，算法的复杂度将呈指数级增长，严重影响了其运行效率.如果存在1万个频繁1项集的情况下，Apriori算法需要产生多达1千万个候选2项集.如果需要发现长度为100的频繁模式，所需的候选多达1030.由此可以看出Apriori算法的两个瓶颈:

1)需要多次扫描整个事务数据库

2)识别频繁项目集时需要进行模式匹配，效率很低.

2.2 相关性质及推论

性质:设X是数据集D中的频繁K项集，则X的所有(K－1)项子集也一定是频繁(K－1)项集.

Apriori算法用这个性质用于压缩搜索空间，减少候选项集的数量.

推论1:Xk是数据集D的频繁K项集，则频繁(K－1)项集集合 LK－1中包括 Xk的(K－1)项子集的个数一定是K.

推论2:如果 Xk={X1，X2，X3，….，Xk}是数据集D的频繁K项集，则其每个元素Xi在频繁(K－1)项集集合LK－1的所有(K－1)集合中出现次数一定不小于(K－1).

由上可知某个元素要成为某个K维频繁项集中的元素，则该元素在频繁(K－1)项集集合中出现的次数一定不小于(K－1)次.所以频繁(K－1)项集在进行自连接之前统计出所有项出现的次数，然后删除频繁(K－1)项集中出现次数小于(K－1)的项集，就能够事先判断出不可能成为频繁集的连接减少相当数量的存储空间和节省大量的时间［3］.

3 改进算法的思想和步骤

在已有算法的基础上［4－6］，改进算法的基本步骤:

1)扫描数据库，根据数据库中出现的事务记录进行编码［6］，用二维数组结构保存数据，其中行表示事务信息，列表示项信息.以后的操作只针对主存对数组处理，与数据库无关.大大减少了I/O时空开销，节省了时间.

2)在由LK－1项集进行自连接，生成Ck项集的过程以前，首先是统计LK－1项集中所有项目出现的次数.根据推论2删除LK－1中出现的次数小于(K－1)次的项目集，修改后的 LK－1改为 L'K－1.L'K－1自连接生成 Ck.

3)对Ck根据Apriori算法进行剪枝得到LK，计算LK中的K项集的个数，如果项集个数小于(K+1)，则不必再进行(K+1)项集的运算，算法结束.如果不小于(K+1)，则转2).

算法主要伪代码如下:

输入:事务数据库D;最小支持度min_sup.

输出:D的频繁项集L.

InitialArray(D，A［n］［m+1］)//根据事务数据库构造二维数组

4 算法实例

给出实例数据库如表1，设最小支持数为2.

1)首先扫描数据库将数据存入二维数组.函数 InitialArray(D，A［n］［m+1］) 对每个事务进行分解成单个项目存放在二维数组，A［n］［m+1］中(n为事务数，m为事务项数，m+1列统计总数)，如果该项存在，数组中用“1”表示，反之用“0”表示，结果如表2.

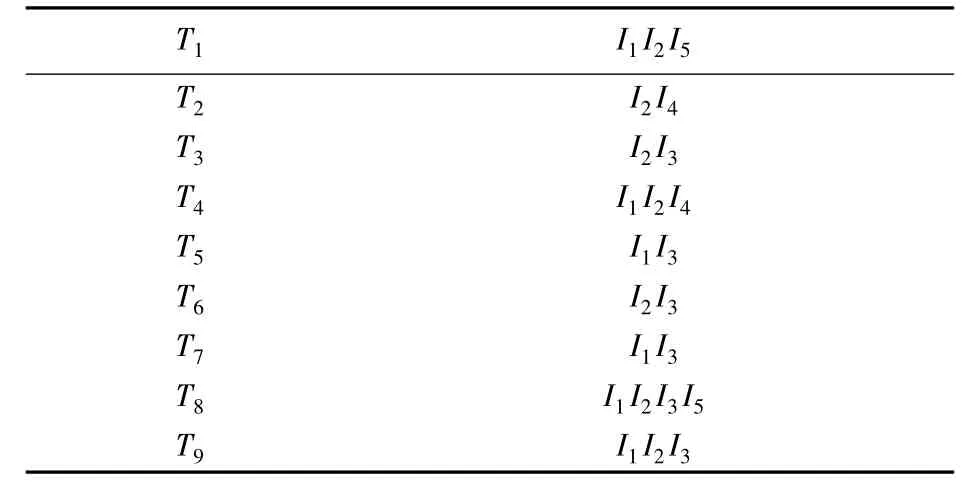
表1 实例数据库min_sup=2

存二维数组

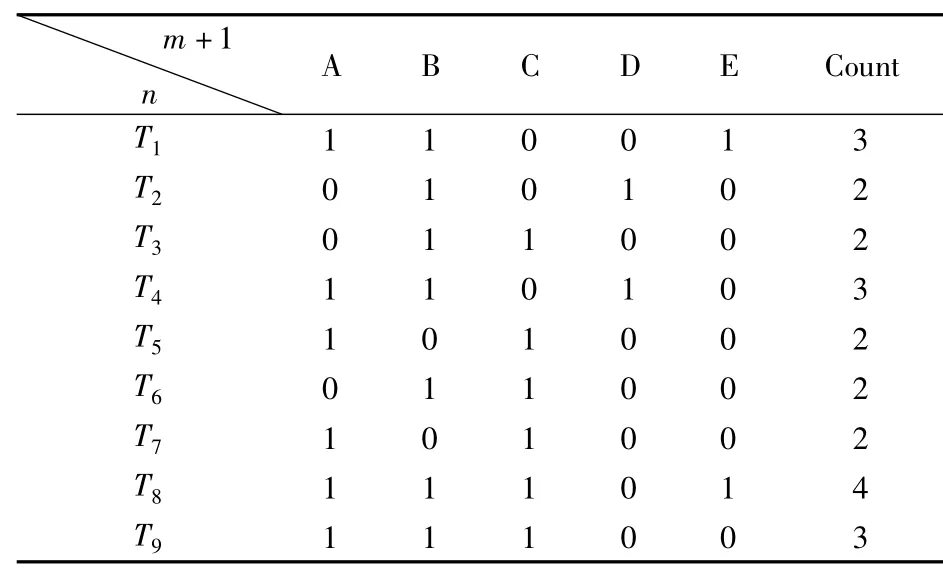
表2 二维数组对应表

2)根据频繁1－项集的获得函数

find_frequent_1_itemset(A［n］［m+1］)，对应二维数组中每列之和，即事务数据库中包含的每项的总数(如表3)，通过与min_sup比较，大于min_sup的各项就是要找的频繁1项集.表2的频繁1项集 是{I1，I2，I3，I4，I5}.

表3 数据库包含各项总数

3) 函数 apriori_gen(Lk－1，min_sup)根据频繁

k项集产生候选k项集.扫描相应的数组的列，统计每个候选项集的频度，如果数组中相应的列值均为1，则相应的计数值加1.由于篇幅限制，省略C2的产生过程，获得的频繁2项集是{I1I2，I1I3，I1I5，I2I3，I2I4，I2I5}.

3)统计L2中各项出现的次数(如表4)，其中I4的次数是1，所以I2I4不符合要求，删除此项，获得L'2(如表5).

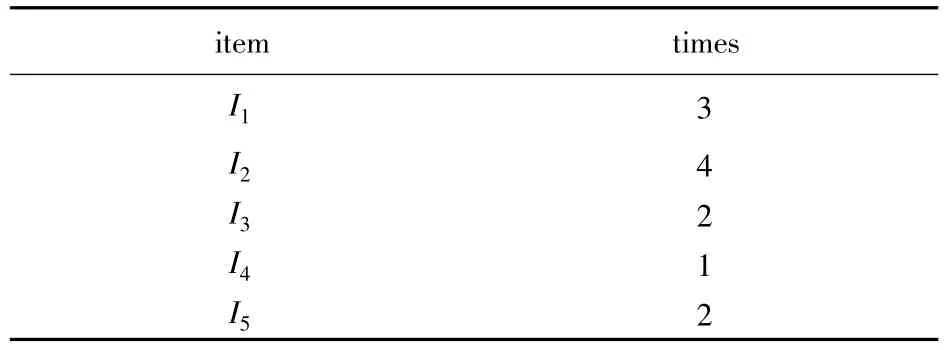
表4 各项次数统计

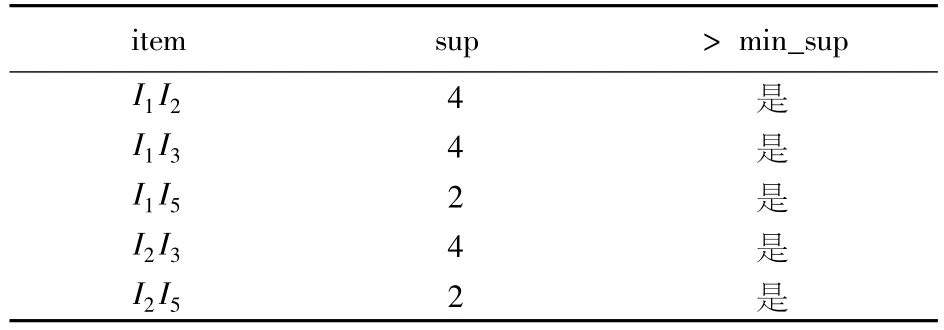
表5 符合要求的2项集

5)获得候选3项集(如表6).例如候选3项集{I1I3I5}，扫描数组中的I1I3I53列，只有在T8时3列同时是1，于min_sup=2.候选3项集{I1I2I3}，扫描数组中的I1I2I33列，T8，T9满足三列同时是1，计数为2，得出{I1I2I3}就是频繁3项集.频繁3项集(如表7).{I1I2I3}和{I1I2I5}的频繁计数是2，小于K+1=4(此时K是3)，算法结束，得到最大频繁3项集.

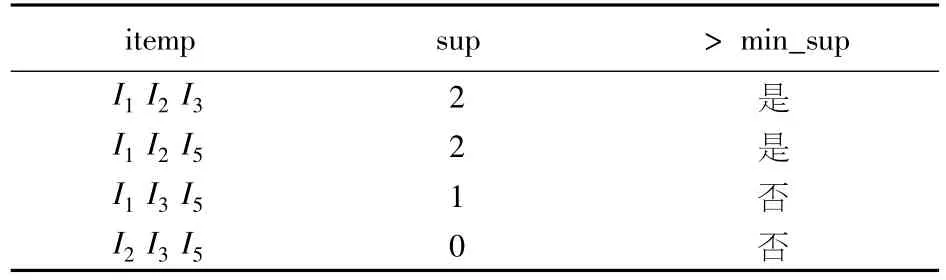
表6 候选3项集

表7 频繁3项集

5 结语

采用基于数组结构的方法对Apriori算法进行改进.该算法将事务数据库中项集信息存入二维数组中，用行表示事务信息，用列表式项信息.依行扫描相应的列来获得项集的频度，同时对频繁项集在进行自连接之前统计出所有项出现的次数，通过比较删除无用的项目集，提高了效率.但算法还有一定的局限性，数据库的规模影响到算法效率的提高程度.由于受到内存的限制，事务数据库中的数据可能不会一次性的全部存入数组，而用于关联规则挖掘的数据库通常是非常大的.

［1］邵峰晶，于忠清.数据挖掘—原理与算法［M］.北京:中国水利水电出版社，2003:36－43.

［2］张月琴.基于0－1矩阵的频繁项集挖掘算法研究［J］.计算机工程与设计，2009，30(20):4663－4664.

［3］杨妮妮.基于集合和位运算的频繁集挖掘优化算法［J］.科学技术与工程，2009，23(9):7173－7174.

［4］孟祥萍，钱 进，刘大有.基于数组的关联规则挖掘算法［J］.计算机工程，2003，29(15):98－99.

［5］刘 莹，郭福亮.基于数组的关联规则挖掘算法［J］.计算机与数字工程，2005，38(34):39－40.

［6］廖小平，王志坚，吴海玲.基于项编码的关联规则挖掘算法［J］.计算机与现代，2008(11):50－51.

［7］李 敏，刘 杰，Aprior算法的研究及在商业决策中的应用［J］.哈尔滨商业大学学报:自然科学版，2010，26(6):706－709.