太阳电池阵布局对微小卫星结构特性影响

郑 侃，廖文和，张 翔

（1.南京航空航天大学 机电学院，南京 210016；2.南京航空航天大学 高新技术研究院，南京 210016）

0 引言

近年来发射的航天器中，除了极少数以燃料电池、核能以及一次性化学电池组作为能源外，大多采用太阳电池阵和蓄电池联合供电的方式。太阳电池阵具有功率大、寿命长、重量小、构造简单可靠等一系列优点，非常适合作为微小卫星的空间电源[1-3]。太阳电池阵的构造形式各异，总的来说可分为体装式和展开式两大类[4-5]。

由于本文所涉及的微小卫星的功率消耗较小，因此采用体装式太阳电池阵和蓄电池联合供电的方式。所有的太阳电池均直接安装在六面体卫星的表面上。由于该微小卫星采用三轴稳定方式，因此对六面体上的太阳电池阵的设计有较高要求。从提高电能的角度希望尽可能增加侧板上电池片的数量，但电池片数量的增加又势必会减少侧板与骨架之间的固定连接件，这将会对整星的结构特性产生一定的影响，而且仅凭设计者的经验很难判断这种影响程度，故必须对其进行有效的理论分析和试验验证。

1 方案介绍

该微小卫星共有6块体装式太阳电池阵，并将其固定在侧板上。方案1为初始方案。方案2是在方案1的基础上减少了8个用于固定的M5螺钉，增加了侧板上太阳电池片的数量（如图1所示），从而可提高平均输出功率。该微小卫星有2块侧板安装了太阳敏感器，为方便说明，将其定义为太阳电池板B，其余4块定义为太阳电池板A。表1列出了两种方案的电性能参数。

图1 两种方案下太阳电池阵布局示意图Fig.1 Layouts of the solar cell array in two schemes

表1 两种方案的电性能参数对比Table 1 Comparison of electric performance parameters between two schemes

2 理论分析计算

2.1 有限元模型的建立

建立方案1的整星有限元模型。由于其主承力结构中采用了大量的铝蒙皮蜂窝夹层材料，而通常的有限元分析软件中没有与之对应的单元库，故采用三明治夹心理论进行等效处理。适配器是卫星与火箭的连接装置，其上下框为铝板结构，通过包带连接。由于包带具备一定的刚度和强度，因此用一个bush单元对适配器进行简化，其参数为试验值。适配器上下框采用四节点板单元，为了与整星结构的单元相协调，其单元大小与主承力结构板单元一致。另外，由主传力路径可知，无论是纵向还是横向激励，隔板和底板上载荷都较大，特别是在两者与适配器的连接处可能出现较强的应力集中现象，因此在建模过程中应尽量考虑节点单元的协调性。星上各单机均按集中质量处理，而电缆和接插件按非结构质量考虑。简化后的整星有限元模型如图2所示。

图2 整星力学分析有限元模型Fig.2 FEM model for the satellite

为了获得该微小卫星的响应特性，在方案1的基础上研制了结构星，并对其进行了有限元仿真分析和动力学试验。两种验证方式的结果均表明：在横向振动时，卫星的顶板部分测点的响应接近该板上设备的试验条件。以太阳敏感器为例，其附近的测点在y向正弦验收级试验条件下的加速度响应峰值达到了12.26g，接近该仪器y向加速度15g的试验条件。由于两种方案其结构阻尼的变化势必对顶板的响应以及整星的基频产生一定的影响，因此本文从结构响应灵敏度的角度分析了结构的阻尼对顶板太阳敏感器测点响应的影响程度。

2.2 卫星振动响应灵敏度分析计算

结构灵敏度分析是结构优化中的一项重要工作，它是利用泰勒展开式的一次或二次项估计质量、阻尼、刚度和设计变量的变化与模态参数以及响应之间的相关关系。由于本文所涉及的工程问题难以得到结构响应的表达式，因此该结构灵敏度的计算采用基于有限元技术的差分运算来代替微分运算[6-9]。简谐激励下的有阻尼强迫振动的运动方程为

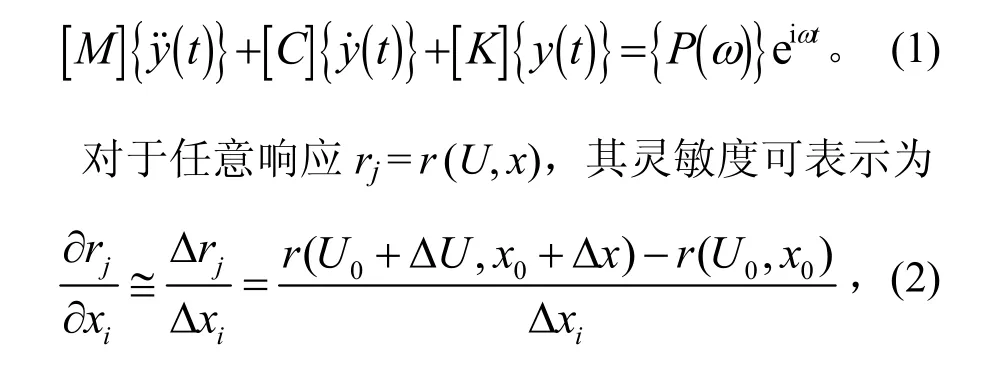
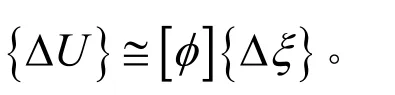
根据两个方案的特点，选取结构阻尼为变量并利用有限元分析软件对顶板太阳敏感器附近测点的响应灵敏度进行分析。方案1目标位置的最大响应灵敏度为-3.784 1×102g·m-1。

目标响应对整星结构阻尼的灵敏度的值为负，这说明随着整星结构阻尼的减小而顶板响应值逐步增大，同时该变量对目标函数的影响程度较大，达到了3.784 1×102。可以说两种太阳电池阵布片方式的不同所带来的阻尼变化势必对整星的结构特性产生较大的影响。对于本文所涉及的工程问题，两种方案结构阻尼变化的具体数值不能确定，因而不同于其他连续变量可以根据灵敏度分析的结果来修改结构参数以达到满足目标响应的要求。但通过灵敏度分析可以发现所选参数对目标响应的影响程度比较明显，因此必须在方案1分析的基础之上对方案 2进行补充振动试验以验证方案的可靠性及可行性。

3 试验验证

3.1 试验条件

为了验证阻尼变化对整星结构动力学特性的影响，对方案2进行了振动试验验证。试验条件与方案1完全一致[10]。正弦振动载荷为卫星发射时所有低频瞬态振动载荷的包络。而随机振动试验的频率范围一般在20～2 000 Hz，试验载荷量级一般用加速度功率谱密度与频率的关系曲线表示。本文主要关注正弦振动试验的结果，试验条件如表 2所示，而随机振动试验的条件在此不作介绍。

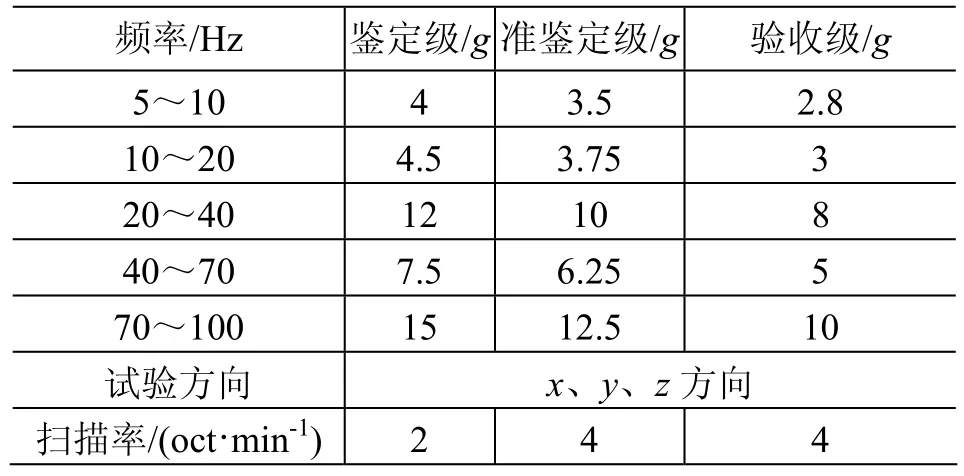
表2 验收和鉴定级正弦振动条件Table 2 The sinusoidal vibration test conditions for acceptance level and qualification level

3.2 试验结果对比分析

方案 2试验的响应测点位置的选定主要是参考了方案 1有限元分析模型及振动试验中顶板上响应较大的位置。试验选取了A1～A4号4个测点（对应方案1的23～26号测点），分别布置在顶板太阳敏感器和天线附近。两种方案的顶板各测点两次振动试验的结果的对比如图3所示。图4(a)、(b)分别为两种方案下顶板太阳敏感器附近测点在y向正弦验收级试验条件下的加速度响应曲线。

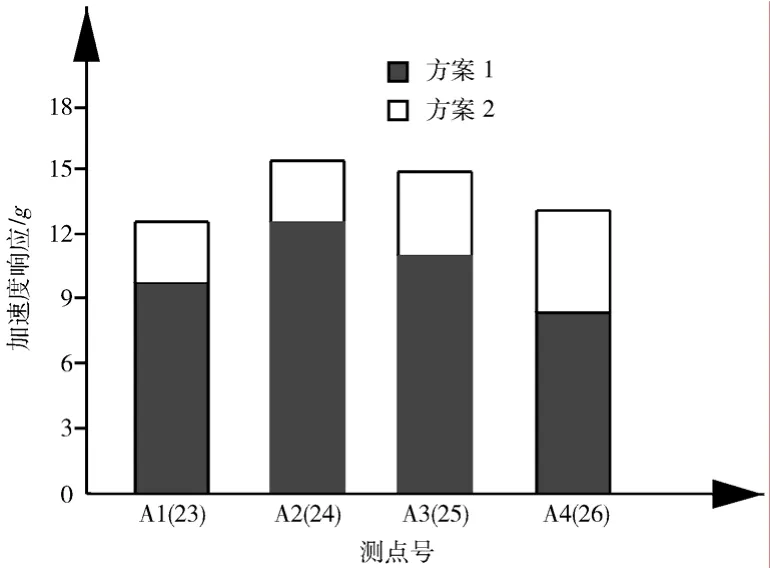
图3 两种方案下4个测点的加速度响应对比Fig.3 Comparison of the acceleration response for the four points in two schemes

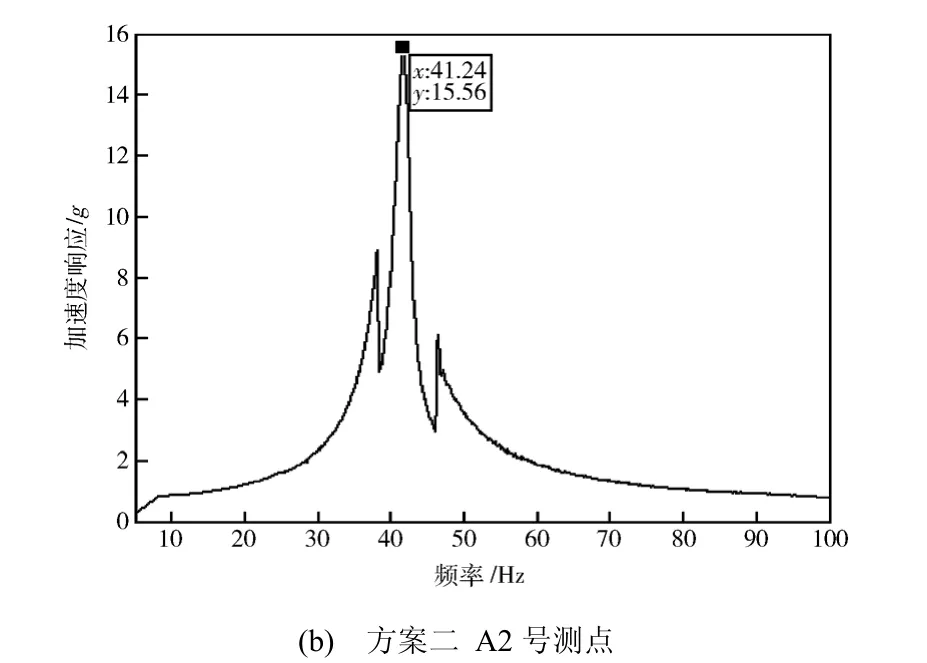
图4 两种方案下测点的y向加速度响应曲线Fig.4 Acceleration response curves for 24 testing point in scheme Ⅰand A2 testing point in scheme Ⅱ

通过对两种方案的测点的试验数据的采集和对比以及对试验现象的观察，得到以下结论：

1）方案1卫星的一阶频率分别为x向46.2 Hz，y向42.8 Hz，z向127.8 Hz；而方案2整星刚度略低，相比方案1降低了3.7%～8.2%，一阶频率分别为：x向42.4 Hz，y向41.2 Hz，z向117.5 Hz。两种方案的结构刚度均满足运载对该微小卫星的横向一阶频率大于25 Hz、纵向一阶频率大于35 Hz的要求。同时，所有连接螺钉和螺钉预埋件未出现断裂或脱落，满足强度要求。

2）方案2顶板太阳敏感器附近的A2号和A3号测点在y向正弦验收级试验条件下加速度峰值分别达到了15.58g和15.2g，特别是A2号测点的峰值相比方案1同位置测点提高了27.1%，同时也超出了太阳敏感器的加速度试验条件（15g）。顶板上的其他测点在正弦和随机试验条件下的加速度响应均在设备试验条件之内。

从以上两点可以得出，方案1结构的刚度优于方案2。虽然两者均满足运载提出的要求，但考虑到该微小卫星采用全蜂窝结构且蜂窝板的非线性振动会引起整星基频漂移的现象[11]，因此尽量选择刚度较大的方案。同时方案2顶板太阳敏感器附近的部分敏感测点的加速度响应相比方案 1有较大幅度提高，且超出了附近单机的试验条件，所以从结构特性的角度认为方案 1太阳电池阵的布局和连接方式的设计更为合理。

4 结束语

卫星的高可靠性要求其太阳电池阵布局必须建立在整星结构刚度和强度均得到保障的基础之上。本文通过地面力学环境试验对两种方案的整星结构特性进行了对比分析，认为方案1的设计更为合理。此研究所获取的整星顶板周边测点的结构响应可为今后体装式微小卫星太阳电池阵的布局设计提供参考。另外，考虑到所选方案中太阳电池片数量减少导致卫星功率降低3 W，因此必须调整星上某些设备的工作模式，并尽量提高星上蓄电池的供电能力，以保证该微小卫星在轨期间的正常工作。

（References）

[1]吕风格, 赵继广.微小卫星太阳电池阵的设计计算方法[J].装备指挥技术学院学报, 2005, 16(5)： 82-83

Lv Fengge, Zhao Jiguang.Research on design and calculation method of micro satellite solar array[J].Journal of the Academy of Equipment Command &Technology, 2005, 16(5)： 82-83

[2]Deluca A, Chirulli G.Solar array power conditioning for a spinning satellite[C]//ESA Communication.Noordwijk,Netherland, 2008： 7-8

[3]韩玉阁, 宣益民.卫星太阳能电池板热设计参数的灵敏度分析[J].南京理工大学学报： 自然科学版, 2006,30(2)： 178-181

Han Yuge, Xuan Yinmin.Parameter sensitivity analysis for the solar array of the satellite thermal design[J].Journal of Nanjing University of Science and Technology,2006, 30(2)： 178-181

[4]Nozaki Y, Yoshida T, Takahashi M.Design of solar array for ETS-VIII[C]//ESA, Noordwijk, 2002： 457-462

[5]陈烈民.航天器结构与机构[M].北京： 中国科学出版社, 2005： 355-360

[6]Wu Y T, Sitakanta M.Variable screening and ranking using sampling-based sensitivity measures[J].Reliability Engineering and System Safety, 2006, 91： 634-643

[7]Cacciola P, Colajanni P, Muscolino G.A modal approach for the evaluation of the response sensitivity of structural systems subjected to non-stationary random processes[J].Computer Methods in Applied Mechanics and Engineering, 2005, 194： 4344-4350

[8]侯悦民, 季林红, 金德闻.结构局部刚度变化对小卫星动特性影响[J].宇航学报, 2003, 24(6)： 588-592

Hou Yuemin, Ji Linhong, Jin Dewen.The effect of local stiffness of structure on dynamic characteristics of small satellites[J].Journal of Astronautics, 2003, 24(6)：588-592

[9]崔波, 杨新峰.卫星结构振动响应灵敏度分析[J].航天器环境工程, 2007, 24 (6)： 377-379

Cui Bo, Yang Xinfeng.Vibration response sensitivity analysis for satellite structures[J].Spacecraft Environment Engineering, 2007, 24(6)： 377-379

[10]郑侃, 廖文和, 张翔, 等.微小卫星动力学环境试验技术及其实验数据分析[J].航天器环境工程, 2010,27(3)： 328-331

Zheng Kan, Liao Wenhe, Zhang Xiang, et al.Dynamic environmental test technology and data analysis for micro-satellites[J].Spacecraft Environment Engineering,2010, 27(3)： 328-331

[11]陈昌亚, 宋汉文, 王德禹, 等.卫星振动试验中固有频率漂移现象初步研究[J].振动与冲击, 2003, 22(4)：23-25

Chen Changya, Song Hanwen, Wang Deyu, et al.Preliminary research on natural frequency drift in satellite vibration test[J].Journal of Vibration and Shock, 2003,22(4)： 23-25