多尺度椭圆形集料尺寸分布对混凝土边界效应的影响

许文祥 陈惠苏

(东南大学材料科学与工程学院，南京211189)(东南大学江苏省土木工程材料重点实验室，南京211189)

在细观水平上，混凝土可以看成是一种由集料和砂浆基体组成的二相复合材料［1］.因此，集料在混凝土结构中所占的体积分布从某种程度上决定了混凝土的力学性能和耐久性.依据体视学原理［2］，三维空间中的集料在混凝土内任一点的体密度可以用随机测试面截取混凝土获取集料的面密度表征，同时，在二维测试面内集料的面密度又可以用随机测试线段截取混凝土取得的集料线密度表征.因此，可以利用二维平面内集料的分布对混凝土边壁效应的影响来研究三维空间中集料分布的边界效应.

文献［3］首次利用实验的方法探讨了混凝土的边界效应，对混凝土进行切片压碎后分离出集料，然后测定集料在每个截面内的分布密度.混凝土由边壁层到内部中心，集料的体积分数先增加后逐渐稳定，界面过渡区厚度可能与混凝土边壁附近分布了很多粒径很小的集料有关.文献［4］通过实验手段并借助图像分析技术研究了混凝土边界效应层中粗集料的分布特征，集料的体积分数变化曲线为上升和水平两段，并定义界面过渡区厚度为粗集料的最小粒径.但在图像分析过程中，粗集料像素表征的界定存在很大的误差，截面尺寸过小导致数码照片中集料数目过少，因此，此方法存在一定的误差.文献［5］利用离散元算法模拟三维球形集料动态堆积的混凝土边界效应，得出集料体积分数随着混凝土边壁层向内部中心先上升，然后波动最后逐渐稳定的变化趋势.文献［6］借助于计算机模拟技术将集料模拟成二维圆盘，利用圆盘的有序随机分布模型研究了混凝土的边界效应，结果显示集料线密度随着边界距离的逐渐增大而先增大后减小最终趋于稳定的变化趋势，并且给出混凝土界面过渡区厚度为粗集料的最大粒径.文献［7］分析了不同形状和尺寸的单尺度椭圆形集料对混凝土边界效应的影响，结果显示界面过渡区厚度与椭圆形集料的长轴和等效直径有关.但是，该研究基于固定的集料面积分数，并未考虑集料的面积分数对混凝土界面效应的影响.

本文利用计算机模拟多尺度椭圆形集料的等体积分数分布对混凝土边界效应的影响，根据等体积分数分布，将多尺度椭圆形集料有序随机分布在一个二维平面内;根据多尺度椭圆形集料的等体积分数分布分析混凝土的边界效应;最后，给出椭圆形集料在混凝土中分布规律.

1 随机堆积模拟

假定集料粒子的形状为椭圆形，相对于圆形和球形，椭圆形粒子更能表征集料的真实形状.由于混凝土在成型过程中会出现边界效应，集料粒子在混凝土边壁层附近的分布呈现特殊的规律［8］.为了研究这种规律，利用计算机模拟多尺度椭圆形集料在二维平面内有序随机分布，并借助体视学中线密度的定义表征椭圆形集料在混凝土边壁层附近的分布规律.椭圆形集料分布在一个矩形容器内，为了尽量减小矩形容器对多尺度椭圆形集料分布的影响，设置矩形长l=5 m，宽h=1 m.矩形容器的上下边壁为刚性边界条件，左右边壁为周期性边界条件［9］.

尽管在混凝土试件中集料的级配受到很多因素的影响，如粒子间的位置情况［10］以及密实度等［11］.但是，在计算机模拟中，混凝土集料粒子分布通常采用一定的集料级配来表征，如Fuller级配和等体积分数级配等［6，12］.本文采用等体积分数级配，因为等体积分数级配得到的集料粒子数量最多，模拟混凝土结构的密实度很高［6］.设置椭圆形集料粒子的长轴为a，短轴为b，在椭圆形集料粒子的级配过程中，椭圆形粒子的长径比α=b/a保持恒定.根据体视学理论［6］，等体积分数级配的累积面积基概率密度函数为(见图1)

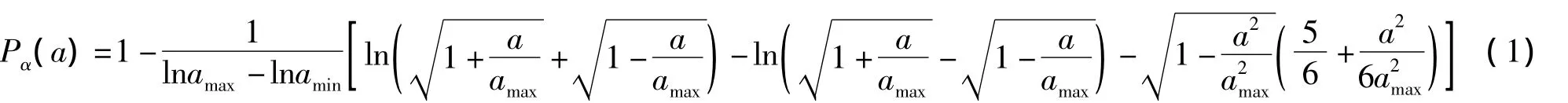
式中，amax，amin分别为椭圆形集料粒子的最大和最小长轴(粒径).由图1可以获取与椭圆长轴对应的累计面积基概率密度函数值，由体视学理论，可求出在不同长轴a下的椭圆形集料粒子数量.

多尺度椭圆形集料分布原则是保证每个椭圆形粒子之间互相不重叠，因此，判断椭圆重叠的算法对于研究多尺度椭圆形集料分布的混凝土边界效应的计算机模拟是至关重要的.本文采用判断椭圆之间重叠的数值算法进行集料粒子的有序随机分布模拟［13］.由于实际混凝土中集料的体积分数Vs高达60% ～80%［14］，在多尺度椭圆形集料分布的计算机模拟中，可以预先设置集料的面积分数Aa为 0.60 ～ 0.80.图2 显示了 Aa分别为 0.60，0.65，0.70，0.75 的多尺度椭圆形集料粒子在半周期边界的矩形容器内随机堆积计算机模拟示意图.从图2中可以看出，没有任何一个椭圆形集料粒子互相重叠.

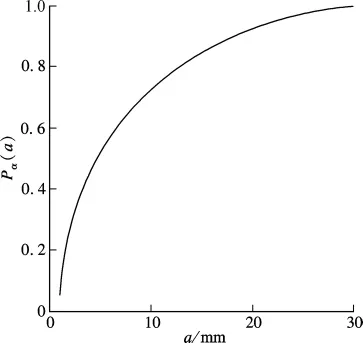
图1 累计面积基概率密度Pα(a)与椭圆长轴a的关系

图2 多尺度椭圆形集料粒子有序随机分布模拟示意图

2 集料分布对混凝土边界效应的影响

依据体视学原理［2］，Vs=Aa=LL.因此，二维平面内集料边界效应的结果同样可以代表三维空间中集料分布的边界效应.在二维的情况下，为了研究粒子形状对边界效应的影响，采用体视学的线采样规则，即

式中，L为平行于矩形容器的刚性边壁长度(见图3);Le为测试线段L在距离刚性边壁y处被矩形容器内的椭圆所截取的线段长度总和.

图3 线采样表征示意图

由于混凝土中任一点的集料固相体积分数是y的函数，所以随着测试线段L从矩形边壁向矩形内部每次移动距离y时，都可以获取一个集料固相体积分数.对于给定的混凝土集料面积分数Aa，利用计算机模拟n次多尺度椭圆形集料的有序随机分布，就可以得到相应的统计特性.因此，可以用n次椭圆形集料分布的平均固相体积分数来表示.为了节省计算机模拟所耗费的时间以及结果的统计可靠性，针对等体积分数级配，用单尺度椭圆形集料模拟结果［7］，设定n=100次模拟后的平均统计结果作为多尺度椭圆形集料尺寸分布对混凝土边界效应影响的参考值.

2.1 最大粒径对混凝土边界效应的影响

文献［6，13］阐述了二维圆盘形集料分布的界面过渡区厚度与圆盘的最大粒径有关;文献［3］借助图像分析技术得出混凝土界面过渡区厚度应等于粗集料的最小粒径.鉴于此，本文在集料面积分数一定的条件下，保持椭圆粒子长径比α=0.7，最小粒径amin=5 mm.

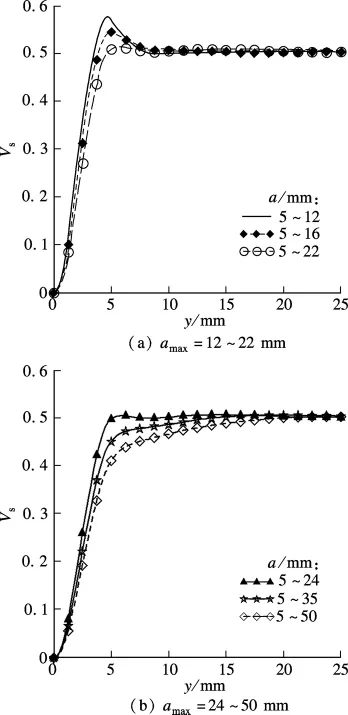
图4 不同最大粒径的椭圆形集料固相体积分数曲线

图4为多尺度椭圆形集料最大粒径由12 mm增加到50 mm时混凝土结构中固相体积分数Vs随距离y的变化曲线.可以看出，多尺度椭圆形集料最大粒径的变化改变Vs随y变化的曲线形状.当多尺度椭圆形集料粒径范围从5～12 mm等体积粒径分布时，混凝土结构中的固相体积分数曲线分为上升、下降、再上升，最后趋于稳定的4段(见图4(a))，与单尺度椭圆形集料对混凝土边界效应影响的曲线形状一致［7］.然而，当多尺度椭圆形集料粒径范围为5～16 mm和5～22 mm等体积粒径分布时，混凝土结构中的固相体积分数曲线形状变为上升、下降，然后趋于稳定的3段，与文献［6］中圆盘形集料粒径范围在5～16 mm内的固相体积分数曲线形状一致.从图4(b)可以看出，当椭圆形集料的最大粒径从24 mm继续增大时，混凝土结构中固相体积分数曲线形状变化为先上升后稳定的2段，而且随着粒径范围的不断增大，固相体积分数曲线变得更加平滑，与文献［1］的实验结果一致.因此，在计算机模拟混凝土边界效应时，应选取合适的集料粒径范围才能真实地模拟试验环境.

从图4中可以看出，混凝土结构中固相体积分数Vs曲线稳定时的值都约等于混凝土结构中集料的面积分数Aa.图4(a)显示了固相体积分数曲线的最高峰值点对应的距离y随着最大粒径的增大都约等于最小粒径.但是，最高峰值却不断地下降，当最大粒径从12 mm增加到22 mm时，最高峰值却成0.58降低到0.51.然而，当最大粒径继续增大时，最高峰值点随即消失(见4(b)).同时，随着多尺度椭圆形集料最大粒径的变化混凝土结构成型过程中模板与集料间的界面过渡区厚度［7］也发生了相应地变化(见图5).当最大粒径从12 mm增加到22 mm时，界面过渡区厚度与最大粒径amax呈现良好的正相关关系(见图5(a))，线性回归方程为

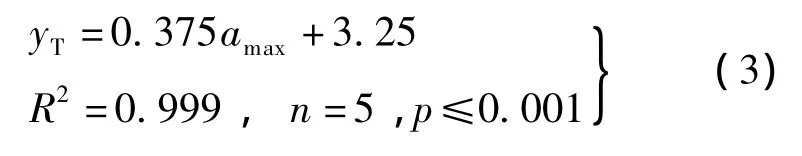
式中，yT为界面过渡区厚度.由式(3)可知，当多尺度椭圆形集料的最大粒径增大时，界面过渡区厚度呈线性增长.图5(b)显示了最大粒径从24 mm增加到50 mm时的界面过渡区厚度变化曲线，同样可以看出，最大粒径和界面过渡区厚度呈现良好正相关关系，线性回归方程为

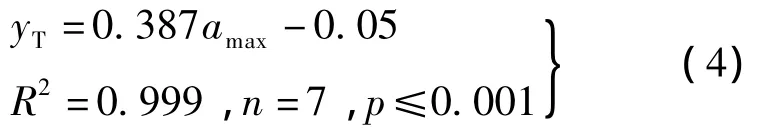
由式(3)和(4)可知，多尺度椭圆形集料的尺寸分布所产生的界面过渡区厚度随集料粒子的最大粒径增长而线性增大，并非定值，与文献［4］中界面过渡区厚度为定值(约等于粗集料的最小粒径)以及文献［6］中界面过渡区厚度等于集料最大粒径的结论不相符.其原因可能是文献［4］所选取的集料粒径范围为5～30 mm，用像素点表征集料尺寸存在一定误差，并未做过相应的对照试验.文献［6］选取圆盘形集料粒径范围在5～16 mm内过于狭小，而且也未做过相应的对照模拟试验.

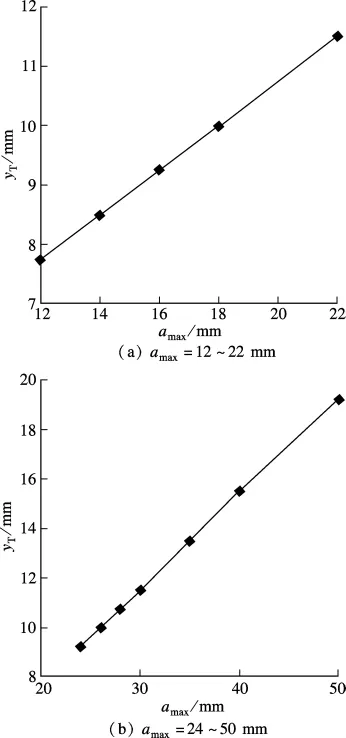
图5 不同的最大粒径的界面过渡区厚度变化曲线

2.2 集料面积分数对混凝土边界效应的影响

不同集料面积分数对二维圆盘形集料分布的边界效应没有显著性的影响，在不同的面积分数下，圆盘的分布密度变化趋势都一致，先增大后减小，最终趋于稳定［15］.然而，不同的集料面积分数对多尺度椭圆形集料分布边界效应的影响目前还尚未报道.因此，本文设置混凝土中多尺度椭圆形集料的尺寸范围为1～30 mm，面积分数Aa分别为0.40，0.45，0.50，根据以上模拟结果，可得出在不同的面积分数下多尺度椭圆形集料分布边界效应的影响(见图6).

从图6中可以看出，虽然混凝土中设置的Aa不同，Vs随y的变化曲线形状十分相似，均由平滑的上升和趋向稳定两部分组成，Vs达到稳定时的值都对应于各自的Aa.随着Vs的改变，混凝土成型过程中模板与集料之间的界面过渡区厚度［7］也发生相应的变化.当Aa增大时，混凝土的界面过渡区厚度随之减小，其原因可能是集料的面积分数增大，提高了混凝土的密实度，从而降低了混凝土的边界效应.利用多尺度椭圆形集料对混凝土边界效应的模拟比圆盘形集料模拟的结果更接近于文献［3-4］中的实验结果，主要是因为多尺度椭圆形集料形状更接近于集料的真实形状.因此，利用多尺度椭圆形集料分布对混凝土边界效应影响的模拟更具有代表性和真实性.

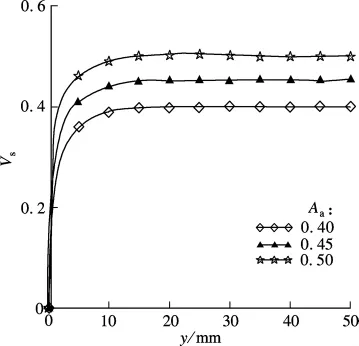
图6 不同的面积分数的集料固相体积分数曲线

3 椭圆形集料平均分布密度的分布规律

根据不同集料面积分数下的模拟结果，运用数学拟合的方法求出椭圆形集料在混凝土中分布的固相体积分数的表达式，即

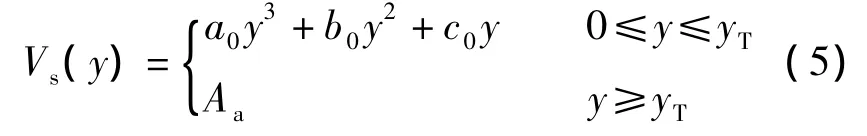
式中，a0，b0，c0为待定系数，已知

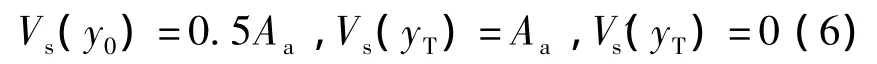
式中，y0为集料固相体积分数达到面积分数一半时的距离.联立式(5)和(6)，可求出待定系数a0，b0，c0，即

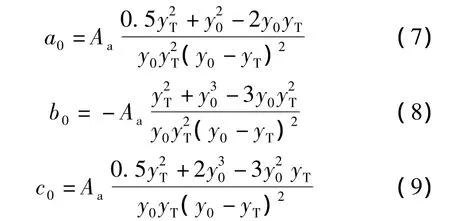
由式(7)、(8)和(9)可以看出，待定系数 a0，b0，c0都是关于集料面积分数Aa的变量.根据模拟所得数据进行拟合，可得混凝土界面过渡区厚度为

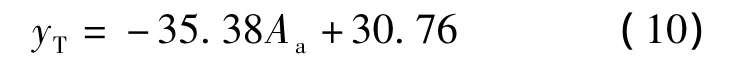
联立式(5)～(10)可得集料的固相体积分数.由式(10)也可以看出，界面过渡区厚度yT随集料的面积分数Aa的增大而降低.当混凝土集料的面积分数从0.4增大到0.5时，界面过渡区厚度由18 mm降低到10 mm.

4 结论

通过计算机模拟多尺度椭圆形集料尺寸分布对混凝土边界效应的影响，借助体视学中线采样的方法，探讨了多尺度椭圆形集料尺寸在等体积分数级配下的分布规律.通过模拟和分析，首先得出多尺度椭圆形集料的固相体积分数曲线形状随着集料最大粒径的增大从先上升后下降，再上升最后趋于稳定的4段变化为先上升后下降再趋于稳定的3段，直至演变为先上升后稳定的2段，稳定后的固相体积分数都等于集料的面积分数.而且，随着最大粒径的增大，界面过渡区厚度并不是一个定值，而是随着最大粒径的增大而线性增长.因此，在计算机模拟混凝土边界效应时，应选取合适的集料粒径范围才能真实地模拟实验环境.在保证合适的集料粒径范围的前提下，随着集料面积分数的增大，界面过渡区厚度逐渐降低，但是，在不同的集料面积分数下，多尺度集料的固相体积分数变化趋势都为上升和稳定两段曲线.基于这些模拟的结果，本文给出了集料固相体积分数的数学拟合表达式，分析得出利用多尺度椭圆形集料有序随机分布的模拟研究混凝土的边界效应更具有真实性和代表性.

References)

［1］Zheng J J.Mesostructure of concrete-stereological analysis and some mechanical implications［D］.Delft，the Nederlands:Department of Civil Engineering and Geosciences，Delft University of Technology，2000.

［2］Russ J C，Dehoff R T.Practical stereology［M］.2nd ed.New York:Plenum Press，1999.

［3］Kreijger P C.The skin of concrete composition and properties［J］.Materials and Structures，1984，17(100):275-283.

［4］杨进波，阎培渝.混凝土边界效应层中粗骨料的分布特征［J］.建筑材料学报，2009，12(5):580-583.Yang Jinbo，Yan Peiyu.Distribution characteristics of coarse aggregate in wall-affecting layer of concrete［J］.Journal of Building Materials，2009，12(5):580-583.(in Chinese)

［5］Stroeven M.Discrete numerical modelling of composites materials［D］.Delft，the Nederlands:Department of Civil Engineering and Geosciences，Delft University of Technology，1999.

［6］Zheng J J，Li C Q，Zhao L Y.Simulation of two-dimensional aggregate distribution with wall effect［J］.ASCE Journal of Materials in Civil Engineering，2003，15(5):506-510.

［7］Xu W X，Chen H S，Lü Z.An overlapping detection algorithm for random sequential packing of elliptical particles［J］.Physica A:Statistical Mechanics and its Applications，2011，390(13):2452-2467.

［8］Chen H，Sun W，Stroeven P，et al.Analytical solution of the nearest surface spacing between neighboring aggregate grains in cementitious composites［J］.Journal of theChineseCeramicSociety， 2005， 33(7):859-863.

［9］Xu W X，Chen H S.A numerical algorithm for detecting inter-ellipse particles overlapping［C］//Proceedings of The First International Conference on Advances in Interaction ＆ Multiscale Mechanics.Seoul，2010:1358-1371.

［10］陈惠苏，孙伟，Stroeven P，等.混凝土中邻近集料表面最近间距分布的计算机模拟［J］.硅酸盐学报，2004，32(4):429-435.Chen Huisu，Sun Wei，Stroeven P，et al.Computer simulation of the nearest surface distance distribution between neighbor aggregate grains in concrete ［J］.Journal of the Chinese Ceramic Society，2004，32(4):429-435.(in Chinese)

［11］Neville A M.Properties of concrete［M］.4th ed.New York:John Wiley ＆Sons，1995.

［12］Zheng J J，Li C Q.Three-dimensional aggregate density in concrete with wall effect［J］.ACI Materials Journal，2002，99(6):568-575.

［13］Xu W X，Chen H S，Lü Z.A 2D elliptical model of random packing for aggregates in concrete［J］.Journal of Wuhan University of Technology:Materials Science Edition，2010，25(4):717-720.

［14］Nawy E G.Fundamentals of high performance concrete［M］.2nd ed.New York:John Wiley ＆Sons，2001.

［15］赵良颖，郑建军，周欣竹，等.二维骨料分布边界效应的计算机模拟［J］.建筑材料学报，2003，6(3):301-307.Zhao Liangying，Zheng Jianjun，Zhou Xinzhu，et al.Computer simulation of two-dimensional aggregate distribution with wall effect［J］.Journal of Building Materials，2003，6(3):301-307.(in Chinese)