饱和状态下水泥浆体的微观结构冰冻损伤模型

刘 琳 孙 伟 陈惠苏 叶 光 钱智炜

(1东南大学材料科学与工程学院，南京211189)(2东南大学江苏省土木工程材料重点实验室，南京211189)(3荷兰代尔夫特理工大学土木与地球科学学院微观材料实验室，Delft 2628CN)

水泥基复合材料在受到冰冻(或冻融循环)作用后性能的劣化是关系到寒冷地区混凝土结构耐久性和服役寿命的重要因素之一.混凝土的抗冻性和冻结破坏的机理在过去几十年中一直是一个热点问题，许多学者先后提出了不同的混凝土冰冻破坏机理.主要有静水压和渗透压理论学说［1］、冰的结晶压理论学说［2-3］和微冰透镜理论学说［4］.虽然对冰冻引起的混凝土破坏机理有不同的理解，但最根本原因是液态水转变为冰晶体时产生了9%的体积膨胀.而混凝土受冻破坏后的各种性能变化(如弹性模量降低、强度下降、传输性能增加及质量损失等)，都是由材料本身微观结构劣化造成的.而引起这个微观结构劣化的重要原因之一，正是水与冰在其内部孔隙中发生相变并伴随体积变化造成的.

为了深入理解在冰冻作用时水泥基复合材料的孔隙中的水分发生相变带来的危害和材料内部微观结构的损伤过程，本文建立了一个饱水状态下水泥浆体的冰冻破坏模型.从水泥浆体的微观结构出发，抓住冰在孔隙中的成核与生长过程，将水由液态转变为固态时的体积膨胀转换为力学因素，分析水泥浆体微观结构内部的受力及分布，量化水泥浆体的内部损伤，从而建立一个水泥浆体微观结构劣化的数值模型.

1 破坏机理

在温度降低过程中，冰晶体首先在大孔中形成，然后随温度继续降低，大孔中的冰向小孔中生长［2-3］.在不同温度条件下，可形成冰的最小孔半径［2］，即

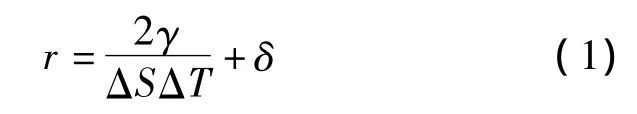
式中，ΔT为从冰点到当前温度的温度差，ΔT=Tm-T，Tm为大块冰的冰点，T为当前温度，K;δ为冰与孔壁之间的水膜厚度，μm;γ为冰与水之间的界面能，J/m2;ΔS为每单位体积冰溶解为水的熵，MPa/K.

当含水材料受冻时，微观结构的破坏机理主要与孔的大小有关.当温度低于冰点时，较大毛细孔中的水首先转变为冰发生体积膨胀，而孔隙周围的固相抑制孔内物质的膨胀，使得孔隙周围的固相承受一定的应力(见图1).固相中每点处的应力的大小和方向与该点所在的位置到达孔的距离、孔的形状、固相和冰的弹性模量、剪切模量、抗拉强度等因素有关.当固相所承受的局部拉应力大于其局部抗拉强度时，即产生微裂缝.当温度继续降低时，冰在更小的孔隙中生长(见图2).根据结晶压理论，小孔中的冰受到来自孔壁的压力［2，5］，即

式中，κE，κM分别为冰的自由端和冰与孔壁接触处曲率.在孔壁施加给冰一定作用力的同时，也受到来自冰的大小相等方向相反的作用力.

文献［5］模拟了随着温度降低，由冰的结晶压引起的水泥浆体微观结构的破坏过程.本文研究在较大孔径中由水转变为冰时体积膨胀所引起的水泥浆体的微观结构损伤.对于饱水状态的水泥浆体，由于其内部微观结构的复杂性，表现为孔隙大小不一、形状变化多样、固相的构成组分多样(未水化水泥颗粒和各种水化产物)等，因此，很难仅使用图1所示的概念模型反映真实的微观结构破坏.本文试图建立能够量化微观结构破坏，从本质上把握由水转变为冰的体积膨胀所带来的微观结构损伤的结构模型.

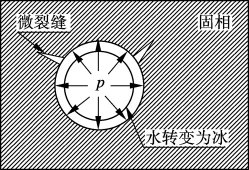
图1 由膨胀性产物引起的破坏机理示意图

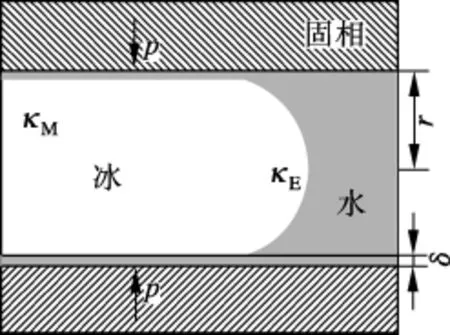
图2 冰在小孔中的结晶［5］

2 模型的建立

在水泥浆体低温受冻过程中，当温度低于冰点时，冰首先在受冻表面的孔中形成，然后冰晶体在微观结构内部的含水孔隙中生长.由于孔中的水分由液态转变为固态时产生9%的体积膨胀，使得水泥浆体内部承受一定的应力，这个内应力使得水泥浆体产生了内损伤.水泥浆体微观结构的冰冻破坏过程模拟流程图如图3所示.

首先，将冰冻过程中的连续温度变化离散为一系列的小温度区间(ΔTk，k=1，2，…，n)，每2 个相邻温度区间之间具有一定的温度差;由水泥浆体的微观结构得到其孔结构信息，分析处于不同温度区间时水泥浆体孔隙中的液态水与结晶态冰的转化过程，即冰的成核与生长过程.在得到冰晶体在孔隙中的三维分布后，把受冻后的水泥浆体微观结构转变为三维格构结构.最后，把这个冰冻后的水泥浆体三维格构结构作为研究对象，计算水泥浆体中的内应力大小及分布.当局部区域固相所承受的内应力大于其抗拉强度时，格构结构发生局部断裂，表现为微裂缝，水泥浆体内部发生损伤.

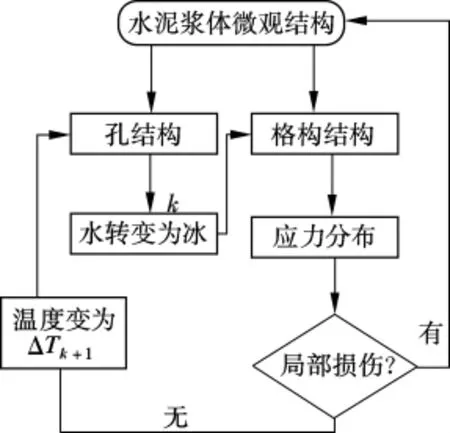
图3 模拟水泥浆体微观结构冰冻破坏流程图

2.1 水泥浆体模拟结构

由图3可知，在模拟水泥浆体微观结构的受冻破坏过程中，首先需要通过实验或计算机模拟得到水泥浆体的微观结构.由Micro-CT［6］、聚焦离子束［7］等实验手段得到的水泥浆体微观结构虽然可靠性较高，但往往受到分辨率的限制，且比难操作.目前世界上模拟水泥浆体微观结构的计算机模型主要有 HYMOSTRUC3D［8-10］，CEMHYD3D［11］和Mic［12］等.本文借助 HYMOSTRUC3D 模型得到水泥浆体的模拟微观结构.

HYMOSTRUC3D模型假设所有水泥颗粒为球形，在水泥水化过程中，生成水化硅酸钙和氢氧化钙2种水化产物，其中氢氧化钙被转变为等体积的水化硅酸钙产物包裹于未水化水泥颗粒外部.包裹于未水化水泥颗粒外部的水化产物又分为内部水化产物和外部水化产物2种.水泥浆体的水化程度是水泥粒径分布、化学组分、水灰比、反应温度以及时间的函数［8-10］.

本文用HYMOSTRUC3D模型模拟水灰比为0.4的普通波特兰水泥(型号42.5N)水化至一定程度的微观结构.水泥所含主要矿物成分为C3S(64%)，C2S(13%)，C3A(8%)和 C4AF(9%)，表观细度为420 m2/kg.模拟试样尺寸为100 μm×100 μm ×100 μm，水泥最小粒径为 1 μm.将水泥浆体的模拟微观结构用三维像素形式表示出来，在分辨率为 0.5 μm/像素的条件下，水化程度为0.69的水泥浆体微观结构如图4所示.考虑现有计算机的计算能力，本文采用边长为25 μm模拟结构(见图4)，是从所生成的边长为100 μm的模拟结构中截取而来.每个像素用不同的数值表示，0，1，2，3分别表示孔相、未水化水泥颗粒相、内部水化产物相和外部水化产物相.模拟微观结构中的孔相是指充满水的毛细孔.水泥浆体在低温受冻时，冰的产生与生长就是发生在这些充满水的毛细孔中.图4所示模拟微观结构中的孔结构如图5所示.

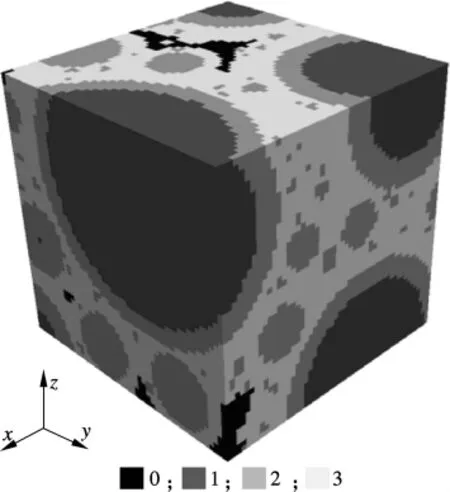
图4 水泥浆体模拟微观结构图

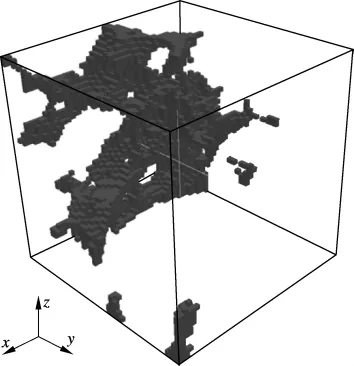
图5 水泥浆体模拟孔结构图

2.2 冰在孔结构中的生长

由式(1)可知，在温度降低过程中，冰晶体首先在大孔中形成，随着温度的降低，大孔中的冰晶体向小孔中生长［2-3］.当 ΔT=0.27 ℃时，在直径为0.5 μm的孔中有冰生成.本文假设水泥浆体沿x轴方向左边表面为受冻面，冰晶体首先在这个表面上的孔中生成，然后向孔隙内部生长.由于是在微观层次研究冰的生长，因此不考虑温度梯度的影响.用燃烧算法［13］来模拟冰的内部生长过程.模拟所得到的温度等于冰点时水泥浆体的模拟孔结构(见图6).此时，与受冻面上冰连通的孔隙中的水全部变为冰，而不连通的孔隙中的水仍然保持液态.图6所示孔结构的体积占整个微观结构总体积的4.7%(因所截取的微观结构的大小不同而有所变化)，孔隙中有97.6%的水转变为冰.在得到孔中水和冰的分布信息后，根据含有液态水、晶体态冰和固相水化产物(包括未水化水泥颗粒、内部和外部水化产物)的水泥浆体微观结构生成与之相对应的格构结构，并运用格构结构断裂模型分析微裂缝的产生.

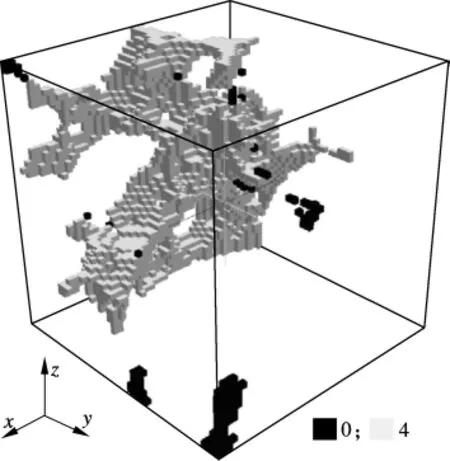
图6 冰冻后水泥浆体模拟孔结构图

2.3 水泥浆体三维格构结构断裂模型

格构结构由一系列格构单元(lattice element)组成，每个单元均能承受一定的力学荷载.格构结构断裂模型在水泥基复合材料领域得到广泛应用，如预测水泥浆体在微观尺度的力学性能［14-15］、分析混凝土的受力破坏［16］等.本文使用该模型预测水泥浆体在冰冻作用下的局部断裂.水泥浆体格构结构的断裂模型可以分为以下几个步骤实现:①格构结构的生成;② 格构单元力学性能的确定;③格构单元受力分析及断裂过程.

2.3.1 格构结构的生成

文献［15］详细介绍了四角形格构结构的建立方法.以二维情况为例，如图7(a)所示，首先生成一个方格网络(grid)，每个方格网表示为一个元件(cell).元件中含有子元件(sub-cell)，子元件与元件边长的比值定义为随机度(randomness).随机度的取值在0～1之间，随机度表示材料微观结构的无序程度，若随机度为0，对应的材料是理想均匀材料，随机度为1，对应的材料是完全无序的非均质材料.定义好所有元件与子元件后，在子元件中随机生成一个节点(node)，相邻2个节点则构成一个格构单元 (lattice element).假如元件所在的位置是孔相，则不在此元件中生成节点.这样所生成的格构结构能够反映材料的力学性能［15］.然而，在含有冰晶体的水泥浆体中，冰的生成不但产生体积膨胀，而且会承受一定的应力.因此，不能仅将水泥浆体中的固相水化产物(包括未水化水泥颗粒、内部和外部水化产物)作为基本元件来建立格构结构，而需要将冰冻过程中形成的冰晶体作为新的元件引入结构中，这样新的节点和格构单元随之产生.如图7(b)所示，在冰相的元件上需要生成新的节点.由于冰晶体与水泥浆体中的固相水化产物的性质有很大不同，因此并不能简单地连接冰节点与固相节点形成新的格构单元.要在冰与固相的连接处再插入一个新的节点形成2个格构单元，一个格构单元具有冰的性质，另一个格构单元具有固相水化产物的性质.根据上述四边形格构结构的建立方法，一个模拟水泥浆体的三维格构结构如图8所示.图8中随机度为0的格构单元表示在已结冰的孔隙中形成的冰单元，随机度为1的格构单元表示由固相水化产物构成的单元.在此情况下，共有36.1万个固相水化产物梁单元和1.4万个冰晶体梁单元生成.

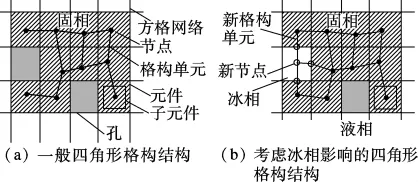
图7 四角形格构结构生成示意图

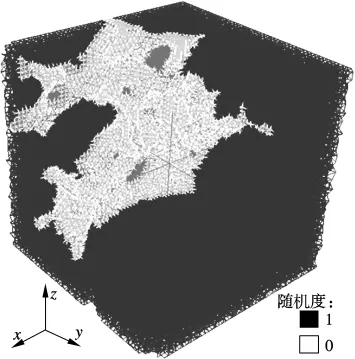
图8 由冰晶体和固相水化产物组成的水泥浆体格构结构

2.3.2 格构单元性能的确定

水泥浆体格构结构的基本组成单元是由冰或者水泥水化产物组成的格构单元，这些单元具有各自的形状参数、弹性模量、剪切模量和抗拉强度.本文假设所有格构单元都是圆柱形梁单元，单元长度等于2个节点之间的距离，横截面面积等于垂直于长度方向的表面面积［17］.图8所示格构结构中每个梁单元的横截面面积取值为0.25 μm2.据表1所列的四相节点，格构结构的梁单元共可分为7种类型，每种类型由其两端的格构节点的相(相1和相2)共同决定(见表2).表3列出了这7种类型的格构单元的力学性能.由冰晶体组成的梁单元不会受到拉应力的作用(类型7)，因此未考虑其抗拉强度.假如冰晶体不受到压应力作用，其与周围固相表面相接触的节点即会与固相分离，冰晶体进入自由伸缩状态.

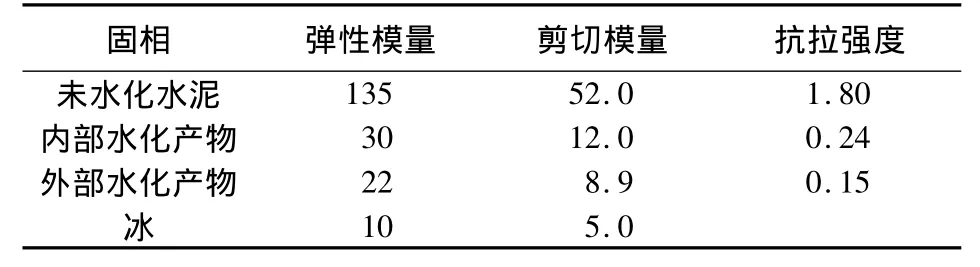
表1 梁单元的力学性能［18-21］ GPa

表2 格构单元组分类型

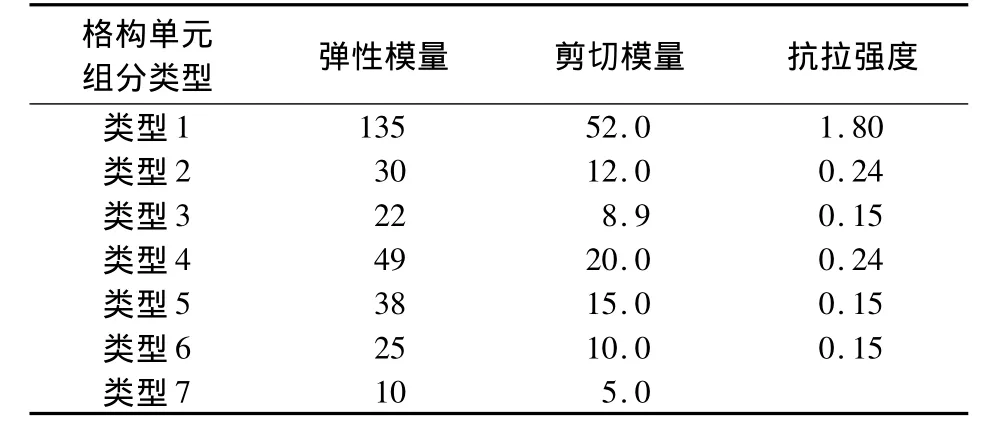
表3 格构单元的力学性能［18-21］ GPa

2.3.3 格构单元受力分析及断裂过程

由于本文所考虑的内应力主要来源于水转变为冰时所产生的体积膨胀，在格构结构中表现为冰晶体梁单元的长度变化，为相变之前的03倍.由冰组成的梁单元长度的伸长，使与之相衔接的其他类型的梁(类型1～类型6)受到不同程度的挤压或拉伸，从而产生了内应力.由于水泥浆体微观结构的复杂性，梁单元的分布错综复杂，从而使部分梁单元承受拉应力，部分承受压应力.假设梁单元只会受拉破坏，承受拉应力的梁单元在其所受应力大于其抗拉强度时(见表3)，该梁单元断裂.在水泥浆体不受到外部强加荷载的条件下，格构结构的边界条件设定为自由膨胀.

3 模拟结果

在所截取的水灰比0.4、水化程度0.69、边长25 μm的水泥浆体微观结构中，孔隙率为4.7%.当受到冰冻作用温度ΔT=0.27℃时，孔隙中有97.6%的水转变为冰.由水转变为冰所带来的体积膨胀，致使水泥浆体的三维格构结构中的部分梁单元断裂.通过对具有36.1万个固相水化产物梁单元和1.4万个冰晶体梁单元的格构结构受力分析发现，有275个梁单元断裂，在梁单元断裂位置产生微裂缝;微裂缝的形状表现为钱币型，面积为0.25 μm2(见图9)，微裂缝随机分布于微观结构中.图10为水泥浆体中微裂缝和冰梁单元的分布.看似随机分布的微裂缝，实际上具有一定的规律性，所有的微裂缝都分布在冰梁单元的周围.这是因为在充满冰的孔隙周围的固相所承受的应力较大，而远离冰的固相所承受的应力较小.在断裂的275个梁单元中，274个梁单元的抗拉强度为0.15 GPa(表3中类型3、类型5和类型6)，这说明断裂首先发生在抗拉强度低的薄弱地带，即在外部水化产物中首先产生微裂缝.因此，由本文所提出的水泥浆体的冰冻破坏模型的模拟结果可以得出，当水泥浆体受到冰冻作用时，破坏首先发生在由水转变为冰的孔隙周围的抗拉强度低的固相水化产物中.

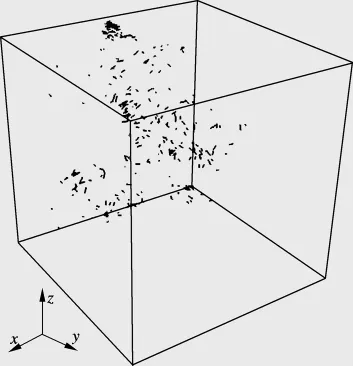
图9 微裂缝在水泥浆体中的分布

图10 微裂缝和冰单元在水泥浆体中的分布

4 结论

本文从水泥浆体的微观结构出发，把握冰在孔隙中的生长过程，将水由液态转变为固态时的体积膨胀转换为力学因素，通过三维格构结构断裂模型分析水泥浆体的内部损伤，建立了一个预测水泥浆体微观结构劣化的数值模型.以水灰比 为0.4、水化程度为0.69、边长为25 μm的普通波特兰水泥浆体的模拟结构为例，在0.5 μm/像素的条件下计算得到其孔隙率为4.7%.当温度ΔT=0.27℃时，这个模拟结构的孔隙中共有97.6%的水转变为冰.这个含有液态水、结晶态冰和固相水化产物的模拟微观结构转变为含有37.5万个梁单元的三维格构结构后，由于水转变为冰的体积膨胀9%，使得内部产生随机分布的微裂缝.从模拟结果可以看出，该模型真实反映了冰冻作用对微观结构的破坏，并且破坏首先发生在由水转变为冰的孔隙周围的抗拉强度低的固相水化产物中.

References)

［1］Metha P K，Monteiro P J M.Concrete:microstructure，properties and materials［M］.3rd ed.New York:McGraw-Hill，2006.

［2］Scherer G W.Crystallization in pores［J］.Cement and Concrete Research，1999，29(8):1347-1358.

［3］Scherer G W，Valenza J.Mechanisms of frost damage［C］//Materials Science of Concrete.Westerville，OH，USA，2005:209-246.

［4］Setzer M J.Micro-ice-lens formation in porous solid［J］.Journal of Colloid and Interface Science，2001，243(1):193-201.

［5］Liu L，Ye G，Schlangen E，et al.Modeling the internal damage of saturated cement paste due to ice crystallization exposed to low temperature［J］.Cement and Concrete Composites，2011，33(5):562-571.

［6］Promentilla M A B，Sugiyama T，Hitomi T，et al.Quantification of tortuosity in hardened cement pastes using synchrotron-based X-ray computed microtomography［J］.Cement and Concrete Research，2009，39(6):548-557.

［7］Trtik P，Münch B，Lura P.A critical examination of statistical nanoindentation on model materials and hardened cement pastes based on virtual experiments［J］.Cement and Concrete Composites，2009，31(10):705-714.

［8］van Breugel K.Simulation of hydration and formation of structure in hardening cement-based materials［D］.Delft，The Netherlands:Faculty of Civil Engineering and Geosciences，Delft University of Technology，1991.

［9］Chen H S，Stroeven P，Ye G，et al.Influence of boundary conditions on pore percolation in model cement paste ［J］.Key Engineering Materials，2006，302/303:486-492.

［10］Ye G.Experimental study and numerical simulation of the development of the microstructure and permeability of cementitious materials［D］.Delft，The Netherlands:Faculty of Civil Engineering and Geosciences，Delft University of Technology，2003.

［11］Bentz D P，Garboczi E J.Percolation of phases in a three-dimensional cement paste microstructure model［J］.Cement and Concrete Research，1991，21(2/3):325-344.

［12］Bishnoi S，Schrivener K L.A new platform for modeling the hydration of cements［J］.Cement and Concrete Research，2009，39(4):266-274.

［13］Stauffer D.Introduction to percolation theory［M］.London:Taylor and Francis，1985.

［14］Tan L.Failure mechanisms in hydrating cement particle systems［D］.Delft，The Netherlands:Faculty of Civil Engineering and Geosciences，Delft University of Technology，2007.

［15］Qian Z，Schlangen E，Ye G，et al.Prediction of mechanical properties of cement paste at microscale ［J］.Materiales de Construccion，2010，60(297):7-18.

［16］Schlangen E.Experimental and numerical analysis of fracture processes in concrete［D］.Delft，The Netherlands:Faculty of Civil Engineering and Geosciences，Delft University of Technology，1993.

［17］Bolander J E，Sukumar N.Irregular lattice model for quasistatic crack propagation［J］.Physical Review B，2005，71(9):094106-1-094106-12.

［18］Manzano H，Dolado J S，Ayuela A.Elastic properties of the main species present in Portland cement pastes［J］.Acta Materialia，2009，57(5):1666-1674.

［19］Qian Z，Ye G，Schlangen E，et al.3D lattice fracture model:application to cement paste at microscale ［J］.Key Engineering Materials，2011，452/453:65-68.

［20］Sanahuja J，Dormieux L，Chanvillard G.Modeling elasticity of a hydrating cement paste［J］.Cement and Concrete Research，2007，37(1):1427-1439.

［21］Petrovic J J.Review mechanical properties of ice and snow ［J］.Journal of Materials Science，2003，38(1):1-6.