采用离散元方法评价集料的骨架结构

陈 俊 黄晓明

(1河海大学土木与交通学院，南京210098)

(2东南大学交通学院，南京210096)

骨架密实型混合料优良的路用性能与改性沥青、纤维材料和高品质集料的使用有较大关系，更得益于其内部粗集料构成的骨架结构［1-3］.长期以来，一般认为构成沥青混合料骨架结构的是粗集料，而细集料主要起填充作用.比如，美国联邦沥青技术中心(NCAT)和我国的《公路沥青路面施工技术规范》(JTG F40—2004)就是采用干捣粗集料的方法测定粗集料间隙率VCADRC，并以沥青混合料中粗集料矿料间隙率VCAmix≤VCADRC作为骨架结构是否构成的判据［3-4］.但是，此种骨架判据是否正确，细集料是否完全不参与骨架结构受力，目前尚没有明确的依据.此外，在贝雷法中，细集料也被认为仅填充粗集料所构成骨架结构，并以0.22倍的公称最大粒径作为粗细集料的界限［5］.但是，无论是 VCAmix≤VCADRC骨架构成判据，还是贝雷法以0.22作为粗细集料的分界，都建立在集料室内试验的基础上，而室内试验并不能对混合料内部的骨架结构受力作出定量分析.因此，对于沥青混合料内部的骨架结构构成，各档集料在骨架结构内的受力特征，以及粗细集料的分界点等研究人员关心的问题，目前各类技术规范都没有作出合理的解释和说明.

作为一种新近发展起来的数值模拟方法，离散元法已经逐渐在道路材料领域得以应用.如1991年Rothenburg等利用离散元方法，研究了沥青路面的车辙问题［6］;文献［7-9］采用离散元方法研究了沥青混合料的断裂机理;文献［10-11］采用二维颗粒流程序(PFC2D)预测了沥青混合料的模量，通过室内的实际试验，验证了离散元模拟结果的正确性.Chen等［12-13］采用三维颗粒流程序(PFC3D)进行了沥青混合料各向异性和动态特性等研究.上述研究都表明，离散元在处理材料的应力不连续和大变形问题方面存在优势，尤其擅长于颗粒类材料的力学性能分析.

考虑到离散元方法的上述优势，本文采用离散元方法对单个集料颗粒进行三维不规则形状模拟;在此基础上，进行不同粒径集料逐级填充的模拟，并采集各集料颗粒与其他集料的接触点、接触力等参数，以此研究骨架结构内各档集料的受力特征和关键粒径.

1 具有级配特征的集料混合料模拟

1.1 集料颗粒的模拟

集料尤其是粗集料颗粒的不规则形状对沥青混合料宏观力学行为具有显著的影响［14］，为此，参照文献［15］关于不规则颗粒生成的研究成果，在PFC3D内生成由多个球形单元相互重叠的“Clump”，以“Clump”模拟集料颗粒的不规则形状.图1为粗集料颗粒的典型形状.

对于上述生成的任一颗粒，其体积按下式计算:

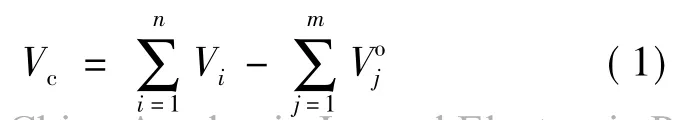
图1 典型颗粒的不规则形状

式中，n和m分别为一个集料颗粒内所包含的球形单元和球单元相互重叠的个数;Vi为集料颗粒内第i个球形单元的体积;为第j个重叠部分的体积，由下式计算:

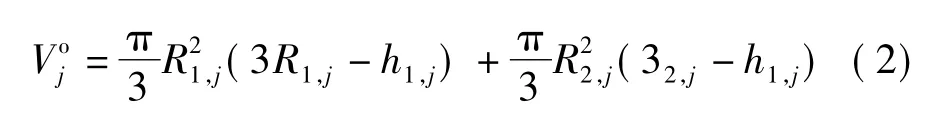
式中，R1，j和 R2，j分别为形成第 j个重叠的 2 个球形单元的半径;h1，j和 h2，j分别为2 个球形单元重叠部分球冠的高度.把式(1)和(2)编制子程序嵌入到PFC3D内可以方便地计算出各个集料颗粒的体积.在集料密度设定后，即可获得每个颗粒的质量，这为按照集料级配建立集料混合物离散元模型奠定了基础.

1.2 具有级配特征的集料混合料生成方法

在单个集料生成后，按照集料的级配和拟投放集料混合物的总质量，计算得到各档集料的质量，并按照一定算法把各档集料投放到高度为500 mm，半径为75 mm的圆柱筒中.具体投放算法是:① 按照集料粒径由大至小逐级投放.② 每投放完毕一个集料颗粒，判断该颗粒与已投放颗粒是否重叠、该颗粒是否在设定的投放空间区域内;若满足要求，则可以投放下一集料的颗粒，否则重复步骤②.③判断该颗粒投放后，该档集料质量是否达到设定的质量，若没有，则开始投放该档下一集料;若是，则开始投放粒径较小的下一档集料.图2(a)是投放到圆筒内的集料混合物，其中粒径13.2～16 mm为 2.5 kg，粒径9.50～13.2 mm 为 1.25 kg，粒径4.75～9.50 mm 为1.25 kg.

图2 集料混合物的生成

为了使得集料相互接触，本文采用先自由落体集料颗粒，后对圆筒底座施加振动荷载的方式，保证集料处于稳定接触的状态.采用的振动荷载形式如图2(b)所示，当对图2(a)所示的混合料施加自由落体和50个周期振动荷载后，骨架结构的集料混合物如图2(c)所示.

2 骨架结构受力特征的评价参数

参照Gopalakrishnan等［16］的研究，以集料混合物间隙率、各个集料的接触点数量、各接触点的接触力作为评价骨架集料受力特征的参数.

1)集料间隙率 集料混合物的矿料实体所占的体积V由下式计算:

式中，Vc，m为第m个集料的体积，可由PFC3D采集得到;p'为混合物中集料总数.集料间隙率VV可按下式计算:

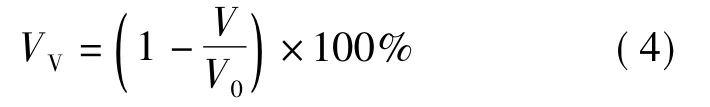
式中，V0为矿料混合物所在圆柱体的体积.

2)集料接触点和接触力 当集料混合物振动压实后，在压缩外力作用下，荷载通过集料之间的接触点相互传递.各档集料单个颗粒的平均接触点数量可由下列步骤获得:①在PFC3D内编写子程序，采集第k档集料中第l个颗粒与周围集料的接触点数量nk，l;② 根据计算第 k 档集料(该档集料共有g个颗粒)所有接触点数量;③由¯nk=nk/g，得到第k档集料单个颗粒的平均接触点数.当集料混合物上表面作用压缩荷载时，第k档集料单个颗粒接触点的平均接触力按下式计算:

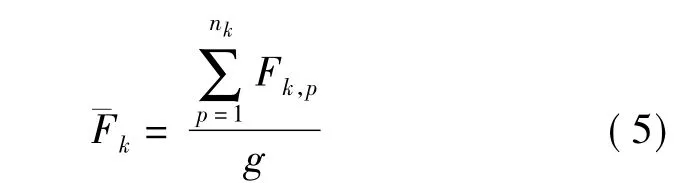
第k档集料平均接触力在所有集料接触力中所占的比例Pk，可以间接表征第k档集料在抵抗压缩荷载时的贡献率，按下式计算:

式中，Fk，p为第k档集料颗粒与周围颗粒相接触的第p个接触点;为第k档集料颗粒的平均接触力;s为集料混合物中集料档数或级数.

3 各档集料的逐级填充试验模拟

3.1 粗集料受力特征分析

考虑到混合料的级配千差万别，本文选择表1所示的典型SMA级配进行逐级填充模拟.模拟时，各种混合物的集料总质量均为3 kg.集料采用线弹性接触模型，集料弹性模量取50 GPa，摩擦系数和集料的密度分别设定为0.2和3 000 kg/m3.

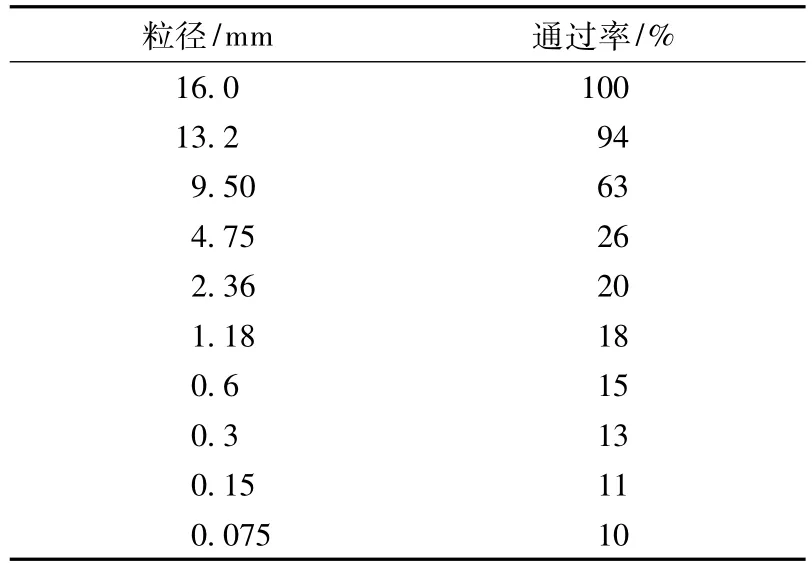
表1 用于逐级填充试验的集料级配

逐级填充的步骤为:① 把粒径13.2～16.0 mm的集料投放到高度500 mm、半径为75 mm的圆筒内，振动形成骨架1#混合物;② 把粒径9.50～13.2 mm的集料与粒径13.2～16.0 mm的集料按照表1级配混合，振动形成集料2#混合物;③ 把粒径4.75～9.50 mm的集料，按表1级配混合到粒径9.50～13.2 mm和13.2～16.0 mm混合物中，其中粒径9.50～13.2 mm和13.2～16.0 mm混合物的级配也按照表1设置，形成集料3#混合物.对于形成的集料混合物，按照本文上述介绍的方法，得到的集料间隙率、各档集料单个颗粒的平均接触数和各档集料颗粒接触力的贡献率，如表2所示.

从表2可见，集料间隙率大小的总体排序为3#＜2#＜1#，说明较细一级集料的加入可以降低矿料间隙率.当9.50～13.2 mm集料混入13.2～16.0 mm集料中形成2#混合物时，13.2～16.0 mm集料的接触点数量较1#混合物有较大程度的增大;当4.75～9.50 mm集料加入9.50～13.2 mm和13.2～16.0 mm集料混合物中形成3#混合物时，9.50～13.2 mm和13.2～16.0 mm集料接触点数量较2#也有较大程度的增大.这表明随着较细一级集料的混入，较粗级别集料的接触数都有一定程度的增加.不仅如此，横向比较同一混合物中不同粒径集料的接触点数量可以看出，较粗集料的接触点数量要多于较细集料.

表2 集料混合物的受力特征

当集料混合物上表面作用一个压缩荷载时，从PFC3D采集得到的各粒径集料接触力贡献率来看，13.2～16.0 mm，9.50 ～13.2 mm，4.75～9.50 mm三档集料中相邻两档之间受力贡献率的比值为1.09和1.2，表明较粗集料的接触力贡献率要高于较细集料的接触力.此外，当加入4.75～9.50 mm集料形成 3#混合物时，13.2～16.0 mm，9.50～13.2 mm两档集料的接触力贡献率有较大幅度的降低.表明外力作用下，较粗集料承担了较大的荷载，较细集料的加入有助于降低较粗集料的受力.

3.2 细集料的填充作用分析

按表1所示的级配，采用逐级填充的方法，可以获得9组集料混合物，为了形象地反映各档集料的作用，以集料类型为横坐标，分别以集料颗粒接触点数量和接触力贡献率为纵坐标，绘制图3.从图3(a)不难看出，当较细集料加入后，确实能够降低原有较粗集料的接触力贡献率;但是随着加入集料粒径的变小，较细集料对较粗集料的分担作用越小，当混入小于2.36 mm颗粒时这种分担作用已不大明显.另外还可以看出，即使在各档集料都存在的9#混合物中，粒径为4.75 mm以上的集料承担了85%以上的接触力贡献率，因此可以认为较粗集料在抵抗压缩荷载时发挥了主要作用，但细集料抵抗荷载的贡献也不容忽视.

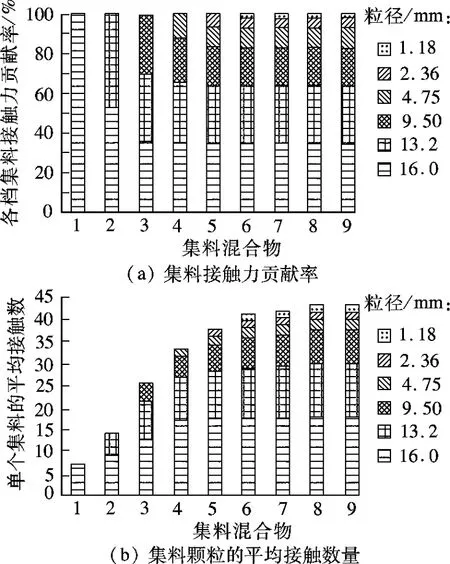
图3 各个混合物的集料接触特征

图3(b)为各类集料混合物中各档集料单个颗粒接触点数量，从图中可以看出，较细一级集料的加入可以增加原有较粗集料的接触点，尤其是加入大于4.75 mm颗粒时，这种现象尤为明显，而小于2.36 mm颗粒对集料接触点的增大作用不十分显著，当填充颗粒粒径小于1.18 mm时，颗粒填充已不能有效增加集料的接触数量.当然，上述分析都是建立在表1典型SMA混合料级配基础上的，级配和集料最大粒径变化后，集料的受力特征有待进一步研究.

3.3 关键粒径分析

以图3为基础，在考虑集料颗粒数后，本文计算了9组集料混合物的总体接触点数，由于小于1.18 mm颗粒对接触点数量的增加不明显，表3仅给出了其中的5组混合料接触点数量.从表中数据可以看出，随着细集料的加入，混合物的接触点数量有明显的提高，尤其是4.75～9.50 mm档集料加入后的3#混合物，接触点数在2#混合物的基础上增加了近2倍，且全级配混合物的接触点数量约有一半都是由于4.75～9.50 mm档集料加入后所提供的.从这个意义上来说，4.75～9.50 mm档集料是构成骨架的关键粒径.

另一方面，考虑到各组混合物是通过逐级填充形成的，各组混合物中粗集料的级配与前一组混合物的级配一致，因此各档集料逐级填充后，从集料混合物接触点数量的变化规律可以看出，接触点数量越多的混合物所能承受的压缩荷载越大.4.75～9.50 mm档集料是抵抗压缩荷载的关键粒径.因此，从增加接触点幅度的角度来看，对于公称最大粒径为13.2 mm的集料混合物，按粒径的重要程度可排列为 4.75 mm，2.36 mm，9.50 mm，1.18 mm.

表3 各组集料混合物的接触点总数

4 集料破碎试验

为了验证上述离散元模拟结果，本文进行了集料的压碎试验.试验把3 kg集料分3层捣实放入压碎值筒中，在500 kN的压力下进行压碎试验，并对压碎后的集料进行筛分试验.图4为16.0～19.0 mm，13.2 ～16 mm，9.50 ～13.2 mm，4.75 ～9.50 mm 4组集料压碎筛分后的级配.从图中可以看出，无论是16.0～19.0 mm 档集料，还是其他粒径的集料，压碎后的集料混合物中，粒径在4.75～9.50 mm的集料最多，这就表明粗集料压碎时优先破碎为4.75～9.50 mm的颗粒.

集料破碎的过程可以理解为增加骨架内接触点数量、减小大颗粒接触力贡献率、增强骨架稳定性的过程.图4所示的集料破碎规律进一步表明，在集料的破碎过程中，粗集料破碎成4.75～9.50 mm的颗粒更有利于抵抗外部荷载，保持骨架结构的稳定.这就证明了4.75～9.50 mm集料可有效地增加集料混合物内部接触点，4.75 mm颗粒是骨架构成的关键粒径.

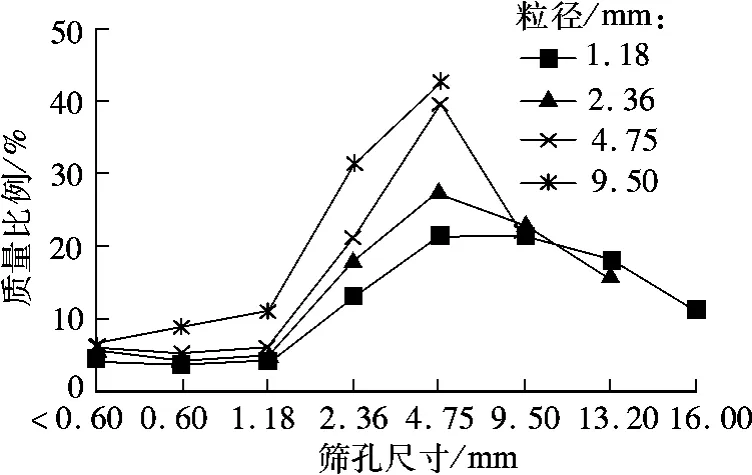
图4 破碎后各粒径集料的质量比例

5 结论

1) 在压缩荷载作用下，13.2～16.0 mm，9.50～13.2 mm，4.75～9.50 mm这三档集料中相邻两档的受力比例为1.09和1.2，混合物中颗粒粒径越大的集料，受力越大.

2)在较粗集料的混合物中添加粒径大于2.36 mm的较细集料，可以降低原有集料混合物的间隙率，增加原有粗集料的接触点，降低原有粗集料的受力;添加的较细集料越多，较粗集料接触点数量增加得越多，较粗集料的接触力贡献率越低.

3)粒径在4.75～9.50 mm的集料能够有效增加集料混合物的接触点数量，4.75 mm是组成骨架型沥青混合料的关键粒径.

References)

［1］贾渝.SMA混合料设计［J］.国外公路，1994(3):46-51.Jia Yu.Design of SMA ［J］.Journal of Foreign Highway，1994(3):46-51.(in Chinese)

［2］余叔藩.SMA路面技术在美国的发展［J］.公路，1998，44(10):21-23.Yu Shufan.The development of SMA in USA ［J］.Highway，1998，44(10):21-23.(in Chinese)

［3］Brown E R，Haddock J E.Method to ensure stone-onstone contact in stone matrix asphalt paving mixtures［J］.Journal of the Transportation Research Board，1997，1583:11-18.

［4］交通部公路科学研究所.JTG F40—2004公路沥青路面施工技术规范［S］.北京:人民交通出版社，2004.

［5］Vavrik W R，Pine W J，Carpenter S H.Aggregate blending for asphalt mix design:Bailey method［J］.Journal of the Transportation Research Board，2002，1789:146-153.

［6］Rothenburg L，Bathurst R J.Numerical simulation of idealized granular assemblies with plane elliptical particles［J］.Computers and Geotechnics，1991，11(4):315-329.

［7］Kim H，Buttlar W G.Discrete fracture modeling of asphalt concrete［J］.International Journal of Solids and Structures，2009，46(13):2593-2604.

［8］Kim H，Wagoner M P，Buttlar W G.Micromechanical fracture modeling of asphalt concrete using a single-edge notched beam test［J］.Materials and Structure，2009，42(5):677-689.

［9］Chen J，Pan T，Huang X.Discrete element modeling of asphalt concrete cracking using a user-defined threedimensional micromechanical approach［J］.Journal of Wuhan University of Technology:Materials Science Edition，2011，26(6):1215-1221.

［10］Buttlar W G，You Z P.Discrete element modeling of asphalt concrete:a micro-fabric approach［J］.Journal of the Transportation Research Board，2001，1757:111-118.

［11］You Z，Buttlar W G.Discrete element modeling to predict the modulus of asphalt concrete mixtures［J］.ASCE Journal of Materials in Civil Engineering，2004，16(2):140-146.

［12］Chen J，Pan T，Huang X.Numerical investigation into the stiffness anisotropy of asphalt concrete from a microstructural perspective［J］.Construction and Building Materials，2011，25(7):3059-3065.

［13］Chen J，Pan T，Chen J，et al.Predicting the dynamic behavior of asphalt concrete using three-dimensional discrete element method［J］.Journal of Wuhan University of Technology: MaterialsScienceEdition，2012，27(2):382-388.

［14］Pan T，Tutumluer E，Carpenter S H.Effect of coarse aggregate morphology on permanent deformation behavior of hot mix asphalt［J］.ASCE Journal of Transportation Engineering，2006，132(7):580-589.

［15］Lu M，Mcdowell G R.The importance of modeling ballast particle shape in the discrete element method［J］.Granular Matter，2007，9(1/2):69-80.

［16］Gopalakrishnan K，Shashidhar N.Structural characteristics of three-dimensional random packing of aggregates with wide size distribution［J］.International Journal of Information Technology，2006，3(3):201-208.